Аннуитет
Если, помимо начальной инвестиции, через равные периоды времени производятся дополнительные равновеликие платежи (дополнительные инвестиции), то расчет Приведенной стоимости существенно усложняется (см. статью
Аннуитет. Определяем в MS EXCEL Приведенную (Текущую) стоимость
, где приведен расчет с помощью функции
ПС()
, а также вывод альтернативной формулы).
Здесь разберем другую задачу (см.
файл примера
):
Клиент открыл вклад на срок 1 год под ставку 12% годовых с ежемесячным начислением процентов в конце месяца. Клиент также в конце каждого месяца вносит дополнительные взносы в размере 20000р. Стоимость вклада в конце срока достигла 1000000р. Какова первоначальная сумма вклада?
Решение может быть найдено с помощью функции
ПС()
:
=ПС(12%/12;12;20000;-1000000;0)
= 662 347,68р.
Аргумент
Ставка
указан за период начисления процентов (и, соответственно, дополнительных взносов), т.е. за месяц. Аргумент
Кпер
– это количество периодов, т.е. 12 (месяцев), т.к. клиент открыл вклад на 1 год.
Аргумент
Плт
– это 20000р., т.е. величина дополнительных взносов. Аргумент
Бс
– это -1000000р., т.е. будущая стоимость вклада. Знак минус указывает на направление денежных потоков: дополнительные взносы и первоначальная сумма вклада одного знака, т.к. клиент
перечисляет
эти средства банку, а будущую сумму вклада клиент
получит
от банка.
Это очень важное замечание касается всех
функций аннуитета
, т.к. в противном случае можно получить некорректный результат. Результат функции
ПС()
– это первоначальная сумма вклада, она не включает Приведенную стоимость всех дополнительных взносов по 20000р.
В этом можно убедиться подсчитав Приведенную стоимость дополнительных взносов. Всего дополнительных взносов было 12, общая сумма 20000р.*12=240000р. Понятно, что при действующей ставке 12% их Приведенная стоимость будет меньше
=ПС(12%/12;12;20000)
= -225 101,55р. (с точностью до знака). Т.к.
эти 12 платежей, сделанные в разные периоды времени, эквивалентны 225 101,55р. на момент открытия вклада, то их можно прибавить к рассчитанной нами первоначальной сумме вклада 662 347,68р. и подсчитать их общую Будущую стоимость
= БС(12%/12;12;; 225 101,55 662 347,68)
= -1000000,0р., что и требовалось доказать.
Вычисление суммы процентов, которую необходимо выплатить в промежутке между 2-мя периодами
Способ 1. Функция ОБЩПЛАТ()
Функция ОБЩПЛАТ(ставка; кол_пер; нз; нач_период; кон_период; тип)
возвращает кумулятивную (нарастающим итогом) величину процентов, выплачиваемых по займу в промежутке между двумя периодами выплат (
нач_период
и
кон_период
).
Примечание
.
Английская версия: CUMIPMT(rate, nper, pv, start_period, end_period, type) returns the CUMulative Interest paid on a loan between start_period and end_period.
Аргументы функции: Ставка – обязательный аргумент. Процентная ставка за период. Кол_пер – обязательный аргумент (кол_пер – это аргумент кпер в других функциях аннуитета, например в
ПЛТ()
). Общее количество периодов выплат.
Нз – обязательный аргумент (нз – это аргумент пс в других функциях аннуитета, например в
ПЛТ()
). Начальное значение (чаще всего – сумма кредита). Нач_период – обязательный аргумент. Номер первого периода, включенного в вычисления.
Примечание
. Убедитесь, что аргумент “Ставка” соответствуют ставке за период (период не обязательно = году). Например, при ежемесячных выплатах по 4-х летнему займу из расчета 12 процентов годовых используйте значение 12%/12 для аргумента “Ставка”.
Аргумент “Кол_пер” будет равен 4*12. При ежегодных платежах по тому же займу используйте значение 12% для аргумента “ставка” и 4 — для аргумента “Кол_пер”. При ежеквартальных платежах по тому же займу используйте значение 12%/4 для аргумента “ставка” и 4*4 — для аргумента “Кол_пер”.
Примечание
.
Функция
ОБЩПЛАТ()
возвращает значение ошибки #ЧИСЛО! если: “Ставка” ≤ 0, “кол_пер” ≤ 0 или “нз” ≤ 0, “нач_период” < 1, “кон_период” < 1 “нач_период” > “кон_период” “тип” является любым числом, отличным от 0 и 1
Альтернативная формула:
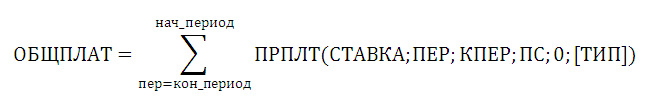
Из анализа альтернативной формулы ясно, что функция
ОБЩПЛАТ()
может использоваться, только если БС=0, т.е. когда предполагается, что по прошествии количества периодов “Кол_пер” займ полностью погашается.
Также обратите внимание, что в определении функции
ОБЩПЛАТ()
речь идет только о займе. Определить сумму, накопленную за счет процентов в случае срочного вклада, с помощью функции
ОБЩПЛАТ()
не получится (для этого см. Способ 2).
Способ 2. Функция ПРПЛТ()
Примечание
.
Английский вариант функции: IPMT(rate, per, nper, pv, [fv], [type]), т.е. Interest Payment – выплата процентов.
Чтобы вычислить сумму процентов, которые были выплачены в промежутке между двумя периодами, нужно использовать не одну, а несколько функций
ПРПЛТ()
. Например, вычислим сумму долга, выплаченную в 3-м и 4-м периоде: =ПРПЛТ(ставка; 3; кпер; пс; [бс]; [тип]) ПРПЛТ(ставка; 4; кпер; пс; [бс]; [тип])
Выражение СТРОКА(ДВССЫЛ(нач_период&”:”&кон_период)) создает
массив последовательных чисел
, например 2:3:4:5 (если нач_период=2 и кон_период=5). Функция
СУММПРОИЗВ()
суммирует результаты
ПРПЛТ()
, т.е. вышеуказанная формула эквивалентна формуле:
Расчет доходности вкладов. как сравнить вклады. расчет эффективных процентов
Для того чтобы можно было сравнивать вклады с разным способом начисления процентов, необходимо сначала привести их к «единому знаменателю». Очевидно, что главным показателем является то, сколько денег мы получим после окончания срока вклада. Рассмотрим, как посчитать эту сумму для вкладов с разным типом начисления процентов.
Пусть
Y – сумма, которую мы получим на руки при закрытии вклада.
Х – начальная сумма вклада (например, 100 000 рублей).
N – длительность вклада в годах (например, 3).
P – номинальный процент по вкладу, деленный на 100 (например 0,05).
Тогда, если проценты по вкладу выплачиваются в конце:
Подставим цифры:
Теперь представим себе, что проценты каждый год зачисляются на вклад (капитализируются).
Тогда через год у вас на вкладе будет:
Через два года:
Через 3 года:
Через N лет:
Подставим цифры:
Если капитализация процентов происходит ежеквартально, то
Если капитализация процентов происходит ежемесячно, то
Отметим, что мы здесь не учитываем то, что месяцы имеют разную длину в днях. Это не имеет принципиального значения.
Несколько сложнее обстоят дела, если проценты не капитализируются, а выплачиваются на текущий или карточный счет. Здесь уже нет возможности заранее рассчитать итоговую сумму. Всё будет зависеть от того как вы распорядитесь полученными деньгами: положите в тумбочку, потратите или положите на другой вклад. Заранее не известно под какой процент вы сможете их реинвестировать. Обычно, при сравнении вкладов принято считать, что проценты реинвестируются под тот же процент, что был не вкладе (то есть аналог капитализации). Это не совсем точно, но, увы, ничего лучшего не предложено.
Ну и, наконец, рассмотрим вариант с выплатой процентов «вперед», сразу при открытии вклада. Как правило, проценты выплачивают на текущий счет. Рассмотрим случай, когда вы полученные проценты кладете на этот же (такой же) вклад, полученные проценты на проценты тоже и так до бесконечности. Да, конечно, это «сферический конь в вакууме», реально такое получится, дай Бог одна-две итерации, но давайте вначале рассмотрим «коня».
Итак, положив сумму X, вы получите P*N*Х рублей в виде процентов
Положив на такой же вклад эти проценты, вы получите на них
Положив на такой же вклад и эти проценты, вы получите на них
И т.д. В итоге, после окончания вклада вы получите на руки:
Или
Не буду утомлять вас сложной математикой, но получившийся числовой ряд может быть заменен простой формулой (не верите – проверьте, скажем, в EXCEL). В итоге имеем:
Отметим, что эта формула представляет собой «сферического коня в вакууме». В реальности получаемая сумма будет сильно зависеть от того, как удастся реинвестировать полученный в начале вклада процент. Мне не известны прецеденты, когда расчет итоговой суммы велся по этой формуле. Обычно проценты выплачивают на текущий вклад, а для открытия или пополнения вклада установлен достаточно большой лимит. В итоге в ряде
реально удается реализовать не больше чем на 1-2 ступеньки. А потому часть полученных процентов приходится инвестировать под иной, как правило, более низкий процент. Поэтому реально в конце срока вклада получится сумма, несколько меньше, чем та, что получается по формуле. Поэтому доходность по вкладу с выплатой вперед следует признать условной.
Итак, мы получили формулы для решения прямой задачи – по проценту получить итоговую сумму на вкладе.
Однако наша задача – сравнить вклады.
Пусть:
Сравним два вклада с выплатой в конце и с ежемесячной капитализацией, которые имеют одинаковую доходность
Используем полученные выше формулы
После элементарных преобразований получаем
Аналогично
Для удобства сравнения была сделана электронная таблица, скачать которую можно здесь.
В ячейку B3 вводится номинальная ставка (указанная в условиях вклада), в ячейке A3 из списка выбирается тип начисления процентов. В одной из двух ячеек (C3 или D3) вводится продолжительность вклада в годах (C3) или днях (D3).
Затем, по одной из приведенных выше формул (в зависимости от типа начисления процентов) рассчитывается эквивалентный по доходности процент по вкладу с выплатой в конце. И, наконец, по тем же формулам, только «вывернутым наизнанку» рассчитывается процент вкладов с эквивалентной доходностью с разными типами начисления процентов.
Отметим, что точно по тому же принципу работает расчет процентов в таблице вкладов с максимальной доходностью.
———————————————————————————————————
Оглавление блога “Справочник начинающего (и не очень) инвестора”








