Выполнение расчетов с помощью финансовых функций
В группу данных операторов входит более 50 формул. Мы отдельно остановимся на десяти самых востребованных из них. Но прежде давайте рассмотрим, как открыть перечень финансового инструментария для перехода к выполнению решения конкретной задачи.
Переход к данному набору инструментов легче всего совершить через Мастер функций.
- Выделяем ячейку, куда будут выводиться результаты расчета, и кликаем по кнопке «Вставить функцию», находящуюся около строки формул.
Запускается Мастер функций. Выполняем клик по полю «Категории».
Открывается список доступных групп операторов. Выбираем из него наименование «Финансовые».
В Мастер функций также можно перейти через вкладку «Формулы». Сделав переход в неё, нужно нажать на кнопку на ленте «Вставить функцию», размещенную в блоке инструментов «Библиотека функций». Сразу вслед за этим запустится Мастер функций.
Имеется в наличии также способ перехода к нужному финансовому оператору без запуска начального окна Мастера. Для этих целей в той же вкладке «Формулы» в группе настроек «Библиотека функций» на ленте кликаем по кнопке «Финансовые».
Одним из наиболее востребованных операторов у финансистов является функция ДОХОД. Она позволяет рассчитать доходность ценных бумаг по дате соглашения, дате вступления в силу (погашения), цене за 100 рублей выкупной стоимости, годовой процентной ставке, сумме погашения за 100 рублей выкупной стоимости и количеству выплат (частота).
Именно эти параметры являются аргументами данной формулы. Кроме того, имеется необязательный аргумент «Базис». Все эти данные могут быть введены с клавиатуры прямо в соответствующие поля окна или храниться в ячейках листах Excel. В последнем случае вместо чисел и дат нужно вводить ссылки на эти ячейки.
Главной задачей функции БС является определение будущей стоимости инвестиций. Её аргументами является процентная ставка за период («Ставка»), общее количество периодов («Кол_пер») и постоянная выплата за каждый период («Плт»).
Оператор ВСД вычисляет внутреннюю ставку доходности для потоков денежных средств. Единственный обязательный аргумент этой функции – это величины денежных потоков, которые на листе Excel можно представить диапазоном данных в ячейках («Значения»).
Причем в первой ячейке диапазона должна быть указана сумма вложения со знаком «-», а в остальных суммы поступлений. Кроме того, есть необязательный аргумент «Предположение». В нем указывается предполагаемая сумма доходности. Если его не указывать, то по умолчанию данная величина принимается за 10%. Синтаксис формулы следующий:
Оператор МВСД выполняет расчет модифицированной внутренней ставки доходности, учитывая процент от реинвестирования средств. В данной функции кроме диапазона денежных потоков («Значения») аргументами выступают ставка финансирования и ставка реинвестирования. Соответственно, синтаксис имеет такой вид:
Оператор ПРПЛТ рассчитывает сумму процентных платежей за указанный период. Аргументами функции выступает процентная ставка за период («Ставка»); номер периода («Период»), величина которого не может превышать общее число периодов; количество периодов («Кол_пер»); приведенная стоимость («Пс»).
Оператор ПЛТ рассчитывает сумму периодического платежа с постоянным процентом. В отличие от предыдущей функции, у этой нет аргумента «Период». Зато добавлен необязательный аргумент «Тип», в котором указывается в начале или в конце периода должна производиться выплата. Остальные параметры полностью совпадают с предыдущей формулой. Синтаксис выглядит следующим образом:
Формула ПС применяется для расчета приведенной стоимости инвестиции. Данная функция обратная оператору ПЛТ. У неё точно такие же аргументы, но только вместо аргумента приведенной стоимости («ПС»), которая собственно и рассчитывается, указывается сумма периодического платежа («Плт»). Синтаксис соответственно такой:
Следующий оператор применяется для вычисления чистой приведенной или дисконтированной стоимости. У данной функции два аргумента: ставка дисконтирования и значение выплат или поступлений. Правда, второй из них может иметь до 254 вариантов, представляющих денежные потоки. Синтаксис этой формулы такой:
Функция СТАВКА рассчитывает ставку процентов по аннуитету. Аргументами этого оператора является количество периодов («Кол_пер»), величина регулярной выплаты («Плт») и сумма платежа («Пс»). Кроме того, есть дополнительные необязательные аргументы: будущая стоимость («Бс») и указание в начале или в конце периода будет производиться платеж («Тип»). Синтаксис принимает такой вид:
Оператор ЭФФЕКТ ведет расчет фактической (или эффективной) процентной ставки. У этой функции всего два аргумента: количество периодов в году, для которых применяется начисление процентов, а также номинальная ставка. Синтаксис её выглядит так:
Нами были рассмотрены только самые востребованные финансовые функции. В общем, количество операторов из данной группы в несколько раз больше. Но и на данных примерах хорошо видна эффективность и простота применения этих инструментов, значительно облегчающих расчеты для пользователей.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Лабораторная работа № 4. некоторые финансовые функции excel
Работа с финансовыми функциями в MS Excel предполагает использование следующей методики:
1. Подготовить на рабочем листе значения основных аргументов функции
2. Перейти к ячейке в которую вводиться формула, использующая встроенную финансовую функцию
3. Вызвать мастер функций и в списке финансовых функций выбрать необходимую финансовую функцию.
4. Если аргумент финансовой функции является результатом расчета другой вложенной функции, используйте повторный вызов мастера функций для данного аргумента
5. После ввода всех аргументов нажмите кнопку ОК и MS Excel произведет расчет по формуле.
При задании аргументов для финансовых функций необходимо помнить следующее:
− Все аргументы, означающие расходы денежных средств (например, ежегодные платежи), представляются отрицательными числами, а аргументы, означающие поступления, (например, дивиденды) – положительными;
− Все даты, как аргументы функции имеют числовой формат
− Для логических аргументов используются константы ИСТИНА или ЛОЖЬ, либо функции категории Логические
− Каждый аргумент должен находиться на своем месте. Если аргументы пропускаются, то следует поставить соответствующее число разделительных знаков.
Задание №1.
Определить величину основного платежа за четвертый год, если выдана ссуда размером 1 000 000 000 сроком на 5 лет под 12% годовых.
Для основных платежей по займу, который погашается равными платежами в конце или в начале каждого расчетного периода используется функция ОСПЛТ, которая возвращает величину платежа в погашение основной суммы по инвестиции за данный период на основе постоянства периодических платежей и постоянства процентной ставки.
ОСПЛТ(Ставка, Период, Кпер, Пс Бс)
Ставка — процентная ставка за период.
Период — задает период, значение должно быть в интервале от 1 до «кпер».
Кпер — общее число периодов платежей по аннуитету. Например, если получена ссуда на 4 года под автомобиль и делаются ежемесячные платежи, то ссуда имеет 4*12 (или 48) периодов. В качестве значения аргумента кпер в формулу нужно ввести число 48.
Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей.
Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0 (будущая стоимость займа, например, равна 0). Например, если предполагается накопить 50000 руб. для оплаты специального проекта в течение 18 лет, то 50 000 руб. это и есть будущая стоимость. Можно сделать предположение о сохранении заданной процентной ставки и определить, сколько нужно откладывать каждый месяц.
Ввод данных и расчеты производятся в соответствии с рисунком
Задание №2.
Рассчитать 20-летнюю ипотечную ссуду со ставкой 10% годовых при начальном взносе 25% и ежемесячной (ежегодной) выплате.
Для вычисления величины постоянной периодической выплаты ренты (например, регулярных платежей по займу) при постоянной процентной ставке используется функция ПЛТ, которая возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянства процентной ставки.
ПЛТ(Ставка; Кпер; Бс; Пс; Тип).
Ставка — процентная ставка по ссуде.
Кпер — общее число выплат по ссуде.
Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой.
Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (нолю), т. е. для займа, например, значение бс равно 0.
Тип — число 0 (ноль) или 1, обозначающее, когда должна производиться выплата.
В нашем случае функция ПЛТ имеет вид:
ПЛТ(10%/12;20*12;-(350000*(1-25%))) – ежемесячные выплаты;
ПЛТ(10%;20;-(350000*(1-25%))) – ежегодные выплаты.
Решение задачи приведено на рисунках.
Задание №3.
Определить, какая сумма окажется на счете, если 52000 руб. положены на 20 лет под 11% годовых. Проценты начисляются ежемесячно.
Для расчета будущей стоимости единой суммы вклада используются сложные проценты, а расчетная формула основана на функции БС, которая возвращает будущую стоимость инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постянной процентной ставки.
Ставка — процентная ставка за период.
Кпер — общее число периодов платежей по аннуитету.
Плт — выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно аргумент «плт» состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если он опущен, аргумент «пс» является обязательным.
Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент «пс» опущен, предполагается значение 0. В этом случае аргумент «плт» является обязательным.
Тип — число 0 или 1, обозначающее срок выплаты. Если аргумент «тип» опущен, предполагается значение 0.
Для нашей задачи функция БС примет вид:
Решение задачи приведено на рисунке, а формула для расчета ячейки В30:
Задание №4.
Ожидается, что ежегодные доходы от реализации проекта составят 54000000 руб. Рассчитать срок окупаемости проекта, если инвестиции к началу поступления доходов составят 140000000 руб., а норма дисконтирования 7,67.
Для определения срока платежа используется функция КПЕР, которая возвращает общее количество периодов выплаты для инвестиции на основе периодических постоянных выплат и постоянной процентной ставки.
Ставка — процентная ставка за период.
Плт — выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно платеж состоит из основного платежа и платежа по процентам и не включает налогов и сборов.
Пс — приведенная к текущему моменту стоимость, т. е. общая сумма, которая на текущий момент равноценна ряду будущих платежей.
Бс — значение будущей стоимости, т. е. желаемого остатка средств после последней выплаты. Если аргумент «бс» опущен, предполагается, что он равен 0 (например, бс для займа равна 0).
Тип — число 0 или 1, обозначающее срок выплаты.
В нашей задаче функция выглядит следующим образом:
Задание №5.
Облигация номиналом 200000 руб. выпущена на 7 лет. Предусматривается следующий порядок начисления процентов: в первый год начисляется 11%,последующие три года – по 16%, в оставшиеся три года по 20%. Рассчитать будущую (наращенную) стоимость облигации по сложной процентной ставке.
Для расчета наращенной стоимости облигации по сложной процентной ставке используется функция БЗРАСПИС, которая возвращает будущую стоимость первоначальной основной суммы после применения ряда (плана) ставок сложных процентов. Функция БЗРАСПИС используется для вычисления будущей стоимости инвестиции с переменной процентной ставкой.
Первичное — стоимость инвестиции на текущий момент.
План — массив применяемых процентных ставок.
Решение приведено на рисунке
Формула для расчета примет следующий вид:
Задание №6.
Затраты по проекту составят 600 млн. руб. Ожидаемые доходы в течение последующих 5 лет составят, соответственно, 50, 100,300,200, 300 млн. руб. Оценить экономическую целесообразность проекта по скорости оборота инвестиций, если рыночная норма дохода 15%.
Для вычисления внутренней скорости оборота инвестиции (внутренней нормы доходности) используется функция ВСД, Возвращает внутреннюю ставку доходности для ряда потоков денежных средств представленных их численными значениями. В отличие от аннуитета, денежные суммы в пределах этих потоков могут колебаться.
Однако обязательным условием является регулярность поступлений (например, ежемесячных или ежегодных). Внутренняя ставка доходности — это процентная ставка, принимаемая для инвестиции, состоящей из платежей (отрицательные величины) и доходов (положительные величины), которые имеют место в следующие друг за другом и одинаковые по продолжительности периоды.
Значения — массив или ссылка на ячейки, содержащие числа, для которых требуется подсчитать внутреннюю ставку доходности.
Значения должны содержать по крайней мере одно положительное и одно отрицательное значение.
В функции ВСД для интерпретации порядка денежных выплат или поступлений используется порядок значений. Убедитесь, что значения выплат и поступлений введены в нужном порядке.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, такие значения игнорируются.
Предположение — величина, предположительно близкая к результату ВСД.
В нашем случае функция для решения задачи использует только аргумент Значения, один из которых обязательно отрицателен. Если внутренняя скорость оборота инвестиций будет больше рыночной нормы доходности, то проект считается экономически целесообразным. В противном случае проект должен быть отвергнут.
Для принятия решения о экономической целесообразности проекта используйте логическую функцию ЕСЛИ:
Решение приведено на рисунке:
Задание №7.
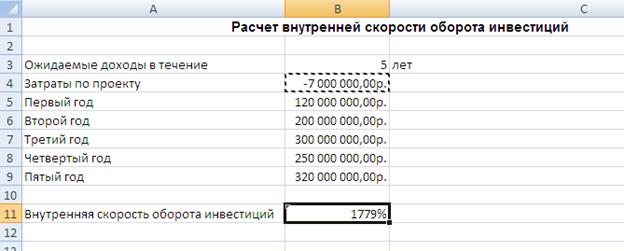
Предполагается, что доходы по проекту в течение 5 лет составят 120000000 руб., 200000000., 300000000 руб., 250000000 руб., 320000000 руб. Определить первоначальные затраты на проект, чтобы обеспечить скорость оборота 12%.
Расчет внутренней скорости оборота инвестиций производится с помощью функции ВСД. Ввод исходных данных производиться в соответствии с рисунком:
Далее, на вкладке Данные в группе Средства обработки данных выберите команду Анализ условия, а затем выберите в списке пункт Подбор параметра. Находим величину первоначальных затрат на проект, обеспечивающих скорость обороты инвестиций в 12%:
Перечень финансовых функций:
АМОРУВ — возвращает величину амортизации для каждого периода.
НАКОПДОХОД — данная функция возвращает накопленный процент по ценным бумагам с периодической выплатой процентов.
НАКОПДОХОДПОГАШ — возвращает накопленный процент по ценным бумагам, процент по которым выплачивается в срок погашения.
АМОРУМ — возвращает величину амортизации для каждого периода.
ДНЕЙКУПОНДО — возвращает количество дней от начала действия купона до даты соглашения.
ДНЕЙКУПОН — вычисляет число дней в периоде купона, содержащем дату расчета.
ДНЕЙКУПОНПОСЛЕ — возвращает число дней от даты расчета до срока следующего купона.
ДАТАКУПОНДО — возвращает число, представляющее дату следующего купона от даты соглашения.
ЧИСЛКУПОН — возвращает количество купонов, которые могут быть оплачены между датой соглашения и датой вступления в силу, округленное до ближайшего целого купона.
ОБЩПЛАТ — вычисляет кумулятивную (нарастающим итогом) величину процентов, выплачиваемых по займу в промежутке между двумя периодами выплат. exсel финансовый электронный таблица
ОБЩДОХОД — вычисляет кумулятивную (нарастающим итогом) сумму, выплачиваемую в погашение основной суммы займа в промежутке между двумя периодами.
ФУО — определяет величину амортизации актива для заданного периода, рассчитанную методом фиксированного уменьшения остатка.
ДДОБ — определяет значение амортизации актива за данный период, используя метод двойного уменьшения остатка или иной явно указанный метод.
СКИДКА — определяет ставку дисконтирования (норму скидки) для ценных бумаг.
РУБЛЬ.ДЕС — преобразует цену в рублях, представленную в виде дроби, в цену в рублях, выраженную десятичным числом. Функция РУБЛЬ.ДЕС используется для преобразования дробных значений денежных сумм, например стоимости ценных бумаг, в десятичное число.
РУБЛЬ.ДРОБЬ — преобразует цену в рублях, выраженную десятичным числом, в цену в рублях, представленную в виде дроби. Функция РУБЛЬ.ДРОБЬ используется для преобразования десятичных чисел, например стоимости ценных бумаг, в дробные цены.
ДЛИТ — находит ежегодную продолжительность действия ценных бумаг с периодическими выплатами по процентам.
ЭФФЕКТ — определяет эффективную (фактическую) годовую процентную ставку, если заданы номинальная годовая процентная ставка и количество периодов в году, за которые начисляются сложные проценты.
ЭФФЕКТ вычисляется следующим образом:
БС — вычисляет будущую стоимость инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постоянной процентной ставки.
БЗРАСПИС — вычисляет будущее значение начального вклада при изменяющихся сложных процентных ставках.
ИНОРМА — определяет ставку доходности полностью обеспеченной ценной бумаги.
ПРПЛТ — определяет сумму платежей процентов по инвестиции за данный период на основе постоянства сумм периодических платежей и постоянства процентной ставки.
ВСД — вычисляет внутреннюю ставку доходности (отдачи) для серии потоков денежных средств.
ПРОЦПЛАТ — вычисляет проценты, выплачиваемые за определенный инвестиционный период.
МДЛИТ — определяет модифицированную длительность Маколея для ценных бумаг с предполагаемой номинальной стоимостью 100 рублей.
МВСД — определяет внутреннюю ставку доходности, при которой положительные и отрицательные денежные потоки имеют разную ставку.
НОМИНАЛ — определяет номинальную годовую процентную ставку.
КПЕР — определяет общее количество периодов выплаты для инвестиции на основе периодических постоянных выплат и постоянной процентной ставки.
ЧПС — определяет величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также последовательность будущих выплат (отрицательные значения) и поступлений (положительные значения).
ЧПС аналогична функции ПС (текущее значение). Основное различие между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В функции ЧПС денежные взносы могут быть переменной величиной, тогда как в функции ПС они должны быть постоянными на протяжении всего периода инвестиции.
ЦЕНАПЕРВНЕРЕГ — находит цену за 100 рублей нарицательной стоимости ценных бумаг с нерегулярным первым периодом.
ДОХОДПЕРВНЕРЕГ — находит доход по ценным бумагам с нерегулярным (коротким или длинным) первым периодом.
ЦЕНАПОСЛНЕРЕГ — определяет цену за 100 рублей нарицательной стоимости ценных бумаг для нерегулярного (короткого или длинного) последнего периода купона.
ДОХОДПОСЛНЕРЕГ — определяет доход по ценным бумагам с нерегулярным последним периодом.
ПЛТ — Вычисляет величину выплаты по ссуде за один период.
ОСПЛТ — Вычисляет величину выплат на основной капитал для вклада в заданный период.
ЦЕНА — вычисляет цену за 100 рублей нарицательной стоимости ценных бумаг, по которым производится периодическая выплата процентов.
ЦЕНАПОГАШ — вычисляет цену за 100 рублей номинальной стоимости ценных бумаг, по которым процент выплачивается в срок погашения.
ЦЕНАСКИДКА — определяет цену за 100 рублей номинальной стоимости ценных бумаг, на которые сделана скидка.
ПС — определяет приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат. Например, в момент займа его сумма является приведенной (нынешней) стоимостью для заимодавца.
СТАВКА — определяет процентную ставку по аннуитету за один период
ПОЛУЧЕНО — вычисляет сумму, полученную в срок вступления в силу полностью обеспеченных ценных бумаг.
АПЛ — определяет величину амортизации актива за один период, рассчитанную линейным методом.
АСЧ — определяет величину амортизации актива за данный период, рассчитанную по сумме чисел лет срока полезного использования.
РАВНОКЧЕК — вычисляет эквивалентный облигации доход по казначейскому векселю.
ЦЕНАКЧЕК — вычисляет цену на 100 рублей номинальной стоимости для казначейского векселя.
ЦЕНАКЧЕК вычисляется следующим образом:
ДОХОДКЧЕК — вычисляет доходность по казначейскому векселю.
ПУО — определяет величину амортизации актива для любого выбранного периода, в том числе для частичных периодов, с использованием метода двойного уменьшения остатка или иного указанного метода.
ЧИСТВНДОХ — вычисляет внутреннюю ставку доходности запланированных непериодических денежных потоков.
ЧИСТНЗ — вычисляет чистую текущую стоимость инвестиции, вычисляемую на основе ряда поступлений наличных, которые не обязательно являются периодическими.
Функция ЧИСТНЗ вычисляется следующим образом:
ДОХОД — вычисляет доходность ценных бумаг, по которым производятся периодические выплаты процентов. Функция ДОХОД используется для вычисления доходности облигаций.
ДОХОДСКИДКА — вычисляет годовую доходность по ценным бумагам, на которые сделана скидка.
ДОХОДПОГАШ — определяет годовую доходность ценных бумаг, по которым проценты выплачиваются при наступлении срока погашения.
Расчет сложных процентов
Вот некоторые банковские опции по депозитам.
Вклады с капитализацией. Как мы уже рассмотрели, вклады с начислением процентов поэтапно внутри срока называются вкладами с капитализацией. Периодичность капитализации может быть разная, обычно — раз в месяц, но бывает ежедневная или раз в квартал.
Если банк капитализирует проценты по вкладу — начисляет и добавляет их к сумме депозита, при равных номинальных ставках такой вариант будет выгоднее, чем при начислении процентов в конце срока.
Рассмотрим варианты начисления процентов — от ежедневного до одного раза в квартал. Во всех случаях будем считать, что вы открыли депозит на 100 000 Р под 4,8% годовых на 1 год.
Ежедневная капитализация. Каждый день банк начисляет проценты и добавляет их к сумме вклада.
Упрощенный расчет будет выглядеть так.
Проценты за первый день: 100 000 × 4,8% / 365 = 13,15 Р — эту сумму банк добавит к сумме вклада по истечении первого дня.
За второй день: (100 000 13,15) × 4,8% / 365 = 13,15 Р.
За третий день: (100 000 13,15 13,15) × 4,8% / 365 = 13,16 Р.
С каждым днем сумма, на которую начисляются проценты, будет расти. Соответственно, и процентов каждый месяц будет начисляться больше.
Через год у вас на счете будет 104 916,73 Р. Эффективная ставка составит 4,92% годовых.
Ежемесячная капитализация. Каждый месяц банк будет начислять проценты и добавлять их к сумме вклада.
Упрощенный расчет будет выглядеть так.
Через год у вас на счете будет 104 907,02 Р. Эффективная ставка составит 4,91%.
Ежеквартальная капитализация. Проценты начисляются раз в три месяца. Упрощенный расчет будет выглядеть так.
Через год у вас на счете будет 104 887,09 Р. Эффективная ставка составит 4,89%.
Вклады с пополнением. Если по условиям договора вклад можно пополнять — вносить дополнительные средства, — с момента внесения процент начисляется на общую сумму.
Пример: вы открыли счет на 100 000 Р под 4,8% годовых на 1 год с возможностью пополнения, а через полгода внесли еще 50 000 Р. При годовой ставке 4,8% за полгода банк начислит 2,4% от суммы депозита. Рассчитаем процентные начисления за каждые полгода отдельно.
Без учета капитализации сумма процентных начислений составит 6 000 Р. Вкладчик в этом случае получает фиксированный процент от вложенных денег, поэтому эффективная ставка здесь не меняется — 4,8% годовых.
Если вклад с капитализацией, для вычисления эффективной процентной ставки можно отдельно рассчитать периоды до и после пополнения — как будто это два разных депозита. Эффективная ставка у вкладов будет другой из-за изменения длительности.
где:
- СО — это средний остаток по счету в течение всего срока, как если бы вы клали деньги на беспроцентный депозит;
- Д — общая длительность вклада в годах.
Это и есть смысл эффективной ставки: она показывает, под какой процент нужно вложить средний остаток по счету, чтобы получить те же проценты за тот же срок.
Вклады с частичным снятием. Иногда по условиям договора банк разрешает снимать со счета часть средств, которые лежат на депозите. При этом проценты с момента открытия депозита до момента снятия не теряются.
Пример: вы открыли депозит на 100 000 Р под 4,8% годовых на 1 год с возможностью частичного снятия, а через полгода сняли 50 000 Р. При годовой ставке 4,8% за полгода банк начислит 2,4% от суммы вклада. Рассчитаем проценты за каждые полгода отдельно.
Без капитализации сумма процентов составит 3600 Р. Эффективная процентная ставка без ежемесячной капитализации — те же 4,8%.
Расчет эффективной ставки с капитализацией можно произвести аналогично вкладу с пополнением.
Таблица расчета процентов по вкладу
Предположим, вы решили положить на депозит в банк определенную сумму денег. Естественно, вы должны рассчитать, какую сумму с учетом процентов получите через определенное время. В расчетах необходимо учесть процентную ставку по депозиту и срок размещения вклада.
На основе имеющейся таблицы умножения создадим таблицу для автоматического расчета данной суммы. Область ввода таблицы должна содержать следующие управляющие параметры:
- первоначальную сумму вклада;
- начальное значение процентной ставки по депозиту и шаг ее изменения;
- начальное значение периода времени и шаг его изменения.
Процентные ставки будут располагаться в столбце Процент области вычислений, а периоды времени — в строке, озаглавленной как Годы. В области вычислений должны отображаться суммы, величина которых зависит от срока размещения вклада и процентной ставки (рис. 3.14 и 3.15).
Мы предполагаем, что процент по депозиту сложный и начисляется в конце года (то есть период капитализации равен одному году). В каждом следующем году расчет процентов производится для суммы, положенной на депозит, плюс проценты, начисленные за предыдущий год.
Сумма вклада на конец периода рассчитывается по такой формуле:
где Р0 — сумма, размещенная на депозите, r — ставка по депозиту, n — число периодов (лет).
Рис. 3.14. Фрагмент таблицы для расчета суммы на депозита (с формулами)
Рис 3.15. Таблица для расчета суммы на депозите (с числовыми значениями)
Нам кажется, что у вас не возникнет проблем с оформлением столбцов и строк, содержащих исходные данные для расчета. Вам требуется вставить две строки (после строк 2 и 8) и ввести имена и значения параметров в область ввода. А вот процесс создания основной расчетной формулы мы опишем более подробно. Выделите диапазон В10:К19 и введите в ячейку В10 формулу для расчета, выполнив следующие действия:
- Введите знак равенства, выделите ячейку D2 и нажатиями функциональной клавиши [F4] задайте абсолютную ссылку.
- Введите знак «*» (умножить), круглую открывающую скобку, цифру 1 и знак « ».
- Выделите ячейку А10 и три раза нажмите функциональную клавишу [F4] (будет создана абсолютная ссылка на имя столбца), затем введите круглую закрывающую скобку.
- Переключитесь на английский шрифт и введите знак возведения в степень «/» путем нажатия комбинации клавиш [Shift 6].
- Выделите ячейку В9 и дважды нажмите функциональную клавишу [F4] (будет создана абсолютная ссылка на номер строки). Затем введите круглую открывающую скобку.
- Завершите ввод формулы нажатием комбинации клавиш [Ctrl Enter].
На создание таблицы уходит около одной минуты. В отличие от статической таблицы она позволяет изменять сумму, ставки депозита и вычислять результат для разных временных периодов.
Финансовые функции (справка)
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2022 означает, что данная функция доступна в выпуске Excel 2022 и всех последующих версиях.
Возвращает накопленный процент по ценным бумагам с периодической выплатой процентов.
Возвращает накопленный процент по ценным бумагам, процент по которым выплачивается в срок погашения.
Возвращает величину амортизации для каждого учетного периода, используя коэффициент амортизации.
Возвращает величину амортизации для каждого учетного периода.
Возвращает количество дней от начала действия купона до даты соглашения.
Возвращает количество дней в периоде купона, который содержит дату расчета.
Возвращает количество дней от даты расчета до срока следующего купона.
Возвращает порядковый номер даты следующего купона после даты соглашения.
Возвращает количество купонов между датой соглашения и сроком вступления в силу.
Возвращает порядковый номер даты предыдущего купона до даты соглашения.
Возвращает кумулятивную (нарастающим итогом) величину процентов, выплачиваемых по займу в промежутке между двумя периодами выплат.
Возвращает кумулятивную (нарастающим итогом) сумму, выплачиваемую в погашение основной суммы займа в промежутке между двумя периодами.
Возвращает величину амортизации актива для заданного периода, рассчитанную методом фиксированного уменьшения остатка.
Возвращает величину амортизации актива за данный период, используя метод двойного уменьшения остатка или иной явно указанный метод.
Возвращает ставку дисконтирования для ценных бумаг.
Преобразует цену в рублях, выраженную в виде дроби, в цену в рублях, выраженную десятичным числом.
Преобразует цену в рублях, выраженную десятичным числом, в цену в рублях, выраженную в виде дроби.
Возвращает продолжительность Маколея для ценных бумаг, по которым выплачивается периодический процент.
Возвращает фактическую (эффективную) годовую процентную ставку.
Возвращает будущую стоимость инвестиции.
Возвращает будущее значение первоначальной основной суммы после применения ряда (плана) ставок сложных процентов.
Возвращает процентную ставку для полностью инвестированных ценных бумаг.
Возвращает проценты по вкладу за данный период.
Возвращает внутреннюю ставку доходности для ряда потоков денежных средств.
Вычисляет выплаты за указанный период инвестиции.
Возвращает модифицированную продолжительность Маколея для ценных бумаг с предполагаемой номинальной стоимостью 100 рублей.
Возвращает внутреннюю ставку доходности, при которой положительные и отрицательные денежные потоки имеют разные значения ставки.
Возвращает номинальную годовую процентную ставку.
Возвращает общее количество периодов выплаты для инвестиции.
Возвращает чистую приведенную стоимость инвестиции, основанной на серии периодических денежных потоков и ставке дисконтирования.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг с нерегулярным (коротким или длинным) первым периодом купона.
Возвращает доход по ценным бумагам с нерегулярным (коротким или длинным) первым периодом купона.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг с нерегулярным (коротким или длинным) последним периодом купона.
Возвращает доход по ценным бумагам с нерегулярным (коротким или длинным) последним периодом купона.
ПДЛИТ 
Возвращает количество периодов, необходимых инвестиции для достижения заданного значения.
Возвращает регулярный платеж годичной ренты.
Возвращает платеж с основного вложенного капитала за данный период.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, по которым выплачивается периодический процент.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, на которые сделана скидка.
Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, по которым процент выплачивается в срок погашения.
Возвращает приведенную (к текущему моменту) стоимость инвестиции.
Возвращает процентную ставку по аннуитету за один период.
Возвращает сумму, полученную к сроку погашения полностью инвестированных ценных бумаг.
ЭКВ.СТАВКА 
Возвращает эквивалентную процентную ставку для роста инвестиции.
Возвращает величину амортизации актива за один период, рассчитанную линейным методом.
Возвращает величину амортизации актива за данный период, рассчитанную методом суммы годовых чисел.
Возвращает эквивалентный облигации доход по казначейскому векселю.
Возвращает цену за 100 рублей номинальной стоимости для казначейского векселя.
Возвращает доходность по казначейскому векселю.
Возвращает величину амортизации актива для указанного или частичного периода при использовании метода сокращающегося баланса.
Возвращает внутреннюю ставку доходности для графика денежных потоков, не обязательно носящих периодический характер.
Возвращает чистую приведенную стоимость для денежных потоков, не обязательно носящих периодический характер.
Возвращает доход по ценным бумагам, по которым производятся периодические выплаты процентов.
Возвращает годовой доход по ценным бумагам, на которые сделана скидка (например, по казначейским векселям).
Возвращает годовую доходность ценных бумаг, по которым процент выплачивается в срок погашения.
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.








