- Компаундная основа
- Инвестирование: ежемесячные вклады
- Периодическое компаундирование
- Приведение в сопоставимый вид разновременных затрат и результатов: дисконтирование, компаундирование. — мегалекции
- Пример выплаты ипотеки
- Примерная формула ежемесячного платежа
- Сила интереса
- Точная формула ежемесячного платежа
Компаундная основа
Чтобы преобразовать процентную ставку с одной основы начисления на другую основу начисления процентов, используйте
- р2знак равно[(1 р1п1)п1п2-1]п2,{ Displaystyle r_ {2} = left [ left (1 { frac {r_ {1}} {n_ {1}}} right) ^ { frac {n_ {1}} {n_ {2} }} – 1 right] {n_ {2}},}
где
r 1 – процентная ставка с частотой начисления n 1 , а
r 2 – процентная ставка с частотой начисления n 2 .
Когда проценты непрерывно начисляются , используйте
- δзнак равноппер(1 рп),{ displaystyle delta = n ln { left (1 { frac {r} {n}} right)},}
где
– процентная ставка на основе непрерывного начисления сложных процентов, а
r – заявленная процентная ставка с частотой начисления сложных процентов n .
δ{ displaystyle delta}
Инвестирование: ежемесячные вклады
Учитывая основной (начальный) депозит и повторяющийся депозит, общий доход от инвестиций можно рассчитать через сложный процент, полученный за единицу времени. При необходимости проценты по дополнительным единовременным и повторяющимся депозитам также могут быть определены по той же формуле (см. Ниже).
- п{ displaystyle P} = Основной депозит
- р{ displaystyle r} = Норма прибыли (ежемесячно)
- M{ displaystyle M} = Ежемесячный депозит и
- т{ displaystyle t} = Время в месяцах
Сложные проценты по каждому депозиту составляют:
- M′знак равноM(1 р)т{ Displaystyle М ‘= М (1 г) ^ {т}}
и добавление всех повторяющихся вкладов за весь период t (i звездочек на 0, если депозиты начинаются с инвестирования основной суммы; i звездочек на 1, если депозиты начинаются в следующем месяце):
- M′знак равно∑язнак равно0т-1M(1 р)т-я{ displaystyle M ‘= sum _ {я = 0} ^ {t-1} {M (1 r) ^ {ti}}}
распознавая геометрический ряд : и применяя формулу замкнутой формы (обыкновенное отношение :), получаем:
M′знак равноM∑язнак равно0т-1(1 р)т1(1 р)я{ displaystyle M ‘= M sum _ {я = 0} ^ {t-1} (1 r) ^ {t} { frac {1} {(1 r) ^ {i}}}}1/(1 р){ displaystyle 1 / (1 r)}
- п′знак равноM(1 р)т-1р п(1 р)т{ displaystyle P ‘= M { frac {(1 r) ^ {t} -1} {r}} P (1 r) ^ {t}}
Если происходят два или более типа депозитов (повторяющиеся или разовые), полученная сложная стоимость может быть представлена как
- Vалтыезнак равноM(1 р)т-1р п(1 р)т k(1 р)т-Икс-1р C(1 р)т-у{ displaystyle Value = M { frac {(1 r) ^ {t} -1} {r}} P (1 r) ^ {t} k { frac {(1 r) ^ { tx} -1} {r}} C (1 r) ^ {ty}}
где C – каждая единовременная выплата, а k – ежемесячные повторяющиеся депозиты, соответственно, а x и y – разницы во времени между новым депозитом и общим периодом t, моделируемым.
Практическая оценка для обратного расчета нормы прибыли, когда точная дата и сумма каждого повторяющегося депозита неизвестны, формула, которая предполагает единый повторяющийся ежемесячный депозит в течение периода, выглядит следующим образом:
- рзнак равно(п′-п-∑Mп ∑M/2)1/т{ displaystyle r = left ({ frac {P’-P- sum {M}} {P sum {M} / 2}} right) ^ {1 / t}} Или рзнак равно(п′-∑M/2п ∑M/2)1/т-1{ displaystyle r = left ({ frac {P ‘- sum {M} / 2} {P sum {M} / 2}} right) ^ {1 / t} -1}
Периодическое компаундирование
Общая накопленная стоимость, включая основную сумму плюс начисленные проценты , определяется по формуле:
п{ displaystyle P}я{ displaystyle I}
- п′знак равноп(1 рп)пт{ displaystyle P ‘= P left (1 { frac {r} {n}} right) ^ {nt}}
куда:
- P – исходная основная сумма
- P ‘ – новая основная сумма
- r – номинальная годовая процентная ставка
- n – частота сложения
- t – общий период времени, в течение которого начисляются проценты (выражается с использованием тех же единиц времени, что и r , обычно в годах).
Общая полученная сумма сложных процентов представляет собой окончательное значение за вычетом первоначальной основной суммы:
- язнак равноп(1 рп)пт-п{ displaystyle I = P left (1 { frac {r} {n}} right) ^ {nt} -P}
Приведение в сопоставимый вид разновременных затрат и результатов: дисконтирование, компаундирование. — мегалекции
Согласно основополагающим принципам экономики разновременные затраты точно так же, как и полученные результаты, неравноценны во времени. Т.е. один рубль сегодня значит больше, чем тот же один рубль полученный или затраченный через год.
Это имеет место не только из-за инфляции, но и вследствие того, что денежные средства, вовлеченные в хозяйственный оборот, приносят определенный доход.
Поэтому для суммирования реальных денежных средств по потоку за какой-либо период они должны быть предварительно приведены к сопоставимому виду – к единому моменту времени.
Такими моментами приведения могут быть или начальный или конечный шаг расчетного периода.
| Процедура приведения к конечному моменту осуществляется путем умножения текущих величин потока на шаге – m – на коэффициент компаундирования, отражающий темп приращения капитала при использовании денежных средств в хозяйственном обороте. Эта процедура называется компаундированием. |
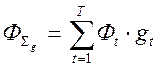 , (10)
, (10)
где 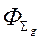 – суммарный компаундированный поток;
– суммарный компаундированный поток;
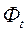 – текущая величина потока в году t;
– текущая величина потока в году t;
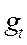 – коэффициент компаундирования.
– коэффициент компаундирования.
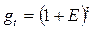 задается по формуле сложных процентов, (11)
задается по формуле сложных процентов, (11)
где Е – норма приращения капитала или приемлемая для инвестора норма дохода.
| Процедура приведения потока к начальному периоду проводится путем умножения этих же текущих величин потока на коэффициент дисконтирования, учитывающий уменьшение значимости денежного потока при его отдалении во времени. Такая процедура называется дисконтированием. |
Суммарный дисконтированный поток рассчитывается:
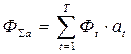 , (12)
, (12)
где  – коэффициент дисконтирования для года t.
– коэффициент дисконтирования для года t.
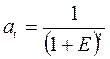 . (13)
. (13)
Здесь Е – норма дисконта по содержанию то же, что и в формуле (11).
Если приведение потока осуществляется к первому году, показатель степени принимает выражение (t-1).
В формулах (11) и (13) фигурирует одна и та же величина Е, что определяет единое по последствиям экономическое содержание процедуры компаундирования и дисконтирования.
Действительно, если в первом году мы располагаем 100 рублями, то при Е = 0,1 к концу второго года они составят  рублей, а 110 рублей второго года с позиции сегодняшнего дня составят:
рублей, а 110 рублей второго года с позиции сегодняшнего дня составят:
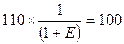 руб.
руб.
Пример. Влияние уровня нормы дохода на суммарный дисконтированный поток.
Определим суммарный дисконтированный поток 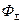 для параметров, указанных в таблице. Расчетный период Т равен 5 годам.
для параметров, указанных в таблице. Расчетный период Т равен 5 годам.
Таблица 2
Будем дисконтировать, используя постоянную норму дохода, т.е. предполагая, что инфляция отсутствует или ее значение невелико.
Суммарный дисконтированный поток определим в двух вариантах: при Е = 0,1 и Е = 0,2.
1. Вариант Е = 0,1. Тогда получим:
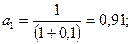
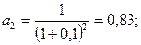

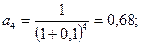

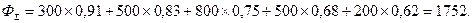
2. Вариант Е = 0,2:
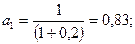
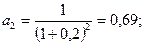
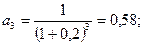
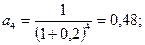


Т.о. с ростом Е величина суммарного дисконтированного потока снижается, и наоборот.
В экономике переходного периода ввиду нестабильных условий развития и связанных с этим колебаний темпа инфляции и других причин Е по периодам развития нестабильна и расчетная формула усложняется.
Формула для определения коэффициента дисконтирования при переменной норме дохода имеет следующий вид:
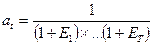 . (14)
. (14)
Пример. Определение суммарного дисконтированного потока при переменной норме дохода (рассмотрим пример, когда норма дохода – величина переменная табл.3).
Таблица 3.
Расчет по формуле (14) дает значения коэффициента дисконтирования (табл.4), а по формуле (12) – дисконтированного потока (табл.5). Определим также суммарный дисконтированный поток при переменной норме дохода для указанных в таблице 2 параметров (см. табл.5).
Расчет коэффициента дисконтирования
Таблица 4
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:

§
Табл. 5
Переменную норму дохода мы в дальнейшем будем использовать для оценки эффективности в прогнозных ценах. Никаких проблем не возникает при ее использовании для расчетов и интерпретации показателя чистого дисконтированного дохода. При оценке другого показателя эффективности ВНД – нужна одна усредненная норма дохода для всего расчетного периода.
4. Чистый дисконтированный доход
Основополагающие принципы оценки экономической эффективности инвестиций соответствуют здравому смыслу экономического поведения человека при принятии решения о целесообразности тех или иных затрат. Они выражены в показателе «чистый доход». При исчислении чистого дохода всегда соизмеряются результаты и затраты.
Если принять, что достигнутые результаты реализации проекта формируются притоками (Р), а затраты и отчисления – оттоками (З), то разность этих двух величин будет составлять экономический эффект, или чистый доход (ЧД). Таким образом:
ЧДm=Рm-Зm, (15)
где m указывает на принадлежность потоков денежных средств к конкретному шагу m расчета.
В развернутом виде формула включает:
Рm=Qm Лm (16)
Зm=Cm Km Д Н, (17)
где Qm – объем продаж;
Лm – поступления от продажи излишних активов;
Cm – операционные издержки (себестоимость за вычетом амортизации);
Km – затраты на приобретение активов;
Д – проценты по кредитам;
Н – налоги.
На первых шагах расчетного периода величина ЧД отрицательна, т.к. выручка от продаж не возмещает всех издержек по проекту. На последующих шагах картина меняется, величина чистого дохода становится положительной и нарастает.
Эффективность проекта следует определять за весь расчетный период, т.е. сложить величины чистого дохода, полученные на всех шагах отчетного периода. Чтобы такое суммирование сделать корректным, т.е. учесть неравноценность денежных средств во времени, годовые показатели чистого дохода следует скорректировать на коэффициент дисконтирования.
| Будущая стоимость чистых доходов, приведенная к их настоящей стоимости, т.е. стоимости через процедуру дисконтирования к начальному шагу расчетного периода, выражает содержание основополагающего показателя – чистого дисконтированного дохода. |
Формула для расчета ЧДД:
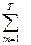 ЧДД =
ЧДД = 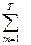 (Рm-Зm)
(Рm-Зm) 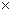
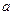 m, (18)
m, (18)
где Рm – результаты, достигаемые на шаге m расчета;
Зm – затраты, осуществляемые на шаге m расчета;
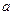 m – коэффициент дисконтирования;
m – коэффициент дисконтирования;
m – номер шага расчета.
Þ Коэффициент дисконтирования определяется требуемым инвестором уровнем нормы дохода (Е) и периодом приведения (t). Отсюда прослеживается следующая зависимость ЧДД от этих параметров:
– с повышением требований инвестора к эффективности проекта ЧДД снижается, и, наоборот, с уменьшением – повышается;
– по мере удаления периода приведения денежного потока от базового размера ЧДД снижается.
Þ Но экономическую эффективность проекта выражает не частное значение ЧДД на конкретном шаге, а размер дохода за весь расчетный период. Поэтому необходимо проводить поступательное суммирование ЧДД всех шагов. Если на m-шаге ЧДД становится положительным и увеличивается за счет прибавления положительных значений ЧДД – то проект следует признать эффективным.
Пример. Оценка приемлемого уровня ЧДД с позиции интересов инвестора.
1. Расчетный период – 6 лет
2. Номер шага обозначается m=0,1,…T, где m=0 – момент стартовых инвестиций (нулевой год)
3. Продолжительность шага расчета равна 1 году
4. Для первого варианта Е=0,1, для второго Е=0,2
5. Исходные данные см. таблицу.
| Показатели | № шага расчетного периода (m) | |||||
| 1. Рm | ||||||
| 2. Зm | ||||||
| 3. Km | ||||||
| 4. Рm– Зm |
! В модифицированном виде формулу (18) можно записать:
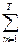 ЧДД =
ЧДД = 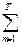 (Рm-Зm*)
(Рm-Зm*) 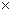
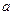 m–
m– 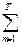 Кm
Кm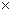
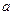 m (19)
m (19)
где Зm* – затраты на шаге m расчета без инвестиционных издержек Кm
Вариант 1. (подставляем данные в формулу (19))
ЧДД=300 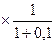 500
500 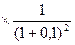 800
800 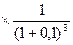 500
500 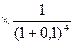
200 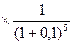 -1500=252>0
-1500=252>0
Вариант 2
ЧДД=300 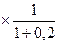 500
500 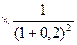 800
800 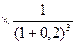 500
500 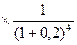
200 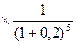 -1500=-122<0
-1500=-122<0
При норме дохода 0,1 величина ЧДД положительна, поэтому вариант инвестирования приемлем.
Вариант 2 не приемлем.
5. Срок окупаемости
Разбиение ЧДД, полученного нарастающим итогом, на два временных периода – до момента превращения отрицательного значения в положительное и после него является основанием определенного срока окупаемости (возмещения) единовременных затрат, измеряемого в месяцах, кварталах, годах.
Срок возмещения определяется периодом от момента начала реализации проекта (начала инвестиционной фазы) до переломного момента в динамике ЧДД определенного нарастающим итогом.
Срок окупаемости может быть получен путем последовательного по шагам расчетного периода вычитания из 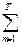 Кm
Кm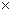
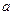 m выражения
m выражения 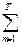 (Рm-Зm*)
(Рm-Зm*) 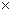
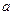 m . Когда эта разность станет равной 0 (полностью возмещена стоимость единовременных затрат) порядковый номер периода – есть срок окупаемости.
m . Когда эта разность станет равной 0 (полностью возмещена стоимость единовременных затрат) порядковый номер периода – есть срок окупаемости.
Þ Для уточнения положения момента окупаемости (когда шаг расчета принят равным году) обычно принимается, что в пределах одного шага поток (S) меняется линейно. Тогда «расстояние» X от начала шага до момента окупаемости, выраженное в продолжительности шага расчета определяется по формуле:
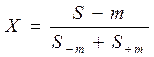 (20)
(20)
где S–m – минусовая величина потока нарастающим итогом на переломном шаге от «-» к « »;
S m – положительная величина потока нарастающим итогом на следующим шаге.
Пример. Определение срока окупаемости инвестиций с учетом момента окупаемости внутри шага расчета.
Величина потока составляет на пятом шаге (S5) 33,3, а на шестом шаге – 13. Из этих данных видно, что срок окупаемости находится внутри шага m-6, т.к. в конце шага m-5 накопленный поток меньше нуля, а аналогичный поток в конце m-6 больше 0. Момент окупаемости внутри искомого шага составит:
 шага
шага
Исходя из этого срок окупаемости, отсчитанный от начала операционной деятельности (конец нулевого периода) составляет 5,72 года, если от начала нулевого шага – 6,72 года.
! Чем меньше срок окупаемости, тем эффективней проект, и это служит сравнительной оценкой с другими проектами.
! Но этот показатель не раскрывает размера чистого дохода за пределами срока окупаемости, в то время как последний может существенно отличаться по разным проектам.
Þ Поэтому этот показатель рассматривается как вспомогательный.
В предыдущем вопросе 4 (ЧДД) в рассмотренном примере при Е=0,1 срок окупаемости от начала реализации проекта больше трех, но меньше четырех лет, а при Е=0,2 расчетный период окупаемости инвестиций вообще не наступает (ЧДД – величина отрицательная).
6. Индексы доходности (ИД)
Базовые потоки денежных средств для расчета ЧД и ЧДД могут быть применены для конструирования еще одной группы вспомогательных показателей – индексов доходности. Такие показатели характеризуют относительную отдачу на вложенные в проект затраты. В зависимости от содержания затрат можно построить индекс дохода инвестиций или индекс дохода всех затрат (текущих и единовременных). Каждый из них, в свою очередь, можно представить в двух видах: по реальным или (и) дисконтированным денежным потокам.
Эти показатели будут иметь различия. Поэтому, характеризуя эффективность ИП посредством ИД, следует подчеркнуть, по какой методике он оценен, а сравнение таких показателей по разным проектам проводить лишь при использовании одних и тех же методик.
Þ Наибольшее распространение на практике получил индекс доходности дисконтированных инвестиций (ИДД). Он представляет собой отношение суммы приведенных эффектов (из которых вычленены инвестиционные затраты) к приведенной к тому же моменту времени величине инвестиционных затрат:
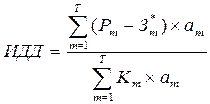 (21)
(21)
ИД строится из тех же элементов, что и ЧДД (см. формулу (19)), и его значение тесно связано с ним: если ЧДД положителен, то и ИД>1 и наоборот, если ИД<1 – проект не эффективен.
В примере вопроса 4 (ЧДД) ИДД (индекс дохода по дисконтированному доходу) по первому варианту – 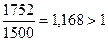 , а по второму варианту –
, а по второму варианту – 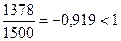 .
.
7. Внутренняя норма дохода
Сложности при расчетах ЧДД связаны с установлением приемлемой нормы дохода. Определение уровня нормы дохода зависит от компетентности специалистов, определяющих экономическую эффективность, и отражает субъективный подход. Влияние данного фактора сведено к минимуму в показателе внутренней нормы дохода – ВНД (или IRR – Internal Rate of Return). Экономическую природу этого показателя можно пояснить с помощью графика зависимости ЧДД от изменений нормы дохода (рис. 1)

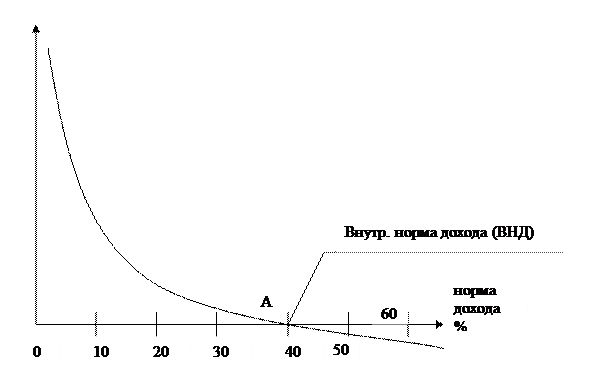
На графике показано, что с ростом требований к эффективности инвестиций (через Е) величина ЧДД уменьшается, достигая нулевого значения при пересечении с осью абсцисс в точке А. Норма дохода, определяющая такое значение ЧДД, является внутренней нормой дохода проекта.
| ВНД характеризует уровень доходности инвестиций, генерируемый конкретным проектом, при условии полного покрытия всех расходов по проекту за счет доходов. |
По своей экономической природе норма дохода (Е) для инвестора и ВНД по проекту идентичны, т.е. характеризует уровень капитализации доходов за расчетный период. Но в первом случае Е (норму дохода) мы привносим извне, обосновывая ее уровень исходя из нашего понимания приемлемого уровня дохода на капитал. Во втором варианте норма дохода формируется на основе объективно складывающихся пропорций результатов и затрат, т.е., исходя из внутренних свойств проекта, степени его прогрессивности. Þ В данном выражении ВНД характеризует гарантированный уровень капитализации доходов, присущий проекту.
Выше было отмечено, что значение показателя ВНД определяется как такое значение нормы дохода Евн, при котором суммы дисконтированных доходов и расходов равны между собой или, что тоже, величина приведенных эффектов (без учета единовременных затрат) равна приведенным единовременным затратам (К). Исходя из данного условия, ВНД (Евн) есть положительный корень уравнения:
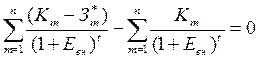 (22)
(22)
Точное значение ВНД определяется по формуле линейной интерполяции:
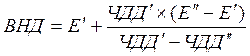 (23)
(23)
где  – норма дисконта, при которой ЧДД принимает ближайшее к 0 положительное (или соответственно отрицательное) значение;
– норма дисконта, при которой ЧДД принимает ближайшее к 0 положительное (или соответственно отрицательное) значение;
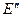 – норма дисконта, повышенная (или пониженная) на 1 пункт по сравнению с
– норма дисконта, повышенная (или пониженная) на 1 пункт по сравнению с  , при которой ЧДД принимает ближайшее к 0 отрицательное (или соответственно положительное) значение;
, при которой ЧДД принимает ближайшее к 0 отрицательное (или соответственно положительное) значение;
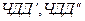 – чистый дисконтированный доход соответственно при
– чистый дисконтированный доход соответственно при  и
и 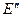 .
.
Значения ЧДД принимаются абсолютными. При этом желательно, чтобы разность значений коэффициентов дисконтирования  и
и 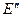 не превышала 0,01 иначе зависимость чистого дисконтированного дохода от величины коэффициента дисконтирования окажется нелинейной. Быстро и точно ВНД определяется с помощью компьютера.
не превышала 0,01 иначе зависимость чистого дисконтированного дохода от величины коэффициента дисконтирования окажется нелинейной. Быстро и точно ВНД определяется с помощью компьютера.
ВНД можно рассчитать графическим методом. На рисунке по оси абсцисс отложены значения Е, по оси ординат – ЧДД, рассчитанный по исходным данным от уровня чистого дохода при избранной величине Е.
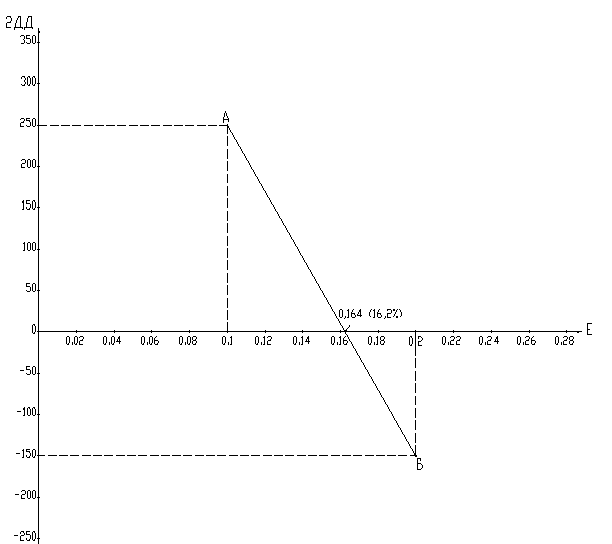
Приведенный график построен по исходным данным примера из вопроса 4 (ЧДД).
Точка А соответствует Е=0,1, а точка Б – Е=0,2. Соединяем точки А и Б, пересечение с осью Е дает искомое значение ВНД. Оно равно 0,162.
Более точный расчет с помощью ПК дает ВНД=0,164 или 16,4%. При этой норме обеспечивается равенство
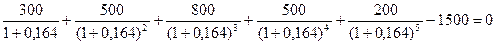
! ВНД объективен и не зависит от требований и условий инвестора, от объема производства и размера инвестиций по проекту. Это делает ВНД выгодным инструментом измерения и управления эффективностью инвестиций, поэтому ВНД непременное требование при оценке экономической эффективности ИП.
 Пример расчета параметров инвестиционного проекта
Пример расчета параметров инвестиционного проекта
Рассмотрим следующий ИП (млн. р.)

Найти: ЧДД; срок окупаемости; индекс доходности PI; внутреннюю норму дохода IRR; ставка дисконтирования равна 20%.
1. Расчет ЧДД
Рассчитаем коэффициент дисконтирования для каждого года и приведем величины элементов денежного потока к базовому году посредством умножения на соответствующие коэффициенты дисконтирования (табл. 1)
| Показатели | ГОДЫ | ЧДД | ||||
| Коэффициенты дисконтирования | (1 0,2)-1= =0,833 | (1 0,2)-2= =0,694 | (1 0,2)-3= =0,579 | (1 0,2)-4= =0,482 | (1 0,2)-5= =0,402 | |
| Дисконтированный денежный поток | -1000   0,833= 0,833==-833 | -500   0,694= 0,694==-347 | 200 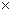 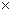 0,579= 0,579==115,8 | 2000 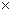 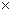 0,482= 0,482==0,64 | 3000 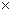 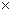 0,402= 0,402==1206 | 1105,8 |
| Наращенный поток | -833 | -1180 | -1064,2 | -100,2 | 1105,8 |
2. Расчет срока окупаемости
Определим дисконтированный срок окупаемости. Сумма дисконтированных инвестиций за два года (1й и 2й) составляет 1180 (833 347). Сумма дохода за два года (3й и 4й) – 1079,8 (115,8 964). Следовательно, инвестиции не окупятся за первые два года получения доходов. За три года сумма дисконтированных доходов составит 2285,8 (115,8 964 1206). Следовательно, на третий год получения доходов (пятый год) инвестиции более чем окупятся.
Величина потока на четвертом шаге составляет -100,2, на пятом шаге 1105,8, т.е. окупаемость наступает внутри пятого года. Определим, за какую часть пятого года окупится оставшаяся часть инвестиций. Воспользуемся формулой (20):
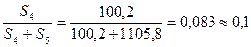 или примерно один месяц.
или примерно один месяц.
Т.о. срок окупаемости с начала периода составит 4 года 1 месяц (с начала операционной деятельности)
3. Индекс доходности
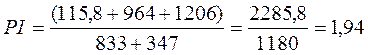
4. Внутренняя норма дохода
Составим уравнение, в котором неизвестной величиной будет норма дохода (доходности) (формула 22):
-1000 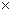 (1 х)-1-500
(1 х)-1-500 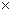 (1 х)-2 200
(1 х)-2 200 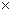 (1 х)-3 2000
(1 х)-3 2000 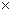 (1 х)-4 3000
(1 х)-4 3000 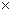 (1 х)-5=0 (Ñ)
(1 х)-5=0 (Ñ)
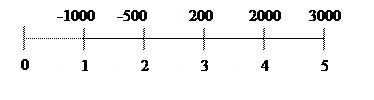
Решим это уравнение методом линейной интерполяции. Для этого зададим верхнюю и нижнюю границы доходности. Возьмем в качестве нижней границы 40%, верхней – 50%. Рассчитаем ЧДДн и ЧДДв (чистый дисконтированный доход для нижнего и верхнего уровней доходности) (смотри пункт 1):
ЧДДн=181,8; ЧДДв=-37,8;
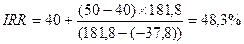 (см. формулу 23)
(см. формулу 23)
При значении нормы доходности равном 48,3% ЧДД составляет -12,77 млн. руб. (см. пункт 1, чтобы рассчитать ЧДД с нормой доходности 48,3). Отсюда видно, что IRR (ВНД) определена не точно. Неточность возникла вследствие наличия большого разрыва между верхней и нижней границами ставки дисконтирования. Поэтому проведем вторую итерацию расчетов. Примем полученную на первой итерации величину IRR (ВНД) за верхнюю границу нормы дохода на втором этапе расчетов. Нижнюю границу возьмем на уровне 45%. Получим:

При таком значении нормы дохода ЧДД=-0,61 млн.р. Можно считать, что такая степень приближения является удовлетворительной. Или можно продолжить расчеты до получения в (Ñ) нулевого значения.
7.1. Внутренняя норма доходности с неординарными денежными потоками
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:

Пример выплаты ипотеки
Для ипотечного кредита в размере 10 000 долларов США сроком на 30 лет и процентной ставкой 4,5%, выплачиваемой ежегодно, мы находим:
- Тзнак равно30{ displaystyle T = 30}
- язнак равно0,045{ displaystyle I = 0,045}
который дает
- Иксзнак равно12яТзнак равно0,675{ displaystyle X = { frac {1} {2}} IT = 0,675}
так что
- п≈п0(1 Икс 13Икс2)знак равно$333,33(1 0,675 0,6752/3)знак равно$608,96{ displaystyle P приблизительно P_ {0} left (1 X { frac {1} {3}} X ^ {2} right) = $ 333,33 (1 0,675 0,675 ^ {2} / 3) = 608,96 долл. США}
Точная сумма платежа является завышенной примерно на одну шестую процента.
пзнак равно$608,02{ displaystyle P = 608,02 долл. США}
Примерная формула ежемесячного платежа
Формулу с точностью до нескольких процентов можно найти, отметив, что для типичных ставок нот США ( и сроков = 10–30 лет) месячная ставка нот мала по сравнению с 1:
так, что дает упрощение, так что
я<8%{ displaystyle I <8 %}Т{ displaystyle T}р<<1{ displaystyle r << 1}пер(1 р)≈р{ Displaystyle пер (1 г) приблизительно г}
- c≈пр1-е-прзнак равнопппр1-е-пр{ displaystyle c приблизительно { frac {Pr} {1-e ^ {- nr}}} = { frac {P} {n}} { frac {nr} {1-e ^ {- nr}} }}
что предлагает определить вспомогательные переменные
- Y≡прзнак равнояТ{ Displaystyle Y Equiv nr = IT}
- c0≡пп{ displaystyle c_ {0} Equiv { frac {P} {n}}}.
Вот ежемесячный платеж, необходимый для выплаты ссуды без процентов в рассрочку. В терминах этих переменных можно записать приближение
c0{ displaystyle c_ {0}}п{ displaystyle n}
- c≈c0Y1-е-Y,{ displaystyle c приблизительно c_ {0} { frac {Y} {1-e ^ {- Y}}},}
Функция четная:
ж(Y)≡Y1-е-Y-Y2{ displaystyle f (Y) Equiv { frac {Y} {1-e ^ {- Y}}} – { frac {Y} {2}}}
- ж(Y)знак равнож(-Y){ Displaystyle f (Y) = f (-Y)}
подразумевая, что он может быть расширен до четных степеней .
Y{ displaystyle Y}Отсюда сразу следует, что можно разложить до четных степеней плюс один член:Y1-е-Y{ displaystyle { frac {Y} {1-e ^ {- Y}}}}Y{ displaystyle Y}Y/2.{ displaystyle Y / 2.}
Тогда будет удобно определить
- Иксзнак равно12Yзнак равно12яТ{ displaystyle X = { frac {1} {2}} Y = { frac {1} {2}} IT}
так что
- c≈c02Икс1-е-2Икс{ displaystyle c приблизительно c_ {0} { frac {2X} {1-e ^ {- 2X}}}}
который можно расширить:
- c≈c0(1 Икс Икс23-145Икс4 …){ displaystyle c приблизительно c_ {0} left (1 X { frac {X ^ {2}} {3}} – { frac {1} {45}} X ^ {4} … Правильно)}
где многоточием обозначены члены более высокого порядка по четной степени . Расширение
Икс{ displaystyle X}
- п≈п0(1 Икс Икс23){ Displaystyle P приблизительно P_ {0} left (1 X { frac {X ^ {2}} {3}} right)}
действительно до более 1% при условии .
Икс≤1{ Displaystyle X leq 1}
Сила интереса
Поскольку количество периодов начисления сложных процентов достигает бесконечности при непрерывном начислении сложных процентов, непрерывная ставка сложных процентов называется силой процента .
п{ displaystyle n}δ{ displaystyle delta}
В математике, функция накопления часто выражается через е , основание натурального логарифма . Это облегчает использование исчисления для управления формулами процентов.
Для любой непрерывно дифференцируемой функции накопления a (t) интересующая сила или, в более общем смысле, логарифмическая или непрерывно вычисляемая доходность является функцией времени, определяемой следующим образом:
- δтзнак равноа′(т)а(т)знак равноddтпера(т){ displaystyle delta _ {t} = { frac {a ‘(t)} {a (t)}} = { frac {d} {dt}} ln a (t)}
Это логарифмическая производная функции накопления.
Наоборот:
- а(т)знак равное∫0тδsds ,{ displaystyle a (t) = e ^ { int _ {0} ^ {t} delta _ {s} , ds} ,}(поскольку ; это можно рассматривать как частный случай интеграла продукта ).а(0)знак равно1{ Displaystyle а (0) = 1}
Когда приведенная выше формула записана в формате дифференциального уравнения, тогда интересующая сила – это просто коэффициент величины изменения:
- dа(т)знак равноδта(т)dт{ Displaystyle да (т) = дельта _ {т} а (т) , дт ,}
Для сложных процентов с постоянной годовой процентной ставкой r сила процента является постоянной, а функция накопления сложных процентов с точки зрения силы процента представляет собой простую степень e :
- δзнак равнопер(1 р){ Displaystyle дельта = пер (1 г) ,} или
- а(т)знак равноетδ{ Displaystyle а (т) = е ^ {т дельта} ,}
Сила процента меньше годовой эффективной процентной ставки, но больше годовой эффективной ставки дисконтирования . Это величина, обратная времени электронного складывания . См. Также обозначение процентных ставок .
Способ моделирования силы инфляции – формула Стодли: где p , r и s оцениваются.
δтзнак равноп s1 рsеsт{ displaystyle delta _ {t} = p {s over {1 rse ^ {st}}}}
Точная формула ежемесячного платежа
Точная формула ежемесячного платежа ( ):
c{ displaystyle c}
- cзнак равнорп1-1(1 р)п{ displaystyle c = { frac {rP} {1 – { frac {1} {(1 r) ^ {n}}}}}}
или эквивалентно
- cзнак равнорп1-е-ппер(1 р){ displaystyle c = { frac {rP} {1-e ^ {- n ln (1 r)}}}}
куда:
- c{ displaystyle c} = ежемесячный платеж
- п{ displaystyle P} = главный
- р{ displaystyle r} = ежемесячная процентная ставка
- п{ displaystyle n} = количество периодов оплаты
Это можно получить, посчитав, сколько еще остается выплачивать по истечении каждого месяца. Принципал, оставшийся после первого месяца, составляет
- п1знак равно(1 р)п-c,{ Displaystyle P_ {1} = (1 r) ПК,}
то есть начальная сумма плюс проценты за вычетом платежа. Если вся ссуда будет погашена через месяц, то
- п1знак равно0{ displaystyle P_ {1} = 0}, так пзнак равноc1 р{ displaystyle P = { frac {c} {1 r}}}
По прошествии второго месяца так
п2знак равно(1 р)п1-c{ Displaystyle P_ {2} = (1 r) P_ {1} -c}
- п2знак равно(1 р)((1 р)п-c)-c{ Displaystyle P_ {2} = (1 r) ((1 r) Pc) -c}
Если вся ссуда была погашена через два месяца,
- п2знак равно0{ displaystyle P_ {2} = 0}, так пзнак равноc1 р c(1 р)2{ displaystyle P = { frac {c} {1 r}} { frac {c} {(1 r) ^ {2}}}}
Это уравнение обобщает на срок п месяцев . Это геометрический ряд с суммой
пзнак равноc∑jзнак равно1п1(1 р)j{ displaystyle P = c sum _ {j = 1} ^ {n} { frac {1} {(1 r) ^ {j}}}}
- пзнак равноcр(1-1(1 р)п){ displaystyle P = { frac {c} {r}} left (1 – { frac {1} {(1 r) ^ {n}}} right)}
который можно переставить, чтобы получить
- cзнак равнопр1-1(1 р)пзнак равнопр1-е-ппер(1 р){ displaystyle c = { frac {Pr} {1 – { frac {1} {(1 r) ^ {n}}}}} = { frac {Pr} {1-e ^ {- n ln (1 r)}}}}
- Формула электронной таблицы
В электронных таблицах используется функция PMT () . Синтаксис:
- PMT (процентная ставка, количество_платежей, настоящее_значение, будущее_значение, [Тип])
См. Excel , Номера Mac , LibreOffice , Open Office , Google Таблицы для получения более подробной информации.
Например, для процентной ставки 6% (0,06 / 12), 25 лет * 12 в год, PV 150 000 долларов США, FV 0, тип 0 дает:
- = PMT (0,06 / 12, 25 * 12, -150000, 0, 0)
- = 966,45 долл. США
![r_2 = left [ left (1 frac {r_1} {n_1} right) ^ frac {n_1} {n_2} -1 right] {n_2},](https://wikimedia.org/api/rest_v1/media/math/render/svg/58a91c24fd5ef43e7b584e4f740ff3dee69bdfdc)






































































