Инвестиции. решение задач – презентация, доклад, проект
3. Выбор эффективного инвестиционного проекта
Задача 11. Решение:
Проранжируем проекты по критериальным показателям т.о., что
проект, имеющий наилучшее значение, по данному показателю получит наивысший ранг (в нашем примере «4»),
а проект, имеющий наихудшее значение – низший ранг – «1».
И найдем сумму рангов.
Контрольная – решенные задачи по инвестициям
20 страниц. Интеллектуальные инвестиции Проектирование инвестиций Задача Список использованной литературы На предприятии оценивают два инвестиционных проекта. Эти проекты являются взаимоисключающими, поскольку предполагается использование одних и тоже производственных площадей, хотя ограничения на инвестиции отсутствуют. Год Проект ВВ, тис. грн. Проект ОВ, тис. грн. 0 350,0 550,0 1-й год 150,0 250,0 2-й год 150,0 250,0 3-й год 150,0 250,0 Диско…
Решение задач по инвестиционному анализу 2
Ниже приведены условия и решения задач. Закачка решений в формате doc и mcd начнется автоматически через 10 секунд.
Задача №1
Предприятие собирается приобрести оборудование, чтобы самостоятельно производить детали, которые раньше покупали от поставщиков. Стоимость оборудования — 500000. Эксплуатационные расходы в первый год составляют100000 и ежегодно возрастают на 10000. За поставку деталей ежегодно платили поставщикам по 250000. Срок эксплуатации оборудования – 5 лет. Ликвидационная стоимость – 30000 (чистый доход от продажи оборудования в конце 5-го года). Ставка по альтернативным проектам- 8% годовых. Эффективна ли данная инвестиция (NPV, PI, IRR, MIRR, PP, PPD)? Дайте письменное заключение о целесообразности реализации проекта.
Решение.
Период | Отток средств | Приток средств | Поток платежей | Коэффициент дисконтирования | Дисконтированный поток платежей | ||
(t) | Kt | Dt | (CFt) |
| DCFt | Kt·t | Dt·t |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
0 | -500000 | 0 | -500000 | 1 | -500000 | -500000 | 0 |
1 | -100000 | 250000 | 150000 | 0,92593 | 138888,889 | -92593 | 231481 |
2 | -110000 | 250000 | 140000 | 0,85734 | 120027,435 | -94307 | 214335 |
3 | -120000 | 250000 | 130000 | 0,79383 | 103198,191 | -95260 | 198458 |
4 | -130000 | 250000 | 120000 | 0,73503 | 88203,5823 | -95554 | 183757 |
5 | -140000 | 280000 | 140000 | 0,68058 | 95281,6476 | -95282 | 190563 |
Итого | – | – | – | – | 45599,745 | -972995 | 1018595 |
Для проекта определяем приведенную стоимость поступлений от инвестиций по формуле:
![]()
, где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
NPV = 31443,6
Определим индекс прибыльности.
ИД определим по формуле:
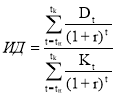
Индекс прибыльности:
PI = 1018595/972995 = 1,047
Внутренняя норма доходности (IRR) – это такая норма дисконта, при которой сумма дисконтированных доходов за жизненный цикл проекта равна сумме дисконтированных инвестиций.
Определим внутреннюю норму доходности для каждого из проектов.
Для первого проекта решим уравнение:
∑ CFk / ( 1 IRR )k = ∑ INVt / (1 IRR) t
![]()
Решим уравнение аналитически, методом подбора.
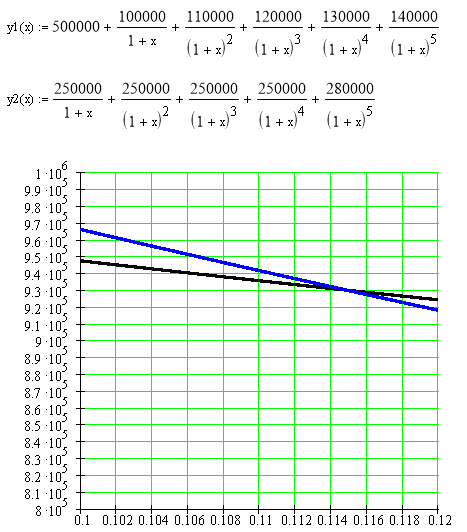
Следовательно, IRR = 0,115.
Определим срок окупаемости для проектас учетом дисконтирования.
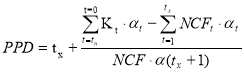
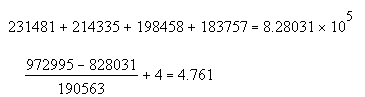
PPD = 4,761.
При ставке сравнения 8% имеет смысл инвестировать средства в данный проект, имеем положительный чистый дисконтированный доход, индекс доходности 104,7%. Однако при увеличении инфляции свыше 11,5% не имеет смысла инвестировать средства в данный проект (IRR=0,115), так же срок окупаемости проекта достаточно высокий и составляет 4,761 года, и близок к эксплуатационному сроку работы оборудования.
Задача №2
Фирма «Смирнов и Андрианов» покупает завод по производству глиняной посуды за 100 млн.рублей. Кроме того расчёты показывают, что для модернизации этого предприятия в первый же год потребуются дополнительные затраты в 50 млн. рублей. Однако, при этом предполагается, что в последующие 9 лет этот завод будет обеспечивать ежегодные денежные поступления по 25 млн. рублей. Затем, через 10 лет, предполагается, что фирма продаст завод по остаточной стоимости, которая составит согласно расчётам 80 млн. рублей. Средняя ставка доходности 10%. Эффективна ли данная инвестиция (NPV, PI, IRR, MIRR, PP, PPD)? Дайте письменное заключение о целесообразности реализации проекта
Решение.
Период | Отток средств | Приток средств | Поток платежей | Коэффициент дисконтирования | Дисконтированный поток платежей | ||
(t) | Kt | Dt | (CFt) |
| DCFt | Kt·t | Dt·t |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
0 | -100 | 0 | -100 | 1 | -100 | -100 | 0 |
1 | -50 | 25 | -25 | 0,90909091 | -22,7272727 | -45,455 | 22,7273 |
2 | 25 | 25 | 0,82644628 | 20,661157 | 0 | 20,6612 | |
3 | 25 | 25 | 0,7513148 | 18,78287 | 0 | 18,7829 | |
4 | 25 | 25 | 0,68301346 | 17,0753364 | 0 | 17,0753 | |
5 | 25 | 25 | 0,62092132 | 15,5230331 | 0 | 15,523 | |
6 | 25 | 25 | 0,56447393 | 14,1118483 | 0 | 14,1118 | |
7 | 25 | 25 | 0,51315812 | 12,828953 | 0 | 12,829 | |
8 | 25 | 25 | 0,46650738 | 11,6626845 | 0 | 11,6627 | |
9 | 105 | 105 | 0,42409762 | 44,5302499 | 0 | 44,5302 | |
Итого | – | – | – | – | 32,4488594 | -145,45 | 177,903 |
Для проекта определяем приведенную стоимость поступлений от инвестиций по формуле:
![]()
, где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
NPV = 3245
Определим индекс прибыльности.
ИД определим по формуле:
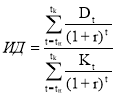
Индекс прибыльности:
PI = 177,9/145,45 = 1,223
Внутренняя норма доходности (IRR) – это такая норма дисконта, при которой сумма дисконтированных доходов за жизненный цикл проекта равна сумме дисконтированных инвестиций.
Определим внутреннюю норму доходности для каждого из проектов.
Для первого проекта решим уравнение:
∑ CFk / ( 1 IRR )k = ∑ INVt / (1 IRR) t
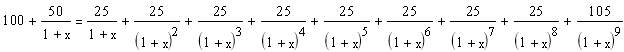
Решим уравнение аналитически, методом подбора.
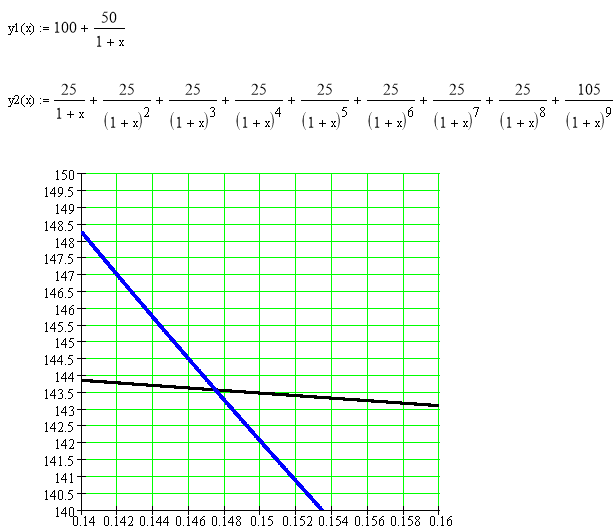
Следовательно, IRR = 0,147.
Определим срок окупаемости для проектас учетом дисконтирования.
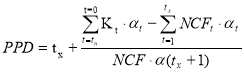
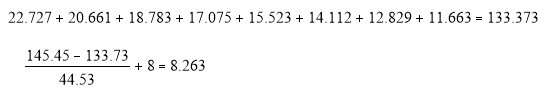
PPD = 8,263.
При ставке сравнения 10% имеет смысл инвестировать средства в данный проект, имеем положительный чистый дисконтированный доход, индекс доходности 122,3%. Однако при увеличении инфляции свыше 14,7% не имеет смысла инвестировать средства в данный проект (IRR=0,147), так же срок окупаемости проекта достаточно высокий и составляет 8,263 года, и близок к эксплуатационному сроку работы оборудования.
Задача №3
Городской мясокомбинат планирует приобрести ещё один холодильник, для чего сначала необходимо подготовить помещение. Эти подготовительные работы займут год и составят в денежном выражении 5 млн.р. Сама же холодильная камера будет куплена в конце этого года за 30 млн.р. и будет эксплуатироваться 3 года. Денежные поступления соответственно составят 10, 15 и 20 млн.р. Требуемый уровень доходности – 10%.
Эффективна ли данная инвестиция (NPV, PI, IRR, MIRR, PP, PPD)? Дайте письменное заключение о целесообразности реализации проекта
Решение.
Период | Отток средств | Приток средств | Поток платежей | Коэффициент дисконтирования | Дисконтированный поток платежей | ||
(t) | Kt | Dt | (CFt) |
| DCFt | Kt·t | Dt·t |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
0 | -5 | 0 | -5 | 1 | -5 | -5 | 0 |
1 | -30 | 10 | -20 | 0,90909091 | -18,1818182 | -27,27 | 9,09091 |
2 | 0 | 15 | 15 | 0,82644628 | 12,3966942 | 0 | 12,3967 |
3 | 0 | 20 | 20 | 0,7513148 | 15,026296 | 0 | 15,0263 |
Итого | – | – | – | – | 4,24117205 | -32,27 | 36,5139 |
Для проекта определяем приведенную стоимость поступлений от инвестиций по формуле:
![]()
, где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
NPV =4,24
Определим индекс прибыльности.
ИД определим по формуле:
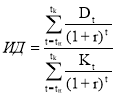
Индекс прибыльности:
PI = 36,51/32,27 = 1,131
Внутренняя норма доходности (IRR) – это такая норма дисконта, при которой сумма дисконтированных доходов за жизненный цикл проекта равна сумме дисконтированных инвестиций.
Определим внутреннюю норму доходности для каждого из проектов.
Для первого проекта решим уравнение:
∑ CFk / ( 1 IRR )k = ∑ INVt / (1 IRR) t
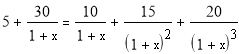
Решим уравнение аналитически, методом подбора.
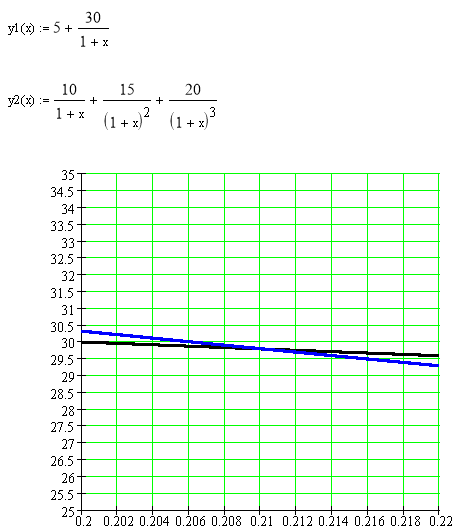
Следовательно, IRR = 0,21.
Определим срок окупаемости для проектас учетом дисконтирования.
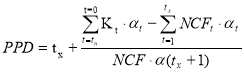
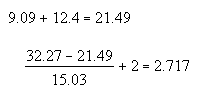
PPD = 2,717.
При ставке сравнения 10% имеет смысл инвестировать средства в данный проект, имеем положительный чистый дисконтированный доход, индекс доходности 131,1%. Однако при увеличении инфляции свыше 21% не имеет смысла инвестировать средства в данный проект (IRR=0,21).Cрок окупаемости проекта составляет 2,717 года.
Список использованной литературы
- Жуленев С.В. Финансовая математика. – М.: изд-во МГУ, 2002. – 628 c.
- Ковалев В.В. Финансовый анализ: управление капиталом. Выбор инвестиций. Анализ отчетности. 2-е изд. – М.: Финансы и статистика, 2004. – 709 с.
- Павлова Л.П. Финансовый менеджмент: Учебник. – М.: Норма, ИНФРА-М.: 2003. – 633 с.
- Теплова Т.В. Финансовый менеджмент: управление капиталом и инвестициями: Учебник. – М.: ГУВШЭ, 2005. – 582 с.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.





