- Расчет основных макроэкономических показателей: Задача
- Сборник задач с ответами и описанием решений по разделу «макроэкономика»
- Расчет отдельных элементов ввп Задача
- Расчет ввп по доходам (распределительным методом): Задача
- Английская, немецкая и французская практики начисления процентов
- Задача 1.
- Задача 10.
- Задача 11.
- Задача 12.
- Задача 13.
- Задача 14.
- Задача 15.
- Задача 16.
- Задача 17.
- Задача 18.
- Задача 19.
- Задача 20.
- Задача 21.
- Задача 22.
- Задача 23.
- Задача 24.
- Задача 25.
- Задача 26.
- Задача 27.
- Задача 28.
- Задача 29.
- Задача 3.
- Задача 30.
- Задача 31.
- Задача 32.
- Задача 33.
- Задача 34.
- Задача 35.
- Задача 36.
- Задача 37.
- Задача 4.
- Задача 5.
- Задача 6.
- Задача 7.
- Задача 8.
- Задача 9.
- Задача: решение задач по макроэкономике
- Контрольная – решенные задачи по инвестициям
- Математическое дисконтирование
- Нахождение эквивалентной номинальной сложной процентной ставки для сложной процентной ставки
- Нахождение эквивалентной простой процентной ставки для номинальной сложной процентной ставки
- Нахождение эквивалентной простой процентной ставки для сложной процентной ставки
- Нахождение эквивалентной сложной процентной ставки для номинальной сложной процентной ставки.
- Начисление сложных процентов несколько раз в году. номинальная процентная ставка
- Непрерывное начисление сложных процентов
- Ответы на вопросы по заказу заданий по инвестициям:
- Проанализируйте предложенную таблицу (данные гипотетические).
- Решение задач по инвестиционному анализу 2
- Решение:
- Сложные ставки ссудных процентов
- Случай изменения простой ставки ссудного процента
- Случай изменения сложной ставки ссудного процента
- Случай, когда период начисления не является целым числом
- Тема 1. макроэкономические показатели
Расчет основных макроэкономических показателей: Задача
Предлагаются следующие данные по
экономике страны.
Показатели (млрд. ден. ед.)
сумма
Трансфертные платежи | 4,0 |
Валовые внутренние инвестиции | 16,2 |
Косвенные налоги | 7,0 |
Подоходный налог | 2,6 |
Чистый экспорт | 1,1 |
Нераспределенная прибыль корпораций | 2,8 |
Амортизация | 7,9 |
Личные потребительские расходы | 77,2 |
Налоги на прибыль корпораций | 1,4 |
Взносы на социальное страхование | 0,2 |
Государственные закупки товаров и | 8,5 |
Задание:
Рассчитайте показатель ВНП.
Найдите чистый национальный продукт
(ЧНП).Рассчитайте величину национального
доходаЧему равен личный доход и располагаемый
личный доход?
Сборник задач с ответами и описанием решений по разделу «макроэкономика»
Государственный стандарт
экономического образования предусматривает усвоение студентами высших учебных
заведений России не только теоретического, но практического материала по курсу
«Экономическая теория».
Настоящее издание представляет собой сборник задач с ответами и описанием
решений, а также рекомендуемой литературы по разделу «Макроэкономика». Материал
задачника расположен в соответствии с темами программы изучаемого курса.
Предлагаемые в данном издании задачи, отражают опыт преподавания курса
экономической теории на кафедре экономики и маркетинга МГТУ им. Г. И. Носова и
ориентированы в первую очередь на студентов заочной формы обучения, позволит им
самим выяснить, насколько глубоко они усвоили предмет.
Тема 1. МАКРОЭКОНОМИЧЕСКИЕ
ПОКАЗАТЕЛИ
Задача
1. По данным
таблицы рассчитайте: а) объём ВНП по потоку расходов;
б) объём ВНП по потоку доходов;
в) объём ЧНП;
г) объём НД.
Счёт | Млрд. ден. ед. |
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. | 10 20 105 150 1000 340 400 25 610 3000 410 500 3300 |
Решение:
а) Исходя из основного
макроэкономического тождества: ВНП (Y)
= С I G
Xn, где С —
потребительские расходы,
G — государственные закупки товаров и
услуг,
I — инвестиции валовые,
Xn — чистый
экспорт.
Складываем
показатели потребительских расходов (3 300), валовых инвестиций (610),
государственных закупок (1 000) и чистого экспорта (20). Получим ВНП по
расходам = 4 930 млрд. ден. ед. б) ВНП по доходам определяем путем
сложения нераспределенной прибыли корпораций (10), дивидендов (105), налогов
на прибыль корпораций (10), доходов от индивидуальных вложений (340)
, процентов
(400), арендной платы (25), заработной платы наемных работников (3 000)
косвенных налогов на бизнес (400), объёма потребленного капитала (амортизации)
(500). Получаем ВНП по доходам = 4 930 млрд. ден. ед. ВНП по расходам равен ВНП
по доходам. в) ЧНП = ВНП – амортизация;
ЧНП
= 4 930 – 500 = 4 430 млрд. ден. ед.;
г) НД = ЧНП – косвенные налоги на бизнес;
НД
= 4 430 – 400 = 4 030 млрд. ден. ед.
Задача 2.
Имеются
следующие данные по экономике гипотетической страны за год ( млрд. ден. ед)
Счета млрд. ден. ед.
_________________________________________________________
Трансфертные
платежи 4
Валовые внутренние
инвестиции 16
Косвенные налоги на
бизнес 7
Личные подоходные
налоги 2, 5
Чистый
экспорт 1, 5
Нераспределенные
прибыли корпораций 3
Амортизация 8
Личные
потребительские расходы 78
Налоги на прибыль
корпораций 2
Взносы на
социальное страхование 0, 5
Государственные
закупки товаров и услуг 8, 5
Рассчитайте: а)
показатель ВНП, б) личного располагаемого дохода, в) величину частных сбережений (Sp).
Решение: а) Исходя из
данных приведенных в условии задачи, можно рассчитать ВНП по расходам (для
расчета по доходам не хватает информации).
ВНП (Y) = С I G Xn; ВНП = 78 16 8,5
1,5 = 104
б) Чтобы рассчитать
величину личного располагаемого дохода, мы должны найти вначале чистый
национальный продукт (ЧНП), национальный доход (НД) и личный доход (ЛД):
ЧНП = ВНП —
амортизация; ЧНП = 104 – 8 = 96
НД = ЧНП –
косвенные налоги на бизнес
НД = 96 – 7 = 89
ЛД = НД – взносы на
социальное страхование — нераспределенная прибыль корпораций — налоги на
прибыль корпораций трансфертные платежи.
ЛД = 89 – 05 –3 – 2
4 = 87, 5
Располагаемый
личный доход (РЛД) равен личному доходу за вычетом подоходных налогов:
РЛД = 87, 5 – 2, 5
= 85
в) Располагаемые
личные доходы используются на потребление, а часть превращается в сбережения (Sp). Следовательно, частные сбережения
могут быть получены путем вычитания личных потребительских расходов из
располагаемого личного дохода: Sp = РЛД – С = 85 — 78 = 7.
Расчет отдельных элементов ввп Задача
Предложены следующие условия:
ВНП = 10000 д. ед.
Потребительские расходы составили
7800 ден. ед.
Государственные расходы равны 450 ден.
ед..
Чистый экспорт равнялся 150 ден.ед..
Рассчитайте:
Величину инвестиций.
Объем импорта, при условии, что объем
экспорта составляет 350 д.ед.ЧНП, при условии, что амортизационные
отчисления равны 480 ден. ед.
Расчет ввп по доходам (распределительным методом): Задача
Страна А имеет такие макроэкономические
показатели (млрд. евро). Рассчитайте ВВП
по доходам.
зарплата- 156;
доход от индивидуального бизнеса — 48;
амортизация — 26;
валовая корпоративная прибыль — 96;
непрямые налоги-37;
субсидии-12.
Решение:
При
расчете ВВП по доходам суммируются все
виды доходов, а также два компонента,
не являющиеся доходами в чистом виде
(амортизация и косвенные налоги на
бизнес). Косвенные налоги рассчитываются
как разница между непрямыми налогами
и субсидиями бизнесу. Поэтому:
ВВП= 156 48 26 96 (37-12)=351 млрд.евро.
Английская, немецкая и французская практики начисления процентов
В формуле  период начисления
период начисления  измеряется в годах. Это не всегда удобно, так как период начисления может быть меньше года (например, с 18 марта 2004 года по 20 октября 2004 года). В этом случае полагают
измеряется в годах. Это не всегда удобно, так как период начисления может быть меньше года (например, с 18 марта 2004 года по 20 октября 2004 года). В этом случае полагают  где
где  — период начисления (в днях),
— период начисления (в днях),  — продолжительность года (в днях). Тогда
— продолжительность года (в днях). Тогда  Дата выдачи и дата погашения ссуды всегда считаются за один день.В немецкой практике начисления процентов один полный месяц равен 30 дням, продолжительность года
Дата выдачи и дата погашения ссуды всегда считаются за один день.В немецкой практике начисления процентов один полный месяц равен 30 дням, продолжительность года  дней. Во французской практике период начисления процентов равен фактическому сроку, продолжительность года
дней. Во французской практике период начисления процентов равен фактическому сроку, продолжительность года  дней. В английской практике период начисления процентов равен фактическому сроку, продолжительность года
дней. В английской практике период начисления процентов равен фактическому сроку, продолжительность года  дней (невисокосный год) или 366 дней (високосный год).
дней (невисокосный год) или 366 дней (високосный год).
Задача 1.
На основе
данных о размере годового дохода на одного члена семьи и размере потребления
рассчитайте сбережения по каждой группе семей, а также предельную склонность к
потреблению (МРС) и предельную склонность к сбережению (МРS). Расчеты можно оформить в таблице.
Группа семей | Доход на одного члена семьи | Расходы на потребление | Предельная склонность к потреблению МРС | Сбережения S | Предельная склонность к сбережению |
А | 900 | 900 | |||
Б | 1200 | 1140 | |||
В | 1800 | 1608 | |||
Г | 2400 | 2052 |
Для заполнения таблицы нам понадобятся
следующие формулы:
Доход = Потребление Сбережения = Y
= C S, где Y – доход, С- потребление; S – сбережения. Отсюда находим, что S = Y – С. Рассчитаем S:
900 – 900 = 0; 1200 – 1140 = 60; 1800 – 1608 = 192; и т. д. Результат занесем в
таблицу.
Для
расчета предельной склонности к потреблению и предельной
Задача 10.
Первоначальная сумма  В первой половине года применялась простая процентная ставка
В первой половине года применялась простая процентная ставка  годовых, во второй половине года применялась простая процентная ставка
годовых, во второй половине года применялась простая процентная ставка  годовых.Тогда наращенная сумма
годовых.Тогда наращенная сумма 

Задача 11.
Первоначальная сумма  В первой половине года применялась простая процентная ставка
В первой половине года применялась простая процентная ставка  годовых, во второй половине года применялась простая процентная ставка
годовых, во второй половине года применялась простая процентная ставка  годовых. Найти наращенную сумму.
годовых. Найти наращенную сумму.
Задача 12.
Первоначальная сумма  руб. помещена в банк на
руб. помещена в банк на  года под
года под  годовых (проценты сложные).Тогда наращенная сумма после двух лет
годовых (проценты сложные).Тогда наращенная сумма после двух лет 

Задача 13.
Первоначальная сумма  помещена в банк на
помещена в банк на  года под
года под  годовых (проценты сложные). Найти наращенную сумму.Зная первоначальную сумму
годовых (проценты сложные). Найти наращенную сумму.Зная первоначальную сумму  наращенную сумму
наращенную сумму  сложную годовую процентную ставку
сложную годовую процентную ставку  можно определить период начисления
можно определить период начисления  (в годах):
(в годах):
Задача 14.
Первоначальная сумма  руб., наращенная сумма
руб., наращенная сумма  годовых (проценты сложные).Тогда период начисления
годовых (проценты сложные).Тогда период начисления 
 года.
года.
Задача 15.
Первоначальная сумма  руб., наращенная сумма
руб., наращенная сумма  годовых (проценты сложные). Найти период начисления.Зная первоначальную сумму
годовых (проценты сложные). Найти период начисления.Зная первоначальную сумму  наращенную сумму
наращенную сумму  период начисления
период начисления  (в годах), можно определить сложную годовую процентную ставку
(в годах), можно определить сложную годовую процентную ставку 
Задача 16.
Первоначальная сумма  руб., наращенная сумма
руб., наращенная сумма  руб., период начисления
руб., период начисления  года. Тогда сложная процентная ставка
года. Тогда сложная процентная ставка 

Задача 17.
Первоначальная сумма  руб., наращенная сумма
руб., наращенная сумма  руб., период начисления
руб., период начисления  года. Найти сложную процентную ставку.
года. Найти сложную процентную ставку.
Задача 18.
Наращенная сумма  руб., период начисления
руб., период начисления  года, сложная процентная ставка
года, сложная процентная ставка  годовых. Тогда первоначальная сумма
годовых. Тогда первоначальная сумма 

Задача 19.
Наращенная сумма  руб., период начисления
руб., период начисления  года, сложная процентная ставка
года, сложная процентная ставка  годовых.
годовых.
Найти первоначальную сумму.
Задача 20.
Чему равны целые части чисел -3,5 и 2,9?
Определение. Дробная часть  числа
числа  — это разность между числом
— это разность между числом  и его целой частью:
и его целой частью:  Всегда
Всегда 
Задача 21.
Чему равны дробные части чисел -4,5 и 1,9?
Если период начисления  не является целым числом, то
не является целым числом, то  (целая часть)
(целая часть)  (дробная часть). Тогда наращенная сумма
(дробная часть). Тогда наращенная сумма 
Задача 22.
Первоначальная сумма  руб. помещена в банк на
руб. помещена в банк на  года под
года под  годовых (проценты сложные).
годовых (проценты сложные).
Найдем наращенную сумму двумя способами.
Задача 23.
Первоначальная сумма  руб. помещена в банк на
руб. помещена в банк на  года под
года под  годовых (проценты сложные). Найти наращенную сумму двумя способами.
годовых (проценты сложные). Найти наращенную сумму двумя способами.
Задача 24.
Первоначальная сумма  года применялась сложная процентная ставка
года применялась сложная процентная ставка  годовых, затем
годовых, затем  года применялась сложная процентная ставка
года применялась сложная процентная ставка  годовых.Тогда наращенная сумма
годовых.Тогда наращенная сумма 

Задача 25.
Первоначальная сумма  руб.,
руб.,  года применялась сложная процентная ставка
года применялась сложная процентная ставка  годовых, затем
годовых, затем  года применялась сложная процентная ставка
года применялась сложная процентная ставка  годовых. Найти наращенную сумму.
годовых. Найти наращенную сумму.
Задача 26.
Первоначальная сумма  руб., период начисления
руб., период начисления  года, сложная процентная ставка
года, сложная процентная ставка  годовых ежеквартально. Найдем наращенную сумму.
годовых ежеквартально. Найдем наращенную сумму. (в году 4 квартала). Тогда наращенная сумма
(в году 4 квартала). Тогда наращенная сумма 

Задача 27.
Первоначальная сумма  руб., период начисления
руб., период начисления  года, сложная процентная ставка
года, сложная процентная ставка  годовых ежемесячно. Найти наращенную сумму.
годовых ежемесячно. Найти наращенную сумму.
Задача 28.
Первоначальная сумма  руб., период начисления
руб., период начисления  года, сложная процентная ставка
года, сложная процентная ставка  годовых. Начисление процентов происходит непрерывно. Найдем наращенную сумму.
годовых. Начисление процентов происходит непрерывно. Найдем наращенную сумму.
Задача 29.
Найти наращенную сумму в задаче 15 при непрерывном начислении процентов. Сравнить с результатом задачи 15.
Сравнение операций
В предыдущих главах мы изучили простые и сложные процентные ставки. Очень часто перед инвестором стоит задача выбора одного из этих вариантов инвестирования первоначальной суммы. Как выбрать вариант, при котором наращенная сумма будет максимальна? Возникает задача сравнения между собой различных процентных ставок.
Две ставки называются эквивалентными, если при одинаковой первоначальной сумме  и на одинаковом периоде начисления
и на одинаковом периоде начисления  они приводят к одинаковой наращенной сумме
они приводят к одинаковой наращенной сумме  При сравнении двух ставок из разных классов для одной из них находят эквивалентную ей ставку из другого класса и проводят сравнение двух ставок из одного класса.
При сравнении двух ставок из разных классов для одной из них находят эквивалентную ей ставку из другого класса и проводят сравнение двух ставок из одного класса.
Задача 3.
ВНП равен 6000 ден. ед. Потребительские расходы равны 4200 ден. ед.,
государственные расходы равны 900 ден.ед., а чистый экспорт равен 120 ден. ед.
Рассчитайте: а)
величину валовых и чистых инвестиций;
б)
объём импорта при условии, что экспорт равен 450 ден. ед.;
в)
ЧНП при условии, что амортизация равна 200 ден. ед.
Решение:
а)
Исходя из основного макроэкономического тождества
ВНП
= С I G
Xn, где С — потребительские
расходы, G — государственные закупки товаров и
услуг, I — валовые инвестиции, Xn — чистый
экспорт, находим валовые инвестиции:
I
= ВНП — С — G
— Xn = 6000 — 4200 — 900 — 120 = 780 ден. ед.
Чистые
инвестиции = валовые инвестиции – амортизация = 780 ден. ед. – 200 ден. ед. =
580 ден. ед.
б)
Импорт = Экспорт – Чистый экспорт = 450 – 120 = 330 ден. ед.
в)
ЧНП = ВНП – амортизация = 6000 – 200 = 5800 ден. ед.
Задача 4.
Определите валовый национальный
продукт и сумму повторного счета по следующим исходным данным.
Стадии | Стоимость |
«Фирма | 200 |
«Фирма | 250 |
«Фирма | 400 |
«Фирма | 500 |
«Фирма | 800 |
«Фирма | 900 |
«Фирма | 1000 |
Общая | 4050 |
Решение:
На основе данных
таблицы ВНП можно определить производственным методом, суммируя стоимость,
добавленную на каждой стадии производства конечного продукта.
Стоимость
промежуточных продуктов не учитывается.
ВНП = 200 (250 –200)
(400 – 250) (500 –400) (800 –500) (900—800) (1000 – 900) = 1000 ден.
ед.
Таким образом, величина добавленной
стоимости равна стоимости конечной продукции, что отражается в розничной
цене продукции. Размер повторного счета определяется как разница между общей
стоимостью продаж и добавленной стоимостью, 4 050 – 1 000 = 3 050 ден. ед.
Задача 30.
Какой вариант инвестирования первоначальной суммы на  года лучше: под простую процентную ставку 18% годовых или под сложную процентную ставку 15% годовых?Найдем эквивалентную простую процентную ставку для сложной процентной ставки
года лучше: под простую процентную ставку 18% годовых или под сложную процентную ставку 15% годовых?Найдем эквивалентную простую процентную ставку для сложной процентной ставки  годовых на периоде начисления
годовых на периоде начисления  года.
года.
 Лучше вариант с простой процентной ставкой.
Лучше вариант с простой процентной ставкой.
Задача 31.
Какой вариант инвестирования первоначальной суммы на  года лучше: под простую процентную ставку 17% годовых или под сложную процентную ставку 15,5% годовых?Замечание. Выразив из равенства
года лучше: под простую процентную ставку 17% годовых или под сложную процентную ставку 15,5% годовых?Замечание. Выразив из равенства  ставку
ставку  через
через  мы найдем эквивалентную сложную процентную ставку
мы найдем эквивалентную сложную процентную ставку  для простой процентной ставки
для простой процентной ставки 
Задача 32.
Какой вариант инвестирования первоначальной суммы на  года лучше: под простую процентную ставку 18% годовых или под сложную процентную ставку 15% годовых ежеквартально?Найдем эквивалентную простую процентную ставку для номинальной сложной процентной ставки
года лучше: под простую процентную ставку 18% годовых или под сложную процентную ставку 15% годовых ежеквартально?Найдем эквивалентную простую процентную ставку для номинальной сложной процентной ставки  годовых (здесь
годовых (здесь  на периоде начисления
на периоде начисления  года.
года.
 Лучше вариант с номинальной сложной процентной ставкой.
Лучше вариант с номинальной сложной процентной ставкой.
Задача 33.
Какой вариант инвестирования первоначальной суммы на  года лучше: под простую процентную ставку 19% годовых или под сложную процентную ставку 14% годовых ежемесячно?Замечание. Выразив из равенства
года лучше: под простую процентную ставку 19% годовых или под сложную процентную ставку 14% годовых ежемесячно?Замечание. Выразив из равенства  ставку
ставку  через
через  мы найдем эквивалентную номинальную сложную процентную ставку
мы найдем эквивалентную номинальную сложную процентную ставку  для простой процентной ставки
для простой процентной ставки 
Задача 34.
Найдем эффективную годовую ставку сложных процентов, эквивалентную номинальной сложной процентной ставке  годовых ежеквартально.Здесь
годовых ежеквартально.Здесь  Тогда
Тогда 
 Вместо начисления каждый квартал 2,5% можно один раз в год начислять 10,4%. От этого наращенная сумма не изменится.
Вместо начисления каждый квартал 2,5% можно один раз в год начислять 10,4%. От этого наращенная сумма не изменится.
Задача 35.
Найти эффективную годовую ставку сложных процентов, эквивалентную номинальной сложной процентной ставке  годовых ежемесячно.Замечание. Мастер функций
годовых ежемесячно.Замечание. Мастер функций  пакета Excel содержит финансовые функции
пакета Excel содержит финансовые функции  финансовые). Их количество значительно возрастет после установки надстройки Пакет анализа (Сервис – Надстройки – Пакет анализа). В частности, финансовая функция ЭФФЕКТ (EFFECT) возвращает эффективную годовую ставку сложных процентов
финансовые). Их количество значительно возрастет после установки надстройки Пакет анализа (Сервис – Надстройки – Пакет анализа). В частности, финансовая функция ЭФФЕКТ (EFFECT) возвращает эффективную годовую ставку сложных процентов  если заданы номиналъная_ставка (годовая номинальная сложная процентная ставка
если заданы номиналъная_ставка (годовая номинальная сложная процентная ставка  и кол_пер
и кол_пер  количество периодов в году, за которые начисляются сложные проценты). В примере 19 ЭФФЕКТ
количество периодов в году, за которые начисляются сложные проценты). В примере 19 ЭФФЕКТ 
Задача 36.
Найдем годовую номинальную сложную процентную ставку (проценты начисляются каждый месяц), эквивалентную сложной процентной ставке  годовых. Здесь
годовых. Здесь  Тогда
Тогда 
 (= 14,1% годовых).
(= 14,1% годовых).
Вместо начисления один раз в год 15% можно начислять каждый месяц =» 14,1%/12 – 1,175%. От этого наращенная сумма не изменится.
Задача 37.
Найти годовую номинальную сложную процентную ставку (проценты начисляются каждые полгода), эквивалентную сложной процентной ставке  годовых.Замечание 1. Мастер функций
годовых.Замечание 1. Мастер функций  пакета Excel содержит финансовую функцию НОМИНАЛ (NOMINAL)
пакета Excel содержит финансовую функцию НОМИНАЛ (NOMINAL)  – финансовые – НОМИНАЛ), которая возвращает годовую номинальную сложную процентную ставку
– финансовые – НОМИНАЛ), которая возвращает годовую номинальную сложную процентную ставку  если заданы эффект_ставка (эффективная годовая ставка сложных процентов ) и кол_пер
если заданы эффект_ставка (эффективная годовая ставка сложных процентов ) и кол_пер  количество периодов в году, за которые начисляются сложные проценты). В примере 20 НОМИНАЛ
количество периодов в году, за которые начисляются сложные проценты). В примере 20 НОМИНАЛ 
Замечание 2. Аналогично рассмотренным методом можно найти эквивалентные ставки для различных вариантов процентных и учетных ставок.
Возможно, вас также заинтересует эта ссылка:
Задача 4.
Первоначальная сумма  наращенная сумма
наращенная сумма  период начисления
период начисления  года.
года.
Тогда простая процентная ставка
Задача 5.
Первоначальная сумма  наращенная сумма
наращенная сумма  период начисления
период начисления  года. Найти простую процентную ставку.
года. Найти простую процентную ставку.
Задача 6.
Наращенная сумма  период начисления
период начисления  года (один квартал), простая процентная ставка
года (один квартал), простая процентная ставка  годовых.
годовых.
Тогда первоначальная сумма
Задача 7.
Наращенная сумма  период начисления
период начисления  года, простая процентная ставка
года, простая процентная ставка  годовых. Найти первоначальную сумму.
годовых. Найти первоначальную сумму.
Задача 8.
Первоначальная сумма  помещена в банк под
помещена в банк под  годовых (проценты простые) на срок с 18 марта 2003 года по 20 октября 2003 года. Найдем наращенную сумму в каждой из практик начисления процентов.В немецкой практике начисления процентов продолжительность года
годовых (проценты простые) на срок с 18 марта 2003 года по 20 октября 2003 года. Найдем наращенную сумму в каждой из практик начисления процентов.В немецкой практике начисления процентов продолжительность года  дней,
дней,  (март)
(март)  (апрель, май, июнь, июль, август, сентябрь) 20 (октябрь) — 1 (день открытия и день закрытия счета всегда считаются за один день) = 213 дней. Тогда
(апрель, май, июнь, июль, август, сентябрь) 20 (октябрь) — 1 (день открытия и день закрытия счета всегда считаются за один день) = 213 дней. Тогда 
 Во французской практике продолжительность года
Во французской практике продолжительность года  дней,
дней,  (март) 30 (апрель) 31 (май) 30 (июнь) 31 (июль) 31 (август) 30 (сентябрь) 20 (октябрь) – 1 (день открытия и день закрытия счета всегда считаются за один день) – 216 дней. Тогда
(март) 30 (апрель) 31 (май) 30 (июнь) 31 (июль) 31 (август) 30 (сентябрь) 20 (октябрь) – 1 (день открытия и день закрытия счета всегда считаются за один день) – 216 дней. Тогда 
 В английской практике продолжительность года
В английской практике продолжительность года  365 дней,
365 дней,  216 дней. Тогда
216 дней. Тогда 

Задача 9.
Первоначальная сумма  руб. помещена в банк под
руб. помещена в банк под  годовых (проценты простые) на срок с 19 февраля 2003 года по 27 ноября 2003 года. Найти наращенную сумму в каждой из практик начисления процентов.
годовых (проценты простые) на срок с 19 февраля 2003 года по 27 ноября 2003 года. Найти наращенную сумму в каждой из практик начисления процентов.
Задача: решение задач по макроэкономике
Задача №17
ВНП = 5000 ден. ед. Потребительские расходы составляют 3200 ден. ед., государственные расходы равны 900 ден. ед., а чистый экспорт равен 80 ден. ед.
Рассчитать:
1. Величину инвестиций.
2. Объем импорта при условии, что экспорт равен 350 ден. ед.
3. ЧНП при условии, что сумма амортизации составляет 150 ден. ед.
4. В этой задаче чистый экспорт выражается положительной величиной. Может ли она быть отрицательной? В каком случае?
Решение:
1. Инвестиции =
ВНП (5000 ден. ед.)
— потребительские расходы (3200 ден. ед.)
— государственные расходы (900 ден. ед.)
— чистый экспорт (80 ден. ед.)
=5000-3200-900-80=820 ден. ед.
2. Импорт =
экспорт (350 ден. ед.)
— чистый экспорт (80 ден. ед.)
=350-80=270 ден. ед.
3. ЧНП=
ВНП (5000 ден. ед.)
— амортизация (150 ден. ед.)
=5000-150=4850 ден. ед.4. Чистый экспорт может выражаться отрицательной величиной, если импорт превышает экспорт.
Термины, встречающиеся в задаче:
Амортизация – это ежегодные отчисления, равные стоимости потребленного за этот период капитала.
Валовой национальный продукт (ВНП) – это общая стоимость всех конечных товаров и услуг, произведенных в стране в течение года.
Валовые частные внутренние инвестиции – это затраты на вновь произведенные средства производства (машины, станки, оборудование, здания), предназначенные для производственного процесса и пополнения товарно-материальных запасов.
Государственные закупки товаров и услуг – это все расходы государства на конечную продукцию и услуги (они не включают трансфертные платежи).
Импорт – это приобретение у иностранного контрагента товара с ввозом его в страну из за границы.
Чистые инвестиции – это валовые инвестиции минус амортизация.
Чистый национальный продукт (ЧНП) – это валовой национальный продукт, уменьшенный на сумму амортизационных отчислений.
Чистый экспорт – это экспорт товаров и услуг минус импорт товаров и услуг.
Экспорт – это вывоз товаров, капитала и услуг за границу для реализации на внешних рынках.
Задача №140
Между предприятиями-изготовителями установились определенные хозяйственные связи. Первое предприятие продало свою продукцию второму предприятию на сумму 10 млн. ден. ед., а остальную продукцию реализовало на рынке за 20 млн. ден. ед. Второе и третье предприятия поставили четвертому предприятию продукцию соответственно на 50 и 100 млн. ден. ед.; четвертое – пятому на сумму 400 млн. ден. ед. Пятое предприятие, реализовав свою продукцию на рынке, получило 700 млн. ден. ед.
Рассчитайте величину конечного (КП) и промежуточного (ПП) продукта, а также размер валового внутреннего продукта (ВВП), созданного этими предприятиями.
Решение:
Валовой внутренний продукт – это конечный продукт (КП), произведенный хозяйствующими субъектами внутри страны за определенный период времени (год, квартал, месяц). Этот показатель отражает оценку текущего производства конечных товаров и услуг (не включает продукт перепродажи, а также стоимость промежуточного продукта). ВВП произведен внутри страны собственным и иностранным капиталом, функционирующим на ее территории. Поэтому величина ВВП, произведенная на данных пяти предприятиях, равна 720 млн. ден. ед. (20 700) – стоимости их товара, поступившего на рынок.
Весь производственный общественный продукт, или валовой общественный продукт (ВОП), – также результат деятельности всех предприятий, но он образуется как сумма их продуктов и услуг и включает в себя промежуточный продукт. Следовательно, произведенный всеми предприятиями ВОП равен 1280 млн. ден. ед. (20 10 50 100 400 700).
Верно соотношение: ВОП=КП ПП. Стоимость конечного продукта, как это нами уже выяснено, равна стоимости ВВП, т.е. 720 млн. ден. ед.
Стоимость промежуточного продукта (ПП) можно найти либо как разницу ВОП — КП, либо суммируя стоимости продуктов предприятии, поступающих на другие предприятия для дальнейшей их переработки. В нашем случае ПП равен 560 млн. ден. ед. (10 50 100 400).
КП равен ВОП минус ПП, т.е. 1280 — 560 = 720 млн. ден. ед.
Задача №141
Рассчитайте величину ВНП на основании приведенных ниже показателей.
82
Дивиденды (распределенная прибыль)
96
Чистый процент (сумма процентных платежей предприятий за вычетом суммы полученных ими процентов плюс суммы процентов поступлений от экономических агентов других стран)
467
Стоимость износа основного капитала (амортизационные отчисления)
60
Косвенные налоги на бизнес
58
Прочие выплаты
0,5
Контрольная – решенные задачи по инвестициям
20 страниц. Интеллектуальные инвестиции Проектирование инвестиций Задача Список использованной литературы На предприятии оценивают два инвестиционных проекта. Эти проекты являются взаимоисключающими, поскольку предполагается использование одних и тоже производственных площадей, хотя ограничения на инвестиции отсутствуют. Год Проект ВВ, тис. грн. Проект ОВ, тис. грн. 0 350,0 550,0 1-й год 150,0 250,0 2-й год 150,0 250,0 3-й год 150,0 250,0 Диско…
Математическое дисконтирование
Математическим дисконтированием называется операция, когда по наращенной сумме  периоду начисления
периоду начисления  и сложной процентной ставке
и сложной процентной ставке  нужно определить первоначальную сумму
нужно определить первоначальную сумму  Это делается следующим образом:
Это делается следующим образом: 

Нахождение эквивалентной номинальной сложной процентной ставки для сложной процентной ставки
Выразив из равенства  ставку
ставку  через
через 
 мы найдем эквивалентную номинальную ставку сложных процентов (проценты начисляются
мы найдем эквивалентную номинальную ставку сложных процентов (проценты начисляются  раз в году) для сложной процентной ставки
раз в году) для сложной процентной ставки  Формула не зависит от периода начисления
Формула не зависит от периода начисления 
Нахождение эквивалентной простой процентной ставки для номинальной сложной процентной ставки
Пусть  — первоначальная сумма,
— первоначальная сумма,  — период начисления. При использовании простой процентной ставки
— период начисления. При использовании простой процентной ставки  наращенная сумма
наращенная сумма  При использовании номинальной сложной процентной ставки
При использовании номинальной сложной процентной ставки  (проценты за год начисляются
(проценты за год начисляются  раз) наращенная сумма
раз) наращенная сумма  Так как ставки эквивалентны, то наращенные суммы равны:
Так как ставки эквивалентны, то наращенные суммы равны:  то есть
то есть  Отсюда
Отсюда 
Нахождение эквивалентной простой процентной ставки для сложной процентной ставки
Пусть  — первоначальная сумма,
— первоначальная сумма,  — период начисления. При использовании простой процентной ставки
— период начисления. При использовании простой процентной ставки  наращенная сумма
наращенная сумма  При использовании сложной процентной ставки
При использовании сложной процентной ставки  наращенная сумма
наращенная сумма  Так как ставки эквивалентны, то наращенные суммы равны:
Так как ставки эквивалентны, то наращенные суммы равны:  Отсюда
Отсюда 

Нахождение эквивалентной сложной процентной ставки для номинальной сложной процентной ставки.
ЭФФЕКТИВНАЯ СЛОЖНАЯ ПРОЦЕНТНАЯ СТАВКА
Пусть  — первоначальная сумма,
— первоначальная сумма,  — период начисления. При использовании сложной процентной ставки
— период начисления. При использовании сложной процентной ставки  наращенная сумма
наращенная сумма  При использовании номинальной сложной процентной ставки
При использовании номинальной сложной процентной ставки  (проценты за год начисляются
(проценты за год начисляются  раз) наращенная сумма
раз) наращенная сумма  Так как ставки эквивалентны, то наращенные суммы равны:
Так как ставки эквивалентны, то наращенные суммы равны:  Отсюда
Отсюда  Эта формула определяет эффективную годовую ставку сложных процентов, эквивалентную номинальной сложной процентной ставке, и не зависит от периода начисления
Эта формула определяет эффективную годовую ставку сложных процентов, эквивалентную номинальной сложной процентной ставке, и не зависит от периода начисления 
Начисление сложных процентов несколько раз в году. номинальная процентная ставка
Начисление сложных процентов может происходить несколько раз в году. В этом случае указывают номинальную процентную ставку  на основании которой рассчитывают процентную ставку для каждого интервала начисления.Если в году
на основании которой рассчитывают процентную ставку для каждого интервала начисления.Если в году  интервалов начисления, то на каждом из них процентная ставка равна
интервалов начисления, то на каждом из них процентная ставка равна  Тогда наращенная сумма
Тогда наращенная сумма  Аналогично вышесказанному из этой формулы можно выразить любую величину через остальные:
Аналогично вышесказанному из этой формулы можно выразить любую величину через остальные:
Непрерывное начисление сложных процентов
 Устремим продолжительность интервала начисления к нулю, то есть
Устремим продолжительность интервала начисления к нулю, то есть  Это непрерывное начисление сложных процентов. Тогда
Это непрерывное начисление сложных процентов. Тогда 

 ( второй замечательный предел). Тогда
( второй замечательный предел). Тогда  Отсюда
Отсюда 
Ответы на вопросы по заказу заданий по инвестициям:
 Сколько стоит помощь?
Сколько стоит помощь?
- Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам – я изучу и оценю.
 Какой срок выполнения?
Какой срок выполнения?
- Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.
 Если требуется доработка, это бесплатно?
Если требуется доработка, это бесплатно?
- Доработка бесплатна. Срок выполнения от 1 до 2 дней.
 Могу ли я не платить, если меня не устроит стоимость?
Могу ли я не платить, если меня не устроит стоимость?
- Оценка стоимости бесплатна.
 Каким способом можно оплатить?
Каким способом можно оплатить?
- Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.
 Какие у вас гарантии?
Какие у вас гарантии?
- Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.
 В какое время я вам могу написать и прислать задание на выполнение?
В какое время я вам могу написать и прислать задание на выполнение?
- Присылайте в любое время! Я стараюсь быть всегда онлайн.
Содержание:
- Ответы на вопросы по заказу заданий по инвестициям:
- Задача 1.
- Задача 2.
- Задача 3.
- Задача 4.
- Задача 5.
- Математическое дисконтирование
- Задача 6.
- Задача 7.
- Английская, немецкая и французская практики начисления процентов
- Задача 8.
- Задача 9.
- Случай изменения простой ставки ссудного процента
- Задача 10.
- Задача 11.
- Сложные ставки ссудных процентов
- Задача 12.
- Задача 13.
- Задача 14.
- Задача 15.
- Задача 16.
- Задача 17.
- Математическое дисконтирование
- Задача 18.
- Задача 19.
- Случай, когда период начисления не является целым числом
- Задача 20.
- Задача 21.
- Задача 22.
- Задача 23.
- Случай изменения сложной ставки ссудного процента
- Задача 24.
- Задача 25.
- Начисление сложных процентов несколько раз в году. номинальная процентная ставка
- Задача 26.
- Задача 27.
- Непрерывное начисление сложных процентов
- Задача 28.
- Задача 29.
- Нахождение эквивалентной простой процентной ставки для сложной процентной ставки
- Задача 30.
- Задача 31.
- Нахождение эквивалентной простой процентной ставки для номинальной сложной процентной ставки
- Задача 32.
- Задача 33.
- Нахождение эквивалентной сложной процентной ставки для номинальной сложной процентной ставки.
- Задача 34.
- Задача 35.
- Нахождение эквивалентной номинальной сложной процентной ставки для сложной процентной ставки
- Задача 36.
- Задача 37.
Инвестиции – достаточно новое понятие для российской экономики. В централизованной плановой системе использовалось понятие «валовые капитальные вложения» – под ними подразумевались все затраты на воспроизводство основных фондов, включая затраты на их полное восстановление; они рассматривались тождественно инвестициям.
С принятием в 1991 г. Закона РФ «Об инвестиционной деятельности в РСФСР» под инвестициями стали понимать денежные средства, целевые банковский вклады, паи, акции и другие ценные бумаги, технологии, машины, оборудование, лицензии (в том числе на товарные знаки), кредиты, любое другое имущество или имущественные права, интеллектуальные ценности, вкладываемые в объекты предпринимательской и другой деятельности в целях получения прибыли (дохода) и достижения положительного социального эффекта.
Возможно, вас также заинтересует эта ссылка:
Простые ставки ссудных процентов
Пусть  — первоначальная сумма,
— первоначальная сумма,  — наращенная сумма,
— наращенная сумма,  — годовая процентная ставка (проценты простые). Так как проценты простые, то в течение всего периода начисления они применяются к первоначальной сумме
— годовая процентная ставка (проценты простые). Так как проценты простые, то в течение всего периода начисления они применяются к первоначальной сумме  Предположим, что первоначальная сумма
Предположим, что первоначальная сумма  была помещена в банк под
была помещена в банк под  процентов годовых (проценты простые).Прошел 1 год. Тогда наращенная сумма
процентов годовых (проценты простые).Прошел 1 год. Тогда наращенная сумма  (первоначальная сумма)
(первоначальная сумма)  (проценты) =
(проценты) =  Прошел еще 1 год (то есть вклад лежит уже 2 года). Тогда наращенная сумма после двух лет
Прошел еще 1 год (то есть вклад лежит уже 2 года). Тогда наращенная сумма после двух лет  (наращенная сумма после одного года)
(наращенная сумма после одного года)  (проценты) =
(проценты) =  Прошел еще 1 год (то есть вклад лежит уже 3 года). Тогда наращенная сумма после трех лет
Прошел еще 1 год (то есть вклад лежит уже 3 года). Тогда наращенная сумма после трех лет  (наращенная сумма после двух лет)
(наращенная сумма после двух лет)  (проценты) =
(проценты) =  И т. д.Если
И т. д.Если  — период начисления процентов (в годах), то наращенная сумма через
— период начисления процентов (в годах), то наращенная сумма через  лет
лет  Пример 1. Первоначальная сумма
Пример 1. Первоначальная сумма  руб. помещена в банк на
руб. помещена в банк на  года под
года под  годовых (проценты простые).Тогда наращенная сумма после двух лет
годовых (проценты простые).Тогда наращенная сумма после двух лет 

Возможно, вас также заинтересует эта ссылка:
Проанализируйте предложенную таблицу
(данные гипотетические).
Год | Номинальный ( | Дефлятор ( в % ) | Реальный (млрд. |
1 2 3 4 5 — й | 1800 2400 3500 4200 6000 | 50 70 100 105 120 |
Дайте
ответы на следующие вопросы:
1.
Показателем чего является номинальный ВНП?
2. В чем отличие реального ВНП от
номинального ВНП?
3. Что такое дефлятор и как его можно
рассчитать?
4. Заполните последний столбец таблицы.
Решение:
1. Валовой
национальный продукт – это годовая рыночная стоимость всех товаров и услуг,
произведенных национальной экономикой для конечного потребления за год. ВНП
измеряет стоимость продукции, произведенной факторами производства,
находящимися в собственности граждан данной страны, в том числе и на
территории других стран. Главный показатель экономического состояния
производственной сферы страны.
2. Номинальный ВНП
– это валовой национальный продукт, стоимость которого выражена в текущих,
фактических ценах. Взятый в динамике, он одновременно отражает изменение как
физического объёма продукта, так и уровня цен. Следовательно, в условиях
инфляции он завышает результаты экономической деятельности, требует корректировки.
Реальный ВНП – это
валовой национальный продукт, стоимость которого скорректирована на величину
годового роста цен. Таким образом: номинальный ВНП дает обобщающую денежную
оценку произведенной народным хозяйством страны продукции; реальный ВНП
характеризует количество произведенной продукции, т.е. объём производства
измеренный в постоянных ценах (ценах базисного года).
3. Дефлятор
показывает изменение уровня цен произведенной продукции в текущем году по
отношению к базисному году.
Дефлятор ВНП =
где — цены единицы i – го вида
товара в базисном и текущем
периоде времени соответственно;
—
количество товара i–го вида, реализованное в текущем году.
Следовательно, номинальный
ВНП
Реальный
ВНП = ——————————дефлятор
Реальный ВНП составил в:
1–м году 1800 млрд. ден.
ед.: 0,5 = 3600 млрд. ден. ед.
2-ом году 2400 млрд. ден.
ед.: 0,7 = 4000 млрд. ден. ед.
3-ем году 3500 млрд. ден.
ед.: 1 = 3500 млрд. ден. ед.
4-ом году 4200 млрд. ден.
ед.: 1,05 = 4000 млрд. ден. ед.
5-ом году 6000 млрд. ден.
ед.: 1,2 = 5000 млрд. ден. ед.
ТЕМА 2.НАЦИОНАЛЬНЫЙ РЫНОК И ЕГО РАВНОВЕСИЕ.
Решение задач по инвестиционному анализу 2
Ниже приведены условия и решения задач. Закачка решений в формате doc и mcd начнется автоматически через 10 секунд.
Задача №1
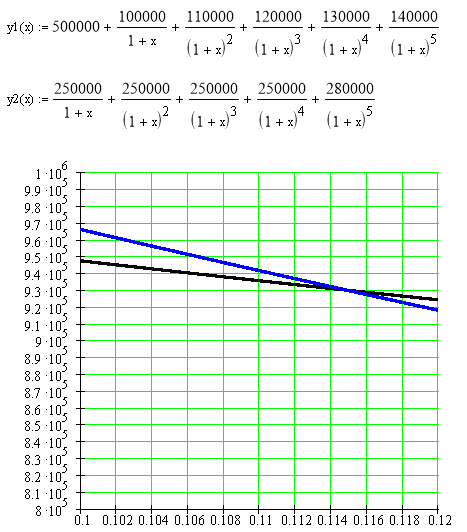
Предприятие собирается приобрести оборудование, чтобы самостоятельно производить детали, которые раньше покупали от поставщиков. Стоимость оборудования — 500000. Эксплуатационные расходы в первый год составляют100000 и ежегодно возрастают на 10000. За поставку деталей ежегодно платили поставщикам по 250000. Срок эксплуатации оборудования – 5 лет. Ликвидационная стоимость – 30000 (чистый доход от продажи оборудования в конце 5-го года). Ставка по альтернативным проектам- 8% годовых. Эффективна ли данная инвестиция (NPV, PI, IRR, MIRR, PP, PPD)? Дайте письменное заключение о целесообразности реализации проекта.
Решение.
Период | Отток средств | Приток средств | Поток платежей | Коэффициент дисконтирования | Дисконтированный поток платежей | ||
(t) | Kt | Dt | (CFt) |
| DCFt | Kt·t | Dt·t |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
0 | -500000 | 0 | -500000 | 1 | -500000 | -500000 | 0 |
1 | -100000 | 250000 | 150000 | 0,92593 | 138888,889 | -92593 | 231481 |
2 | -110000 | 250000 | 140000 | 0,85734 | 120027,435 | -94307 | 214335 |
3 | -120000 | 250000 | 130000 | 0,79383 | 103198,191 | -95260 | 198458 |
4 | -130000 | 250000 | 120000 | 0,73503 | 88203,5823 | -95554 | 183757 |
5 | -140000 | 280000 | 140000 | 0,68058 | 95281,6476 | -95282 | 190563 |
Итого | – | – | – | – | 45599,745 | -972995 | 1018595 |
Для проекта определяем приведенную стоимость поступлений от инвестиций по формуле:
![]()
, где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
NPV = 31443,6
Определим индекс прибыльности.
ИД определим по формуле:
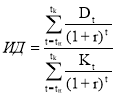
Индекс прибыльности:
PI = 1018595/972995 = 1,047
Внутренняя норма доходности (IRR) – это такая норма дисконта, при которой сумма дисконтированных доходов за жизненный цикл проекта равна сумме дисконтированных инвестиций.
Определим внутреннюю норму доходности для каждого из проектов.
Для первого проекта решим уравнение:
∑ CFk / ( 1 IRR )k = ∑ INVt / (1 IRR) t
![]()
Решим уравнение аналитически, методом подбора.
Следовательно, IRR = 0,115.
Определим срок окупаемости для проектас учетом дисконтирования.
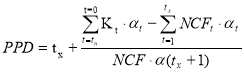
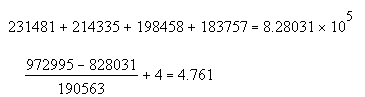
PPD = 4,761.
При ставке сравнения 8% имеет смысл инвестировать средства в данный проект, имеем положительный чистый дисконтированный доход, индекс доходности 104,7%. Однако при увеличении инфляции свыше 11,5% не имеет смысла инвестировать средства в данный проект (IRR=0,115), так же срок окупаемости проекта достаточно высокий и составляет 4,761 года, и близок к эксплуатационному сроку работы оборудования.
Задача №2
Фирма «Смирнов и Андрианов» покупает завод по производству глиняной посуды за 100 млн.рублей. Кроме того расчёты показывают, что для модернизации этого предприятия в первый же год потребуются дополнительные затраты в 50 млн. рублей. Однако, при этом предполагается, что в последующие 9 лет этот завод будет обеспечивать ежегодные денежные поступления по 25 млн. рублей. Затем, через 10 лет, предполагается, что фирма продаст завод по остаточной стоимости, которая составит согласно расчётам 80 млн. рублей. Средняя ставка доходности 10%. Эффективна ли данная инвестиция (NPV, PI, IRR, MIRR, PP, PPD)? Дайте письменное заключение о целесообразности реализации проекта
Решение.
Период | Отток средств | Приток средств | Поток платежей | Коэффициент дисконтирования | Дисконтированный поток платежей | ||
(t) | Kt | Dt | (CFt) |
| DCFt | Kt·t | Dt·t |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
0 | -100 | 0 | -100 | 1 | -100 | -100 | 0 |
1 | -50 | 25 | -25 | 0,90909091 | -22,7272727 | -45,455 | 22,7273 |
2 | 25 | 25 | 0,82644628 | 20,661157 | 0 | 20,6612 | |
3 | 25 | 25 | 0,7513148 | 18,78287 | 0 | 18,7829 | |
4 | 25 | 25 | 0,68301346 | 17,0753364 | 0 | 17,0753 | |
5 | 25 | 25 | 0,62092132 | 15,5230331 | 0 | 15,523 | |
6 | 25 | 25 | 0,56447393 | 14,1118483 | 0 | 14,1118 | |
7 | 25 | 25 | 0,51315812 | 12,828953 | 0 | 12,829 | |
8 | 25 | 25 | 0,46650738 | 11,6626845 | 0 | 11,6627 | |
9 | 105 | 105 | 0,42409762 | 44,5302499 | 0 | 44,5302 | |
Итого | – | – | – | – | 32,4488594 | -145,45 | 177,903 |
Для проекта определяем приведенную стоимость поступлений от инвестиций по формуле:
![]()
, где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
NPV = 3245
Определим индекс прибыльности.
ИД определим по формуле:
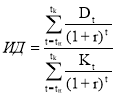
Индекс прибыльности:
PI = 177,9/145,45 = 1,223
Внутренняя норма доходности (IRR) – это такая норма дисконта, при которой сумма дисконтированных доходов за жизненный цикл проекта равна сумме дисконтированных инвестиций.
Определим внутреннюю норму доходности для каждого из проектов.
Для первого проекта решим уравнение:
∑ CFk / ( 1 IRR )k = ∑ INVt / (1 IRR) t
Решим уравнение аналитически, методом подбора.
Следовательно, IRR = 0,147.
Определим срок окупаемости для проектас учетом дисконтирования.
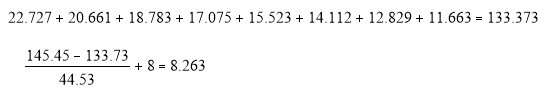
PPD = 8,263.
При ставке сравнения 10% имеет смысл инвестировать средства в данный проект, имеем положительный чистый дисконтированный доход, индекс доходности 122,3%. Однако при увеличении инфляции свыше 14,7% не имеет смысла инвестировать средства в данный проект (IRR=0,147), так же срок окупаемости проекта достаточно высокий и составляет 8,263 года, и близок к эксплуатационному сроку работы оборудования.
Задача №3
Городской мясокомбинат планирует приобрести ещё один холодильник, для чего сначала необходимо подготовить помещение. Эти подготовительные работы займут год и составят в денежном выражении 5 млн.р. Сама же холодильная камера будет куплена в конце этого года за 30 млн.р. и будет эксплуатироваться 3 года. Денежные поступления соответственно составят 10, 15 и 20 млн.р. Требуемый уровень доходности – 10%.
Эффективна ли данная инвестиция (NPV, PI, IRR, MIRR, PP, PPD)? Дайте письменное заключение о целесообразности реализации проекта
Решение.
Период | Отток средств | Приток средств | Поток платежей | Коэффициент дисконтирования | Дисконтированный поток платежей | ||
(t) | Kt | Dt | (CFt) |
| DCFt | Kt·t | Dt·t |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
0 | -5 | 0 | -5 | 1 | -5 | -5 | 0 |
1 | -30 | 10 | -20 | 0,90909091 | -18,1818182 | -27,27 | 9,09091 |
2 | 0 | 15 | 15 | 0,82644628 | 12,3966942 | 0 | 12,3967 |
3 | 0 | 20 | 20 | 0,7513148 | 15,026296 | 0 | 15,0263 |
Итого | – | – | – | – | 4,24117205 | -32,27 | 36,5139 |
Для проекта определяем приведенную стоимость поступлений от инвестиций по формуле:
![]()
, где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
NPV =4,24
Определим индекс прибыльности.
ИД определим по формуле:
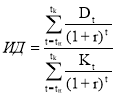
Индекс прибыльности:
PI = 36,51/32,27 = 1,131
Внутренняя норма доходности (IRR) – это такая норма дисконта, при которой сумма дисконтированных доходов за жизненный цикл проекта равна сумме дисконтированных инвестиций.
Определим внутреннюю норму доходности для каждого из проектов.
Для первого проекта решим уравнение:
∑ CFk / ( 1 IRR )k = ∑ INVt / (1 IRR) t
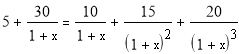
Решим уравнение аналитически, методом подбора.
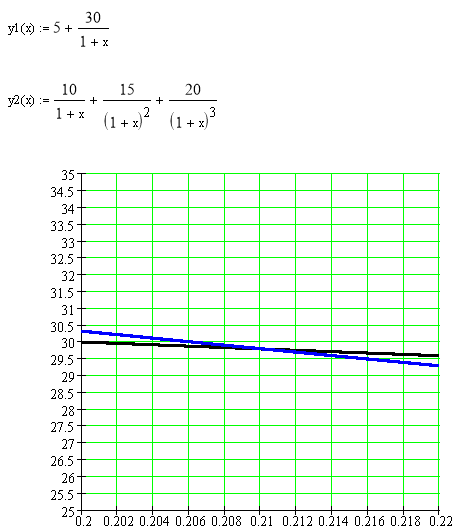
Следовательно, IRR = 0,21.
Определим срок окупаемости для проектас учетом дисконтирования.
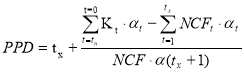
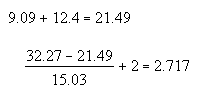
PPD = 2,717.
При ставке сравнения 10% имеет смысл инвестировать средства в данный проект, имеем положительный чистый дисконтированный доход, индекс доходности 131,1%. Однако при увеличении инфляции свыше 21% не имеет смысла инвестировать средства в данный проект (IRR=0,21).Cрок окупаемости проекта составляет 2,717 года.
Решение:
Исходя из данных, приведенных в условии
задачи можно рассчитать ВНП по расходам:
У = С І G
Х, гдеG– государственные
закупки товаров и услуг.
У – ВНП, С – потребительские расходы,
І – валовые инвестиции;
Хn– чистый
экспорт.
ВНП = 77,2 16,2 8,5 1,1;
У = 103 (млрд. ден. ед.)
ЧНП = ВНП – А = 103 – 7,9 = 95,1(млрд.ден.ед.)
НД = ЧНП – косвенные налоги:
НД = 95,1 – 7 = 88,1(млрд.ден.ед.)
ЛД = НД – взносы на социальное страхование
– нераспределенная прибыл – налоги
на прибыль корпораций трансфертные
платежи
ЛД = 88,1 – 0,2 – 2,8 – 1,4 4,0 = 87,7(млрд.ден.ед.)
ЛРД = ЛД – подоходные налоги
ЛРД = 87,7 – 2,6 = 85,1(млрд.ден.ед.)
Ответ: ВНП = 103 млрд.ден.ед.; ЧНП = 95,1
млрд.ден.ед.; НД = 88,1 млрд.ден.ед.; ЛД = 88,7
млрд.ден.ед.; ЛРД = 85,1 млрд.ден.ед.
studfiles.net
Сложные ставки ссудных процентов
Пусть  — первоначальная сумма,
— первоначальная сумма,  — наращенная сумма,
— наращенная сумма,  — годовая процентная ставка (проценты сложные). Так как проценты сложные, то в конце каждого интервала начисления процентная ставка применяется к наращенной сумме на начало этого интервала начисления.Предположим, что первоначальная сумма
— годовая процентная ставка (проценты сложные). Так как проценты сложные, то в конце каждого интервала начисления процентная ставка применяется к наращенной сумме на начало этого интервала начисления.Предположим, что первоначальная сумма  была помещена в банк под
была помещена в банк под  процентов годовых (проценты сложные).
процентов годовых (проценты сложные).
Прошел 1 год. Тогда наращенная сумма  (сумма на начало этого интервала начисления)
(сумма на начало этого интервала начисления)  (проценты) =
(проценты) = 
Прошел еще 1 год (то есть вклад лежит уже 2 года). Тогда наращенная сумма после двух лет  (наращенная сумма после одного года)
(наращенная сумма после одного года)  (проценты) =
(проценты) =  Прошел еще 1 год (то есть вклад лежит уже 3 года). Тогда наращенная сумма после трех лет
Прошел еще 1 год (то есть вклад лежит уже 3 года). Тогда наращенная сумма после трех лет  (наращенная сумма после двух лет)
(наращенная сумма после двух лет)  (проценты) =
(проценты) =  И т. д.Если
И т. д.Если  — период начисления процентов (в годах), то наращенная сумма через
— период начисления процентов (в годах), то наращенная сумма через  лет
лет 
Случай изменения простой ставки ссудного процента
Пусть на интервалах начисления (в годах)  применялись простые процентные ставки
применялись простые процентные ставки  соответственно. Тогда наращенная сумма
соответственно. Тогда наращенная сумма 

Случай изменения сложной ставки ссудного процента
Пусть на интервалах начисления (в годах)  применялись сложные процентные ставки
применялись сложные процентные ставки  соответственно.Тогда наращенная сумма
соответственно.Тогда наращенная сумма 

Случай, когда период начисления не является целым числом
Если период начисления  не является целым числом, то формула
не является целым числом, то формула  дает приблизительный (и весьма неточный) результат. Поэтому используют другой подход.Определение. Целая часть
дает приблизительный (и весьма неточный) результат. Поэтому используют другой подход.Определение. Целая часть  числа
числа  — это наибольшее целое число, не превосходящее
— это наибольшее целое число, не превосходящее 
Тема 1. макроэкономические показатели
Государственный
стандарт экономического образования
предусматривает усвоение студентами
высших учебных заведений России не
только теоретического, но практического
материала по курсу «Экономическая
теория».
Настоящее
издание представляет собой сборник
задач с ответами и описанием решений,
а также рекомендуемой литературы по
разделу «Макроэкономика». Материал
задачника расположен в соответствии с
темами программы изучаемого курса.
Предлагаемые
в данном издании задачи, отражают опыт
преподавания курса экономической теории
на кафедре экономики и маркетинга МГТУ
им. Г. И. Носова и ориентированы в первую
очередь на студентов заочной формы
обучения, позволит им самим выяснить,
насколько глубоко они усвоили предмет.
Задача
1. По данным
таблицы рассчитайте:
а) объём ВНП по потоку
расходов;
б) объём ВНП по потоку
доходов;
в) объём ЧНП;
г) объём НД.
Счёт | Млрд. |
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. | 10 20 105 150 1000 340 400 25 610 3000 410 500 3300 |
Решение:
а)
Исходя из основного макроэкономического
тождества: ВНП (Y)
= С I G
Xn,
где
С — потребительские
расходы,
G
— государственные
закупки товаров и услуг,
I
— инвестиции
валовые,
Xn — чистый экспорт.
Складываем
показатели потребительских расходов
(3 300), валовых инвестиций (610), государственных
закупок (1 000) и чистого экспорта (20).
Получим ВНП по расходам = 4 930 млрд. ден.
ед.
б)
ВНП по доходам определяем путем сложения
нераспределенной прибыли корпораций
(10), дивидендов (105), налогов на прибыль
корпораций (10), доходов от индивидуальных
вложений (340), процентов (400), арендной
платы (25), заработной платы наемных
работников (3 000) косвенных налогов на
бизнес (400), объёма потребленного капитала
(амортизации) (500). Получаем ВНП по доходам
= 4 930 млрд. ден. ед. ВНП по расходам равен
ВНП по доходам.
в)
ЧНП = ВНП – амортизация;
ЧНП
= 4 930 – 500 = 4 430 млрд. ден. ед.;
г)
НД = ЧНП – косвенные налоги на бизнес;
НД
= 4 430 – 400 = 4 030 млрд. ден. ед.
Задача 2.
Имеются
следующие данные по экономике
гипотетической страны за год ( млрд.
ден. ед)
Счета
млрд. ден. ед.
_________________________________________________________
Трансфертные платежи
4
Валовые внутренние
инвестиции 16
Косвенные
налоги на бизнес
7
Личные подоходные
налоги 2, 5
Чистый экспорт
1, 5
Нераспределенные
прибыли корпораций 3
Амортизация
8
Личные потребительские
расходы 78
Налоги на прибыль
корпораций 2
Взносы
на социальное страхование
0, 5
Государственные закупки
товаров и услуг 8, 5
Рассчитайте: а)
показатель ВНП,
б) личного
располагаемого дохода,
в)
величину частных сбережений (Sp).
Решение:
а) Исходя из данных приведенных в
условии задачи, можно рассчитать ВНП
по расходам (для расчета по доходам не
хватает информации).
ВНП
(Y)
= С I G
Xn; ВНП = 78 16 8,5 1,5 = 104
б)
Чтобы рассчитать величину личного
располагаемого дохода, мы должны найти
вначале чистый национальный продукт
(ЧНП), национальный доход (НД) и личный
доход (ЛД):
ЧНП = ВНП — амортизация;
ЧНП = 104 – 8 = 96
НД = ЧНП – косвенные
налоги на бизнес
НД = 96 – 7 = 89
ЛД
= НД – взносы на социальное страхование
— нераспределенная прибыль корпораций
— налоги на прибыль корпораций
трансфертные платежи.
ЛД = 89 – 05 –3 – 2 4 = 87,
5
Располагаемый личный
доход (РЛД) равен личному доходу за
вычетом подоходных налогов:
РЛД = 87, 5 – 2, 5 = 85
в)
Располагаемые личные доходы используются
на потребление, а часть превращается в
сбережения (Sp).
Следовательно, частные сбережения могут
быть получены путем вычитания личных
потребительских расходов из располагаемого
личного дохода: Sp
= РЛД – С = 85 — 78 = 7.
studfiles.net








