Экономика – решение задач с примерами и образцами выполнения (онлайн)

Задачи с решениямипофинансовойматематике

1. Банкначисляет 50 рублейобыкновенногопростогопроцентазаиспользование 3000 рублей в течение 60 дней. Какованормапростогопроцентатакойсделки?

Решение:

Простойпроцентвычисляетсяпоформуле:

R = iP * (t/T);

50 =i 3000* (60/365);

I = 365*50 /(3000*60) = 0,1014 (10,14%)

Или:

S = P (1 i); (50 3000) = 3000 (1 i); 3050 = 3000 3000 i; 50/3000 = i; i = 0,0167 (1,67 %) – за 60 дней (два месяца); за год: i = 0,0167*365/60 = 0,101388 (10,14%);

Решение:

В случаепростогодисконта:

P = S (1 – nd);

Выручка:

P = 100000 (1 – 0,035* 72/365)= 100000 *0,993 = 99300 руб.

Дисконтсоставит:

100000 – 99300 = 700 руб.

Решение:

Sn = P(1 i)n

2 = 1 (1 i)12

(1 i)12 =2

Прологарифмируемполученноевыражение:

12 lg (1 i) = lg2; lg2 = 0,3

12 lg (1 i) = 0,3

Lg (1 i) = 0,0025; (1 i) = 1, 06; i = 0,06 (6%)

Можнобылонеделатьтакихсложныхрасчетов. В учебникахпобанковскомуделу и ценнымбумагамприлагаютсятаблицы, в которыхпоказываетсябудущаястоимостьединицы при определеннойгодовойставкечерезопределенныйпериодвремени.

Единица удваивается через 12 лет при 6% годовых.

Решение:

Эквивалентная процентная ставка:

J = (1 i)m/n -1 =(1 0,05)10/3 -1;

(1 i)m = (1 j)n = (1 0,05)10

(1 j)n = (1 0,05)10 = 1,6289

Отсюда:

(1 i)3 =1,6289; (1 i) = 1,1768; i = 0,1768 ≈ 17,7%

По ставке сложного процента:

При n = 3 и 5 %

Будущая стоимость единицы: 1,1576

Sn = P(1 i)n

Р = 10000/1,6289 = 6139,11 руб.

Тогда: 6139,11*1,1576 = 7139,63 руб.

Решение:

Полагающийся аннуитет:

500 000 = R *[(1 0,015 )4*5 -1] /0,015 * (1 0,015);

(1,34685-1)/0,015* 1,015 = 23,47044;

Отсюда: R = 500000/ 23,47044= 21303,4 руб.

Решение:

По формуле обыкновенного общего аннуитета:

S = 500 * ((1 0,04)5*1 -1)/ ((1 0,04)1/4 -1 ) = 500* 0,2167/0,00985 = 11 000 руб.

Решение:

Вечная рента – это аннуитет, платежи которого продолжаются в течение неограниченного времени

Эквивалентная процентная ставка равна:

J =(1 i)m/p -1 = (1 0,03)4/12 -1= 1,0108 -1 = 0,0108

M=4; p =12

А =R/j = 1500/0,0108 = 138888,88 руб.

Годовых?

Решение:

Доход по облигации представляет собой поток периодических платежей в конце каждого года (простой аннуитет) и разовую выплату в конце всего срока действия облигации.

С=N = 100000 руб.,

Ежегодные выплаты: R = 5000 руб., i =0,03

Цена покупки:

Р = 5000* [ 1-(1 0,03)-15]/0,03 100000 (1 0,03)-15 = 5000 *(1-1/1,5580)/0,03 100000(1/1,0315) = 5000 * 11,9384 100000*0,64185 = 123877 руб.

Решение:

Рассчитаем будущюю стоимость 20000 рублей через 3 года, под 17% годовых.
FV = 20000 * (1 0,17)3 = 32032 рубля.

Ответ. Получить 35000 рублей через 3 года является более выгодным решением, при данном значении процентной ставки.

Преобразуем формулу к следующему виду:

(1 r)n = FV / PV и подставим значения;

1,14n = 20000 / 1000 = 20, отсюда n = log 1,14 20 = 22,86 года.

Ответ. 1000 рублей нарастится до 20000 рублей при 14% годовой ставке за 22,86 года.

При расчете числа лет необходимо учитывать, что в формуле подразумевается целое число лет и цифры, рассчитываемые после запятой, имеют приблизительные значения, характеризующие близость к целому значению лет.

Нарастились до 30 000 рублей, за срок вклада 5 лет?

Преобразуем формулу к следующему виду:

R = (FV / PV)1/n – 1 и подставим значения;

R = (30 000 / 10 000)1/5 – 1;

R = 0,24573 или 24,573 %.

Ответ. 10 000 рублей нарастятся до 30 000 рублей за 5 лет при ставке ссудного процента 24,573%

Решение.

Способ 1.

,

K’ = K I = 4000 44=4044,

где K – капитал или заем, за использование которого заемщик выплачивает определенный процент;

I – процентный платеж или доход, получаемый кредитором от заемщика за пользование денежной ссудой;

P – процентная ставка, показывающая сколько д. е. должен заплатить заемщик за пользование 100 ед. капитала в определенном периоде времени (за год);

D – время, выраженное в днях.

360 – число дней в году.

Способ 2.

Время t = 80/360 = 2/9.

K’ = K K×i×t = 4000(1 0.05×2/9) = 4044,

Где i – процентная ставка, выраженная в долях единицы,

T – время, выраженное в годах.

Решение

2×K = I.

2×K = K×9×g/100,

G = 2×100/9 = 22.22

14. Величина предоставленного потребительского кредита – 6000 д. е., процентная ставка – 10% годовых, срок погашения – 6 месяцев. Найти величину ежемесячной выплаты (кредит выплачивается равными долями).

Решение

Таблица – План погашения кредита (амортизационный план)

Объяснение к таблице

Месячная выплата основного долга составит:

K / m = 6000/6 = 1000.

Месячный взнос представляет собой сумму выплаты основного долга и процентного платежа для данного месяца.

Процентные платежи вычисляются по формуле:

,

Где I1 – величина процентного платежа в первом месяце;

P – годовая процентная ставка, %.

Общая величина выплат за пользование предоставленным кредитом:

=175.

Общая величина ежемесячных взносов:

=1029.

Годовых. Найти дисконт и дисконтировать величину векселя.

Решение

Так как нам известна номинальная величина векселя, дисконт, находим по формуле:

=409,

Где Kn – номинальная величина векселя;

D – число дней от момента дисконтирования до даты погашения векселя;

D – процентный ключ или дивизор (D = 3600/p = 36000/8 = 4500).

Дисконтированная величина векселя равна разности номинальной стоимости векселя и дисконта (процентного платежа):

20000 – 409 = 19591.

D) годовых. Найти конечную сумму капитала, если расчетный период составляет: а) 3 месяца; б) 1 месяц.

Решение

При декурсивном (d)расчете сложных процентов:

Kmn = K×Ip/mmn, Ip/m = 1 p/(100×m),

Где Kmn – конечная стоимость капитала через N лет при p% годовых и капитализации, проводимой M раз в год.

А) K = 20000×I2.54 = 20000×(1 10/(100×4))4 = 20000×1.104 = 22076 д. е.

Б) K = 20000×I10/1212 = 20000×(1 10/(100×12))12 = 20000×1.105 = 22094 д. е.

При антисипативном (a) способе расчета сложных процентов:

Kmn = K×Iq/mmn, Iq/m = 100m/(100m – q),

Где q – годовой прцент.

А) K = 20000×(100×4/(100×4 – 10))4 = 20000×1.107 = 22132 д. е.

Б) K = 20000×(100×12/(100×12 – 10))12 = 20000×1.106 = 22132 д. е.

Решение

= 6.779%.

Решение

Сначала для годовой процентной ставки 8% определим процентную уравнивающую ставку:

=1.9427%

Затем полученную уравнивающую ставку поместим в следующую формулу:

Svmn = u× , где rk = 1 pk/100,

Где v – число вкладов в расчетном периоде,

n – число лет,

m – число капитализаций в год.

Тогда

Rk = 1 1.9427/100 = 1.0194

S4×10 = 500× = 500×60.8157 = 30407.84 д. е.

Решение

,

U1 = u×I2%4 / III2% = 2000×1.0824 / 4.204 = 514.93 д. е.

Snm = 514.93×III2%3×4 2000 = 514.93×13.6803 2000 =
= 9044.41 д. е.

D) составляет 8%.

Решение

K0 = Kn×r-n = Kn×II8 = Kn×(1 p/100)-n = 200000×(1 8/100)-20 =
= 200000×0.21454 = 42909 д. е.,

Где r = (1 p/100) – сложный декурсивный коэффициент.

Постнумерандо, процентная ставка – 4% годовых, капитализация ежегодная.

Решение

Постнумерандо по 5000 д. е. при 8% годовых, если капитализация осуществляется каждые полгода.

Решение

При ежегодной капитализации:

C0 = a×IVpn = 5000×IV8 = 5000×6.71=33550

Решение

Таблица – План погашения займа (амортизационный план)

Пояснения к таблице

Аннуитет вычисляем по формуле:

A = K×Vpn = 20000×V2 = 20000×0.1113 = 2226.53 д. е.

Чтобы определить выплату задолженности b1, вычисляем величину процентного платежа I:

I1 = K1×p/100 = 20000×2/100 = 400 д. е.

Выплата задолженности представляет собой разницу между аннуитетом и процентным платежом:

B1 = a – I1 = 2226.53 – 400 = 1826.53 д. е.

Таким образом, после первого года долг сократится на 1826.53 д. е. Остаток долга равен:

K2 = 20000 – 1826.53 = 18173.47 д. е.

Вычислим процентный платеж на остаток долга:

I2 = 18173.47×2/100 = 363.47 д. е.

Вторая выплата составит:

B2 = a – I2 = 2226.53 – 363.47 = 1863.06 д. е.

Долг уменьшится на величину 1863.06, остаток долга составит:

K3 = 18173.47 – 1863.06 = 16310.41 д. е.

Далее

I3 = 16310.41×2/100 = 326.21 д. е.

Третья выплата задолженности составит:

B3 = a – I3 = 2226.53 – 326.21 = 1900.32 д. е.

Решение:

Вывод формулы для простой ставки процентов:

Ответ: простая ставка процентов равна 180%.

5. Кредит в размере 15 000 руб. выдан с 26.03 по 18.10 под простые 24% годовых. Определить размеры долга для различных вариантов начисления процентов.

Решение:

Размер долга:

;

1) «английская практика»: Т=365 или 366 дней.

(дней)

(руб.)

2) «французская практика»: T=360 дней.

(дней)

(руб.)

3) «германская практика»: T=360 дней.

(дня)

(руб.)

Ответ: размер долга составляет:

– согласно «английской практике»: 17 031,781 руб.;

– согласно «французской практике»: 17 060 руб.;

– согласно «английской практике»: 17 020 руб.

I квартал ссудный процент 24%, а в каждом последующем квартале процентная ставка по ссуде увеличивается на 3%. Определить сумму к возврату в банк, если ссуда выдана на год и составляет 15 000 руб.(простые проценты)

Решение:

T = 1 год = 360 дней PV = 15 000 руб. 30×3 = 90 дней

Сумма начисленных процентов:

;

Сумма к возврату:

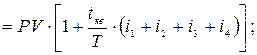
= 19 275 (руб.)

Ответ: сумма к возврату в банк составит 19 275 руб.

Решение:

PV = 15 000 руб. N = 2 года J = 16% = 0,16 M = 2

Сумма на счёте клиента к концу срока:

20 407,334 (руб.)

Ответ: сумма на счёте клиента к концу срока составит 20 407,334 руб.

Годовых. Определить дисконтированную величину, то есть сумму, полученную владельцем векселя, и величину дисконта.

Решение:

FV = 19 000 руб. T = 1 год = 360 дней T = 60 дней N = 1 год D = 60% = 0,6

Величина дисконта:

(руб.)

Сумма, полученная владельцем векселя:

PV = FV – D ;

PV = 19 000 – 1 900 = 17 100 (руб.)

Ответ:

– величина дисконта равна 1 900 руб.;

– сумма, полученная владельцем векселя, равна 17 100 руб.

N = 1 год).

Решение:

I = 24% = 0,24

N = 1 год

Эквивалентная годовая учётная ставка:

;

Ответ: эквивалентная годовая учётная ставка равна 19,4%.

Решение: FV = 19 000 руб. j = 16% = 0,16, m = 4, n = 1,5 года = года.

Сумма вклада:

15 015,976 (руб.)

Ответ: сумма вклада равна 15 015,976 руб.

Решение: N = 1 год

1) M = 4, J =24% = 0,24

2) M = 2, J =26% = 0,26

3) M = 12, J = 20% = 0,2

Эффективная процентная ставка:

при N=1 год: ;

Ответ: выдача кредитов под 26% годовых с полугодовым начислением процентов банку выгоднее, т. к. эффективная годовая процентная ставка в этом случае больше (сумма кредита возрастает на 27,7% за год).

Годовых. Полугодовой уровень инфляции составил 3%. Определить реальную годовую ставку процентов с учётом инфляции.

Решение: n = 1 год i = 24% = 0,24 = 3% = 0,03 N = 2

Индекс цен:

Реальная годовая процентная ставка:

Ответ: реальная годовая ставка процентов равна 16,9%.

Решение: = 3% = 0,03 n = 1 = 3% = 0,03 n = 1 = 10% = 0,1

Вывод формулы для процентной ставки:

Ответ: нужно назначить ставку процентов по вкладам, равную 13,3%.

Решение: N = 12 месяцев

Индекс цен:

Уровень инфляции:

Ответ: уровень инфляции за год равен 42,6%.

Решение: PV = 15 000 руб. j = 72% = 0,72 m = 12 месяцев n = 6/12 года p = 3% = 0,03,

N = 6 месяцев

Реальная покупательная способность вклада через определённое время:

(руб.)

Реальный доход вкладчика:

(руб.)

Ответ: реальный доход вкладчика равен 2 819,811 руб.

S1=19 000 руб., S2=20 000 руб., S3=21 000 руб. в конце 1-го, 3-го и 5-го годов. По новому графику платежей вносится две суммы: S4=22 000 руб. в конце 2-го года и S5 в конце 4-го года. Ставка банковского процента 5%. Определить S5.

Дано:

Суммы платежей,

S1=19 000S4 =22 000S2=20 000S5 – ?S3=21 000 руб.

|__________|__________|__________|__________|__________|

0 1 2 3 4 5 Сроки платежей,

Годы

наращение дисконтирование

На рис. отмечены: Полужирным шрифтом – исходный график платежей, Курсивом – новый график платежей. Моментом приведения выбран год, совпадающий с годом платежа суммы : : 4 года.

Решение:

Уравнение эквивалентности: графики платежей будут эквивалентны, если сумма приведённых на какую-либо дату (на момент приведения) платежей одного графика будет равна сумме платежей другого графика, приведённых на ту же дату при неизменной ставке процентов:

Коэффициент приведения (наращения или дисконтирования):

Где: N – число лет до момента приведения:

N = N0 – Ni,

Где: Ni – срок I-го платежа.

При – коэффициент наращения;

При – коэффициент дисконтирования;

При

(руб.)

Ответ: сумма второго платежа по новому графику платежей равна 38 739,875 руб.

Решение: i = 5% = 0,05 n = 6 лет FVA = 19 000 000 руб.

Размер ежегодных платежей:

(руб.)

Ответ: размер ежегодных платежей равен 2 793 331,894 руб.

Решение: R = 19 000 руб. N = 2 года I = 5% = 0,05

Величина будущего фонда:

(руб.)

Ответ: величина будущего фонда равна 38 950 руб.

Годовых.

Решение: R = 1 800 руб. j = 48% = 0,48 m = 12 n = 1 год

Авансовая приведённая сумма аренды:

(руб.)

Ответ: равноценный платёж, взимаемый за год вперёд, равен 17 568,858 руб.

Полугодовых купона доходностью 20% годовых каждый. Рассчитать цену её первоначального размещения, приняв ставку сравнения 16%.

Решение: N = 2 года N = 1 000 руб. M = 2 J = 16% = 0,16 Q = 20%

Цена первоначального размещения облигации:

1 066,243 (руб.)

Ответ: цена первоначального размещения облигации равна 1 066,243 руб.

Решение: дней Т = 360 дней

1) доходность по схеме простых процентов:

2) доходность по схеме сложных процентов:

Ответ:

– доходность по схеме простых процентов равна 180%;

– доходность по схеме сложных процентов равна 342,1%.

Решение: I = 5% = 0,05 N = 5 лет PVA = 1 500 000 руб.

1) амортизация займа, погашаемого равными суммами

Сумма погашения основного долга:

(руб.)

Сумма срочной уплаты:

Остаток долга на начало периода:

Таблица –

2) амортизация займа, погашаемого равными срочными уплатами

Срочный платёж:

(руб.);

Сумма процентов:

Погасительный платёж:

Остаток долга на начало периода:

Таблица –

Решение.

Способ 1.

K’ = K I = 4000 44=4044,

 где K – капитал или заем, за использование которого заемщик выплачивает определенный процент;

I – процентный платеж или доход, получаемый кредитором от заемщика за пользование денежной ссудой;

P – процентная ставка, показывающая сколько д. е. должен заплатить заемщик за пользование 100 ед. капитала в определенном периоде времени (за год);

D – время, выраженное в днях.

360 – число дней в году.

Способ 2.

Время t = 80/360 = 2/9.

K’ = K K×i×t = 4000(1 0.05×2/9) = 4044,

Где i – процентная ставка, выраженная в долях единицы,

T – время, выраженное в годах.

Решение

2×K = I.

2×K = K×9×g/100,

G = 2×100/9 = 22.22

Постнумерандо по 5000 д. е. при 8% годовых, если капитализация осуществляется каждые полгода.

Решение:

При ежегодной капитализации: C0 = a×IVpn = 5000×IV8 = 5000×6.71=33550

Решение

Таблица – План погашения займа (амортизационный план)

Пояснения к таблице

Аннуитет вычисляем по формуле: a = K×Vpn = 20000×V2 = 20000×0.1113 = 2226.53 д. е.

Чтобы определить выплату задолженности b1, вычисляем величину процентного платежа I:

I1 = K1×p/100 = 20000×2/100 = 400 д. е.

Выплата задолженности представляет собой разницу между аннуитетом и процентным платежом:

B1 = a – I1 = 2226.53 – 400 = 1826.53 д. е.

Таким образом, после первого года долг сократится на 1826.53 д. е. Остаток долга равен:

K2 = 20000 – 1826.53 = 18173.47 д. е.

Вычислим процентный платеж на остаток долга:

I2 = 18173.47×2/100 = 363.47 д. е.

Вторая выплата составит:

B2 = a – I2 = 2226.53 – 363.47 = 1863.06 д. е.

Долг уменьшится на величину 1863.06, остаток долга составит:

K3 = 18173.47 – 1863.06 = 16310.41 д. е.

Далее

I3 = 16310.41×2/100 = 326.21 д. е.

Третья выплата задолженности составит:

B3 = a – I3 = 2226.53 – 326.21 = 1900.32 д. е.