- А что если первоначальная сумма не нулевая
- History 3 февраля 2022 г.
- Будущая стоимость платежей
- Будущая стоимость платежей и суммы вклада
- Будущая стоимость суммы вклада
- Годовые проценты
- Ежедневная капитализация
- Зачем нужно считать накопления?
- Как использовать сложные проценты в инвестировании
- Как посчитать сложный процент в excel с пополнением и капитализацией
- Какие бывают проценты по вкладам в банке
- Какие вклады облагаются налогом
- Калькулятор доходности вкладов
- Корректировка в программе излишне признанного дохода за апрель, май, июнь 2022г.
- Начисляем проценты за апрель, май, июнь месяц 2022г.
- Ограничения и область применимости формул
- Округление в финансовых формулах
- Определяем срок долга
- Определяем сумму начисленных процентов
- Примеры решения задач по сложным процентам
- Проценты на остаток денежных средств 1с – учет без забот
- Расчет сложных процентов
- Сложный процент: как использовать секрет миллиардеров? формулы расчёта, калькулятор в excel
- Учет (дисконтирование) по сложным процентам
- Формула простого процента
- Формула расчета сложных процентов с пополнением
- Формула сложного процента
А что если первоначальная сумма не нулевая
Если у вас стоит немного другая задача — сколько нужно пополнять текущий вклад, если сумма вклада равна 100 тыс. и требуется накопить 1.5 млн. рублей за 10 лет при ставке 10% годовых. В таком случае, нашу исходную формулу нужно немного модифицировать, добавив в нее часть, связанную с первоначальным взносом
В этой формуле А — первоначальная сумма вклада, а вторая часть слагаемого — это формула сложных процентов(процент с капитализацией)
Уже из этой форумлы нужно выразить PMT — ежемесячный взнос. Но это уже дело математики вам нужно постараться самому(ой). Если не получится, пишите в комментариях, я ее приведу.
Данные формулы являются универсальными и подходят для расчета возможного срока депозита(когда вы знаете, сколько будете пополнять и какую сумму хотите достигнуть) В данном случае вам будет интересен срок, нужно просто выразить переменную n.
History 3 февраля 2022 г.
Рассмотрим Сложный процент (Compound Interest) – начисление процентов как на основную сумму долга, так и на начисленные ранее проценты.
Немного теории
Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.
Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по простым и сложным процентам.
При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования простых процентов изменяется в каждом периоде начисления.
В файле примера приведен график для сравнения наращенной суммы с использованием простых и сложных процентов.
Будущая стоимость платежей
В этом примере мы предположим, что открыли накопительный счет для своего ребенка, чтобы к окончанию школы насобирать ему сумму, необходимую для платного обучения в университете. Начиная со следующего месяца, вы будете ежемесячно откладывать 50 долларов на этот счет под 3% годовых.
Годовую процентную ставку 3% мы преобразуем в месячную; 18 лет также преобразуем в месяцы. Приведенная стоимость отсутствует, так как вы только что открыли счет. Аргумент Тип равен нулю, так как вносить суммы вы начинаете со следующего месяца.
Будущая стоимость платежей и суммы вклада
Также можно вычислить будущую стоимость и уже существующего вклада, на который периодически будут добавляться (или сниматься) деньги. В предлагаемом примере мы собираемся вносить ежемесячные платежи в сумме 900 долларов по закладной на сумму 150 тысяч долларов.
Платежи вносятся ежемесячно, поэтому все остальные аргументы мы соотносим с месяцами — количество лет умножается, а процентная ставка делится на 12. Текущий баланс показан как приход денег, хотя на самом деле они не поступают в настоящий момент — это движение было, когда мы изначально покупали дом.
Лучше представить себе данную задачу следующим образом. Некто одолжил вам 150 тысяч долларов, чтобы выкупить закладную на дом, хотя на самом деле этого не произошло. Вычисленное значение — 137435,10 — это сумма выходного потока по истечении пяти лет.
Будущая стоимость суммы вклада
В следующем примере вычисляется будущая стоимость суммы денег, которая не будет пополняться, и с нее не будут сниматься деньги. Предположим, что вы открыли пенсионный счет, внесли на него 20 тысяч долларов и планируете через 15 лет выйти на пенсию (рис. 2): =БС(,08;15;0;-20000;0).
В данном примере предполагается, что пенсионный вклад гарантирует получение 8% годовых. Значение -20000 представляет двадцать тысяч долларов, уходящих от вас в банк. В результате мы получаем 63443,38 долларов — эту сумму вы получите через 15 лет при выходе на пенсию.
Годовые проценты
Для сравнения условий вкладов используется годовая доходность. Можно вычислить, например, квартальную ставку, но удобнее сравнивать именно годовую.
Банки в своих предложениях указывают номинальную ставку годовых, которая не учитывает капитализацию, если она есть. В этом случае полезно рассчитать эффективную процентную ставку.
Эффективная процентная ставка позволяет сравнивать вклады с разными условиями: например, по одному вкладу проценты начисляются раз в месяц и капитализируются, а по другому выплачиваются в конце срока. Эффективная ставка позволяет привести эти два вклада к общему знаменателю и понять, какой из них выгоднее.
Ежедневная капитализация
Рассчитать доход за каждый день действия вклада поможет следующая формула:
где
Дв — сумма на конец срока, включая сумму открытия и начисленный процент, Р — первоначальный размер депозита,N — годовая процентная ставка, разделенная на 100,К — количество дней в году — 365 или 366,Т — срок вложения в днях.
Если клиент внес 350 000 руб. под 4,7% на 9 месяцев или 273 дня, в конце срока он получит:
Возвести число в большую степень можно на инженерном калькуляторе, где есть функция x^y, воспользоваться онлайн-сервисами или калькуляторами на сайтах банков.
Зная Дв, легко вычислить сумму процентов по вкладу за весь период:
Зачем нужно считать накопления?
Допустим мы хотим купить жилье за 1 500 000 рублей. Покупку хотим сделать через 10 лет. Возникает вопрос, какую сумму необходимо класть в банк каждый год, чтобы через 10 лет получить 1 млн. 500 тыс? По идее стоит открыть вклад и копить. Ставка по депозиту в банке — 10% годовых.
Речь идет о вкладе с капитализацией, капитализация каждый год, под 10 процентов в год. Вопрос, какую сумму нужно откладывать с зарплаты? Нужно понимать, является ли эта сумма большой и хватит ли оставшихся денег на жизнь? Зная простую формулу, описанную ниже, можно без труда все посчитать.
Как использовать сложные проценты в инвестировании
Как вы уже знаете, получаемая от инвестиций прибыль — это важный инструмент, который на большой дистанции может во много раз увеличить доходность ваших вложений. Метод повторного вложения прибыли называется реинвестированием.
Безусловно, использовать эффект сложного процента должен каждый инвестор, однако на практике это не так просто как кажется. Существует несколько проблем, которые мешают теоретически супервыгодное реинвестирование реализовать в реальных условиях. Например, вряд ли вы слышали о людях, ставших миллиардерами через банковские депозиты.
Дело в том, что деньги постоянно обесцениваются из-за инфляции — постоянного повышения цен на товары и услуги. На самом деле ставка банковских депозитов обычно примерно равна инфляции или даже ниже, поэтому реальная доходность вкладов не впечатляет:
Даже если оставить удачный бескризисный отрезок 2022-2020 годов, доходность банковского вклада с учётом инфляции была в районе 1-2% годовых в рублях. Не говоря уже о доходности в долларах, которая после 2022 года, очевидно, находится в еще большем минусе.
Кроме инфляции сильно повлиять на итоговую доходность инвестиций могут разнообразные комиссии. Если их размер зависит от суммы инвестиций, убытки накапливаются по правилу сложных процентов, но уже с негативным эффектом. Это значит, что за несколько десятков лет инвестор может потерять сотни или даже тысячи процентов прибыли.
Такое часто встречается при инвестициях в ETF, где комиссия за управление достигает несколько процентов от депозита в год. Один из самых старых ETF под тикером SPY (инвестиционная стратегия — следование за индексом S&P 500) работает с 1993 года и берет с клиентов 0.
09% в год — немного, по сравнению с другими биржевыми фондами. Эта ставка со временем может меняться, но давайте для эксперимента представим что она всегда была такой — и сравним, как будет отличаться доходность инвестиций при комиссиях от 0 до 2% в год:
Как видите, даже из-за несчастных 0.09% инвестор на дистанции 27 лет потерял 25% прибыли. А вроде бы небольшая комиссия в 2% годовых срезает доходность почти в 3 раза — с 723% до 270%, и это еще не учтена инфляция. По причине скрытых комиссий высокая доходность активов на самом деле может оказаться в разы ниже, поэтому перед принятием решения об инвестировании важно учитывать даже мизерные расходы.
Куда же стоит инвестировать, чтобы использовать эффект сложного процента на максимум и минимизировать влияние инфляции и комиссий? Я бы выделил такие инструменты:
Конечно, в любых инвестициях можно использовать правило сложных процентов, но не везде это рекомендуется делать. Чем выше риски вложений, тем выгоднее просто выводить прибыль, поскольку при неудачных раскладах депозит может быть потерян.
Как посчитать сложный процент в excel с пополнением и капитализацией
Функция БС в Excel…
Очень полезная формула для людей, имеющих сбережения в банке, или располагающие другими инвестиционными формами вложение денежных средств. Думаю, увидев первый раз описание этой формулы в самом Microsoft Excel понять её предназначение довольно сложно.
Начинаем разбираться, как ей пользоваться. Итак, заходим в Microsoft Excel вводим формулу =БС и далее рекомендуется нажать Аргументы функции.
Вот теперь начнём заполнять поля исходя из нашего примера.
Первое поле Ставка. В нашем примере сюда вписываем 12%/365, 12 процентов – это годовая ставка, а 365 количество дней, периодов по которым считается процент. Если процент высчитывается (не путать с выплатами) один раз в месяц, то делить придётся на 12 (месяцев).
Второе поле Кпер. Это количество периодов, отображающих нахождение в банке (для нашего опять же случая). Мы положили на год или 365 дней, соответственно вводим 365.
Третье поле Плт. Выплата, которую мы будем снимать каждый период. Но мы не будем ничего снимать, поэтому оставляем незатронутой или ставим 0.
Чётвертое поле Пс. Приведенная стоимость – та сумма, которую мы изначально инвестируем. Важный момент, т.к. мы её отдаём и для нашего кармана это временный минус, то и вводить нужно число отрицательное.
Пятое поле Тип. Заполнение этого поля имеет значение, в случае заполнения поля Плт. Если Плт не трогали, то и Тип можно оставить не тронутым. Есть только два варианта заполнения поля 0 или 1. Ноль вводиться при выплате в начале периода, а единица при выплате в конце периода.
Источник
Какие бывают проценты по вкладам в банке
Проценты бывают двух видов: простые и сложные.
Простые — те, что начисляются в конце срока вклада. Например, вы положили 100 000 Р на год под 5% годовых. Через год на вашем счете будет 105 000 Р.
Сложные. Несмотря на название, принцип их прост — они начисляются в течение срока вклада через равные интервалы. Например, ежемесячно или ежеквартально. Проценты начисляются на первоначальную сумму и на проценты от предыдущих периодов — вы получаете проценты на проценты. Это называется капитализацией.
В случае с ежемесячным начислением и вкладом на год вы как будто открываете вклад 12 раз подряд на 1 месяц, причем сумма вклада каждый раз увеличивается на сумму выплаченных за предыдущий месяц процентов.
Рассмотрим вклад на 100 000 Р под 4,8% годовых с ежемесячной капитализацией. Процент доходности в месяц составляет: 4,8% / 12 месяцев = 0,4%. Значит, на вкладе по истечении первого месяца будет 100 400 Р.
Во втором месяце эти 0,4% начислятся не на изначальные 100 000 Р, а на сумму вместе с процентами — 100 400 Р. И так далее каждый месяц. При закрытии вклада через год на нем будет 104 907,02 Р — доход за год составит 4907,02 Р. Это соответствует годовой доходности чуть более 4,9% годовых.
Какие вклады облагаются налогом
Например, у вас два вклада по 600 000 Р со ставкой 4,8% годовых. По каждому вы получите доход в размере 28 800 Р. В сумме это будет 57 600 Р. Значит, налог вы заплатите с 57 600 − 42 500 = 15 100 Р. Величина налога составит 15 100 × 13% = 1963 Р.
В 2022 году безналоговый лимит может измениться, так как он зависит от ключевой ставки Центробанка России на 1 января.
Калькулятор доходности вкладов
Если примеры расчетов кажутся сложными, посчитайте эффективную процентную ставку по вкладу с помощью нашей эксельки:
Корректировка в программе излишне признанного дохода за апрель, май, июнь 2022г.
Теперь нам необходимо в программе 1С:Бухгалтерия 8.3 провести корректировки по начисленным процентам за апрель, май, июнь 2022 г. в связи с излишним начислением процентов по размещению депозита.
Для этого заходим Операции/Операции, введенные вручную/Создать – вид документа выбираем «Сторно документа».
Заполняем открывшуюся карточку документа:
- «От» – указываем дату учета операции 03.07.2022;
- «Сторнируемый документ» – нажимаем на три точки;
- В открывшемся окне выбираем «Операция»;
- Нам необходимо выбрать документ для сторнирования: выбираем первый документ «Операции, введенные вручную/Начисление процентов за апрель 2022;
- Все остальные поля и табличная часть заполнятся автоматически;
- Записать и закрыть.
Корректировку необходимо делать отдельными документами на каждую операцию по начисленным процентам на депозит за апрель, май и июнь 2022.
Начисляем проценты за апрель, май, июнь месяц 2022г.
Нам необходимо отразить в программе операцию по начислению процентов за апрель месяц. Заходим Операции/Операции, введенные вручную/Создать/Вид документа выбираем – «Операция»
Заполняем открывшуюся карточку документа:
- «От» – указываем дату учета операции 01.05.2022;
- «Содержание» – прописываем содержание нашей операции;
- «Сумма операции» – указываем сумму процента начисления за апрель 2022 .Рассчитывается по формуле 28 493,15 руб.= ((5 000 000* 8%)/365)*26 (где 8% ставка по договору, 365 количество дней в году, 26 количество дней за апрель).
Нам необходимо указать проводки «Проводки по начислению банковских процентов» в табличной части документа.
Нажимаем «Добавить» в табличной части.
Заполняем табличную часть документа:
- «Дебет» – выбираем субсчет 76.09 «Прочие расчеты с разными дебиторами и кредиторами»;
- «Субконто 2Дт» – из справочника «Контрагенты», выбираем наш «ПАО «Сбербанк»;
- «Субконто 3Дт» – выбираем депозитный договор «55»;
- «Субконто 4Дт» – указываем документ расчетов с контрагентами. В нашем примере это «Списание с расчетного счета 0000-000001 от 05.04.2022»;
- «Кредит» – выбираем счет 91.01 «Прочие доходы»;
- «Субконто Кт2» – статья ДДС «Проценты к получению (уплате);
- Записать и закрыть.
Далее так же начисляем проценты в программе, отдельным документом за май, которые составят: 33 972,60 руб = ((5 000 000* 8%)/365)*31 (где 8% ставка по договору, 365 количество дней в году, 31 количество дней за май).
И за июнь: 32 876,71руб =((5 000 000* 8%)/365)*31 (где 8% ставка по договору, 365 количество дней в году, 30 количество дней за июнь).
Ограничения и область применимости формул
Однако стоит учитывать, что данные расчеты подходят для студентов при решении задач, но не работают при точных банковских расчетах. Здесь вам может помочь депозитный калькулятор, поскольку он учитывает даты, выходные, ставку рефинансирования ЦБ. Т.е. данная формула не учитывает налог по депозиту. Налог же зависит от ставки рефинансирования ЦБ и валюты вклада.
Т.е. данный расчет будет приблизителен в любом случае. Тут нет учета числа дней в году также. Однако, если даны эталонные условия, как это делается в студенческих задачах, данную формулу можно с успехом применять в их решении. Данная формула позволяет получить ответ на следующие вопросы:
Формула может быть успешно использована для прогнозирования дохода по вашим средствам в банке — будь то вклад или доходная карта
Источник
Округление в финансовых формулах
При использовании финансовых формул проблема округления значений ощущается особенно остро. Excel предлагает несколько функций для выполнения этой задачи: ОКРУГЛ, ОКРУГЛВНИЗ И ОКРУГЛВВЕРХ. Чтобы предотвратить накопительные ошибки, округляйте только конечный получаемый результат.
Другими словами, избегайте округления промежуточных данных. Обычно результаты финансовых расчетов отображаются в виде чисел с двумя десятичными разрядами или вообще без таковых. В промежуточных расчетах это предполагает получение результатов с точностью до цента или доллара.
В отдельных случаях вычисления базируются на приблизительных данных или данных, полученных в результате эмпирического анализа или подбора параметров. Поэтому уже давно обычной практикой стало применение округленных значений (чтобы не утруждать себя вводом длинных значений).
Однако вы знаете, что арендная плата может изменяться (скажем, в диапазоне от 42 до 45 долларов). В результате конечная сумма аренды будет колебаться в небольших пределах. Чтобы избежать излишней неточности, конечную сумму можно округлить до ближайших ста или даже тысячи долларов.
Определяем срок долга
Рассмотрим задачу: Клиент банка положил на депозит некую сумму с ежегодным начислением сложных процентов по ставке 12 % годовых. Через какой срок сумма вклада удвоится? Логарифмируя обе части уравнения S = Р*(1 i)^n, решим его относительно неизвестного параметра n.
В файле примера приведено решение, ответ 6,12 лет.
Определяем сумму начисленных процентов
Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. на 5 лет с ежегодным начислением сложных процентов по ставке 12 % годовых. Определить сумму начисленных процентов.
Сумма начисленных процентов I равна разности между величиной наращенной суммы S и начальной суммой Р. Используя формулу для определения наращенной суммы S = Р*(1 i )^n, получим: I = S – P= Р*(1 i)^n – Р=P*((1 i)^n –1)=150000*((1 12%)^5-1) Результат: 114 351,25р. Для сравнения: начисление по простой ставке даст результат 90 000р. (см. файл примера ).
Примеры решения задач по сложным процентам
В этом разделе мы пройдемся по некоторым типичным задачам на сложные проценты. Также вы найдете шаблоны расчётов в Excel, в которых можно поменять вводные данные и получить нужное вам решение.
Задача №1. Рассчитать прибыль по вкладу на 5 лет под 10% годовых, начальная сумма вложений 100000 рублей (с капитализацией).
Находим конечную сумму вклада по формуле сложных процентов:
Результат: инвестор через 5 лет получит 61051 рублей прибыли.
Задача №2. Рассчитать прибыль по вкладу на 10 лет под 10% годовых с капитализацией. Начальная сумма вложений 50000 рублей, дополнительно каждый год начиная с первого счёт пополняется на 10000 рублей.
Сначала находим конечную сумму по формуле сложного процента с регулярными пополнениями:
Учитывая, сколько инвестировано за 10 лет (50000 сразу и еще 9 раз по 10000), вычисляем прибыль:
Результат: инвестор через 10 лет получит 139061 рубль прибыли, инвестировав 140000 рублей.
Задача №3. Рассчитать, сколько времени понадобится инвестору, чтобы увеличить капитал с 500000 до 1000000 рублей. Средняя доходность портфеля — 12% годовых, прибыль реинвестируется.
У нас есть все необходимые данные, используем одну из производных формул сложных процентов:
Решение: инвестору понадобится чуть больше 6 лет.
Задача №4. Посчитать среднюю процентную ставку, которая позволит превратить 100000 рублей в 500000 рублей за 10 лет путём инвестирования. Прибыль реинвестируется.
Используем одну из производных формул сложных процентов:
Решение: инвестору нужно вложить деньги под 17.5% годовых (довольно сложно на практике, кстати).
Думаю, этого достаточно. Если ваша задача не похожа ни на одну из предыдущих, возможно вам поможет информация из следующего раздела статьи.
Проценты на остаток денежных средств 1с – учет без забот
- Опубликовано 04.11.2022 15:46
- Автор: Administrator
- Просмотров: 42514
Сегодня банки предлагают немало бонусов, чтобы замотивировать клиентов на открытие расчетного счета именно у них. Одним из таких бонусов является начисление процентов на остаток денежных средств. Такое преимущество позволяет “работать” временно свободным деньгам, не допуская их замораживания и изъятия из оборота. В отличие от депозита и банковских вкладов, расчетные счета с начислением процентов позволяют организации в любой момент воспользоваться денежными средствами.
Большую прибыль данные начисления принести вряд ли смогут, но покрыть стоимость некоторых услуг банка или компенсировать уровень инфляции вполне способны. Понятно, что ни одна организация не откажется от получения такого рода “пассивного дохода”, но у бухгалтеров, сталкивающихся с данной операцией впервые, возникает немало вопросов. В статье мы подробно разберем данную операцию на примере программы 1С: Бухгалтерия предприятия.
Поступление процентов на расчетный счет организации
Обычно банки перечисляют проценты или последним числом месяца, или в первых числах следующего месяца. Поступление денежных средств на расчетный счет организации отражается в банковской выписке документом “Поступление на расчетный счет” (“Банк и касса” – “Банковские выписки”).
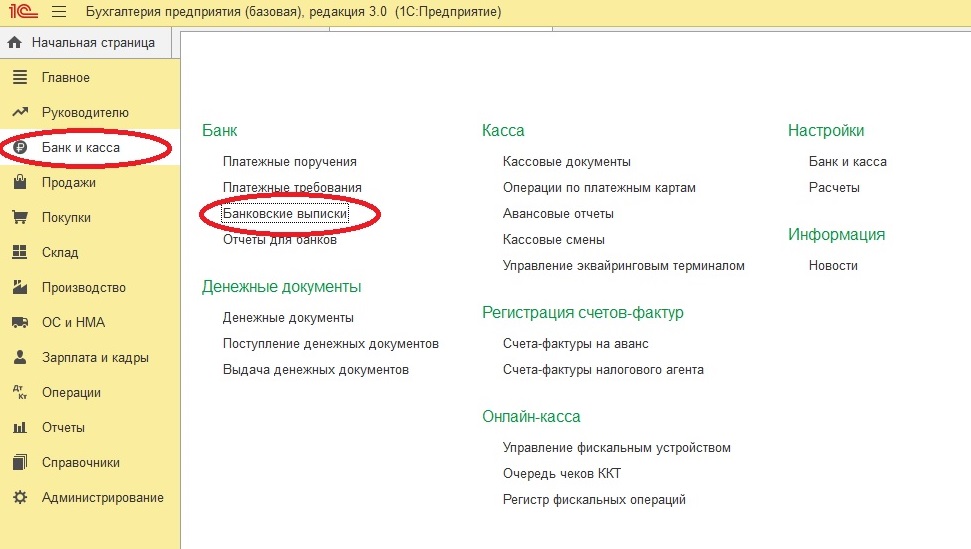
В бухгалтерском учете поступление на расчетный счет процентов, начисленных на остаток денежных средств, отражается проводкой:
Дт 51″Расчетные счета” Кт 76.05 “Расчеты с разными дебиторами и кредиторами” – получены проценты на остаток по расчетному счету.
В данном документе важно правильно указать вид операции: «Прочие поступления».

Начисление процентов
Начисление процентов производится документом “Операция” (“Операции” – “Операции, введенные вручную” – кнопка “Создать” – вид документа “Операция”).
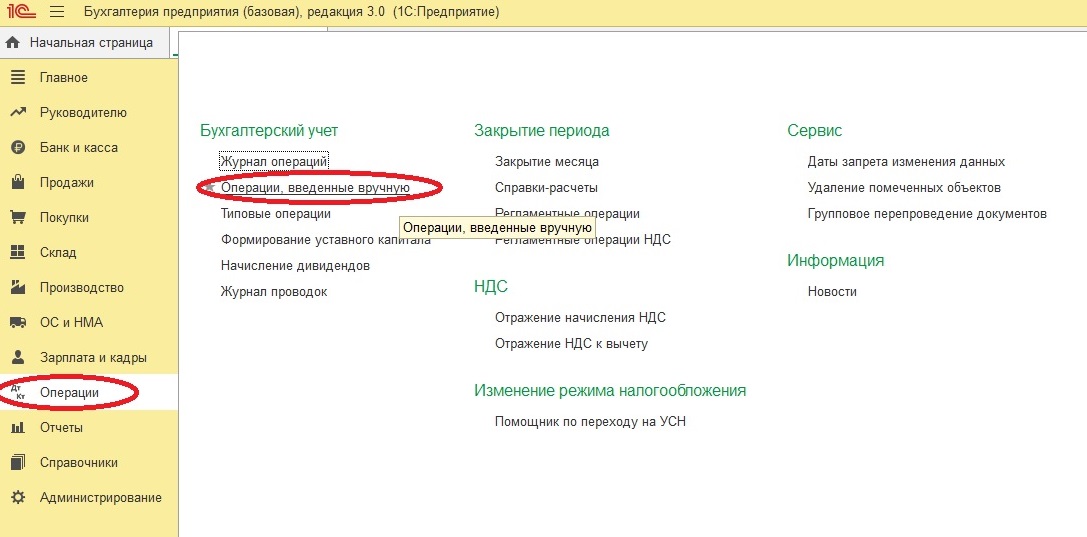
Далее необходимо ввести следующую проводку:
Дт 76.05 «Расчеты с разными дебиторами и кредиторами» Кт 91.01 «Прочие доходы» – Начислены проценты, на остаток по расчетному счету.
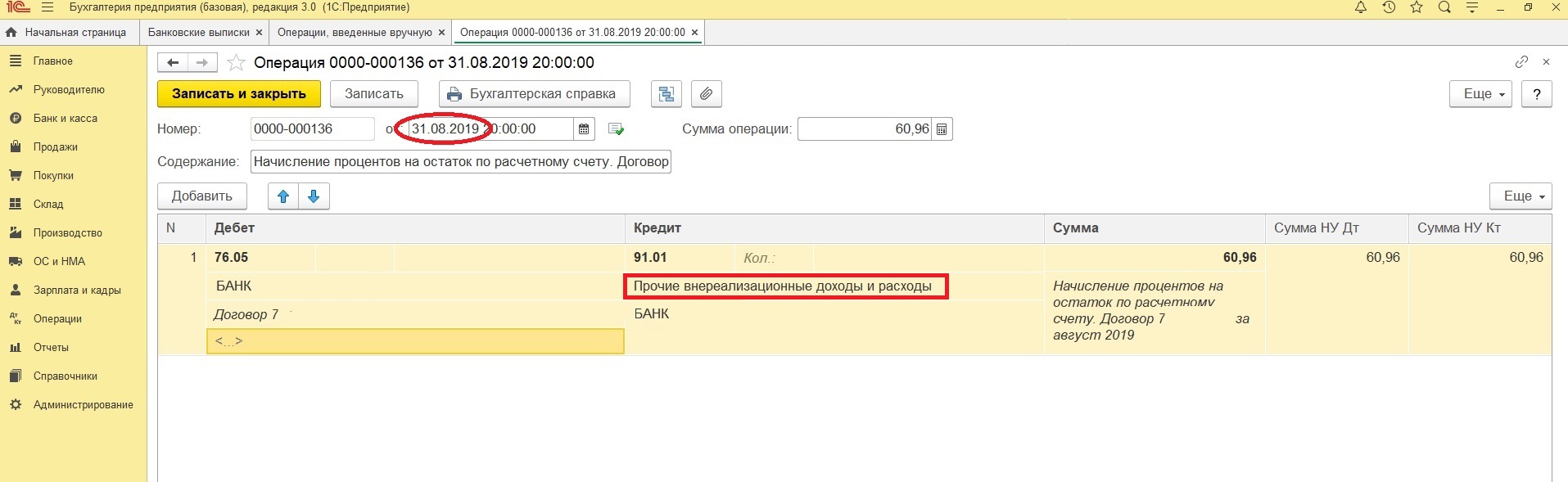
В целях налогового учета доходы в виде процентов банка признаются внереализационными (п.6 ст. 250 НК РФ).
Важно помнить: начисление процентов должно производиться последним днем месяца, вне зависимости от того, когда банк фактически перечислил денежные средства на расчетный счет организации. (п.1 ст. 271 НК РФ)
Такие доходы не включаются в книгу продаж, так как не подлежат обложению НДС (ст. 149 НК РФ).
Проверка отражения в программе
Формируем отчет «Анализ счета» (76.05) или оборотно-сальдовую ведомость по счету 76.05
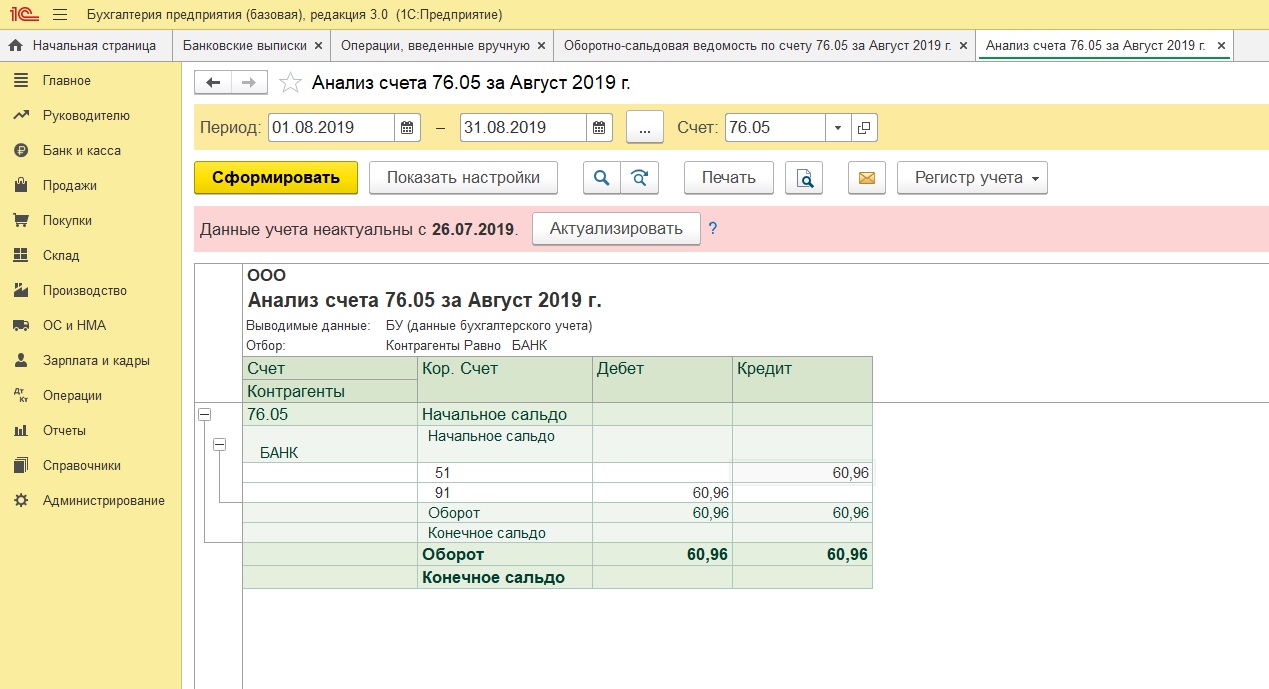
Сумма процентов начислена и перечислена на расчетный счет организации.
Автор статьи: Марина Аленина

Понравилась статья? Подпишитесь на рассылку новых материалов

Расчет сложных процентов
Вот некоторые банковские опции по депозитам.
Вклады с капитализацией. Как мы уже рассмотрели, вклады с начислением процентов поэтапно внутри срока называются вкладами с капитализацией. Периодичность капитализации может быть разная, обычно — раз в месяц, но бывает ежедневная или раз в квартал.
Если банк капитализирует проценты по вкладу — начисляет и добавляет их к сумме депозита, при равных номинальных ставках такой вариант будет выгоднее, чем при начислении процентов в конце срока.
Рассмотрим варианты начисления процентов — от ежедневного до одного раза в квартал. Во всех случаях будем считать, что вы открыли депозит на 100 000 Р под 4,8% годовых на 1 год.
Ежедневная капитализация. Каждый день банк начисляет проценты и добавляет их к сумме вклада.
Упрощенный расчет будет выглядеть так.
Проценты за первый день: 100 000 × 4,8% / 365 = 13,15 Р — эту сумму банк добавит к сумме вклада по истечении первого дня.
За второй день: (100 000 13,15) × 4,8% / 365 = 13,15 Р.
За третий день: (100 000 13,15 13,15) × 4,8% / 365 = 13,16 Р.
С каждым днем сумма, на которую начисляются проценты, будет расти. Соответственно, и процентов каждый месяц будет начисляться больше.
Через год у вас на счете будет 104 916,73 Р. Эффективная ставка составит 4,92% годовых.
Ежемесячная капитализация. Каждый месяц банк будет начислять проценты и добавлять их к сумме вклада.
Упрощенный расчет будет выглядеть так.
Через год у вас на счете будет 104 907,02 Р. Эффективная ставка составит 4,91%.
Ежеквартальная капитализация. Проценты начисляются раз в три месяца. Упрощенный расчет будет выглядеть так.
Через год у вас на счете будет 104 887,09 Р. Эффективная ставка составит 4,89%.
Вклады с пополнением. Если по условиям договора вклад можно пополнять — вносить дополнительные средства, — с момента внесения процент начисляется на общую сумму.
Пример: вы открыли счет на 100 000 Р под 4,8% годовых на 1 год с возможностью пополнения, а через полгода внесли еще 50 000 Р. При годовой ставке 4,8% за полгода банк начислит 2,4% от суммы депозита. Рассчитаем процентные начисления за каждые полгода отдельно.
Без учета капитализации сумма процентных начислений составит 6 000 Р. Вкладчик в этом случае получает фиксированный процент от вложенных денег, поэтому эффективная ставка здесь не меняется — 4,8% годовых.
Если вклад с капитализацией, для вычисления эффективной процентной ставки можно отдельно рассчитать периоды до и после пополнения — как будто это два разных депозита. Эффективная ставка у вкладов будет другой из-за изменения длительности.
где:
- СО — это средний остаток по счету в течение всего срока, как если бы вы клали деньги на беспроцентный депозит;
- Д — общая длительность вклада в годах.
Это и есть смысл эффективной ставки: она показывает, под какой процент нужно вложить средний остаток по счету, чтобы получить те же проценты за тот же срок.
Вклады с частичным снятием. Иногда по условиям договора банк разрешает снимать со счета часть средств, которые лежат на депозите. При этом проценты с момента открытия депозита до момента снятия не теряются.
Пример: вы открыли депозит на 100 000 Р под 4,8% годовых на 1 год с возможностью частичного снятия, а через полгода сняли 50 000 Р. При годовой ставке 4,8% за полгода банк начислит 2,4% от суммы вклада. Рассчитаем проценты за каждые полгода отдельно.
Без капитализации сумма процентов составит 3600 Р. Эффективная процентная ставка без ежемесячной капитализации — те же 4,8%.
Расчет эффективной ставки с капитализацией можно произвести аналогично вкладу с пополнением.
Сложный процент: как использовать секрет миллиардеров? формулы расчёта, калькулятор в excel
Привет всем читателям Блога Вебинвестора! Думаю, каждый из вас сталкивался с начислением процентов на денежную сумму — по депозиту, по кредиту, расчётом доходности инвестиций и так далее. Так вот, если повторить эту процедуру много раз, вложения начинают расти всё быстрее и быстрее благодаря эффекту сложного процента!
Эта статья входит в бесплатное обучение инвестициям с нуля на Блоге Вебинвестора. В комментариях к статье вы можете оставлять любые вопросы по теме и я постараюсь подробно на них ответить.
Спасибо за внимание, продолжаем!
Учет (дисконтирование) по сложным процентам
Дисконтирование основывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Рассмотрим 2 вида учета: математический и банковский.
Решение. P = 2000000/(1 15% )^7 Значение текущей стоимости будет меньше, т.к. открыв сегодня вклад на сумму Р с ежегодной капитализацией по ставке 15% мы получим через 7 лет сумму 2 млн. руб.
При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.
Источник
Формула простого процента
По этой формуле мы можем рассчитать конечную сумму вклада без капитализации полученной прибыли. Для этого нужно знать начальную сумму вклада, процентную ставку за 1 период инвестирования и временной интервал. Если конечная сумма задана сразу и нужно найти другую неизвестную переменную, используйте производные формулы простого процента:
Формула расчета сложных процентов с пополнением
В нашем случае имеем следующие данные
| Условия по вкладу | |
|---|---|
| Планируемая сумма FV | 1 млн. 500 тыс |
| Ставка i | 10% |
| Срок n | 10 лет, начисление ежегодно |
| Капитализация процентов | Да |
Мы можем выразить из формулы нужный нам ежегодный взнос 
Подставив в эту формулу наши значения получим

94118,09232 — именно эту сумму мы должны вкладывать каждый год, чтобы получить через 10 лет 1.5 млн. рублей.
Но на самом деле этот расчет приблизительный. Точный расчет можно получить с помощью калькулятора вкладов

Выше приведен расчет депозита на 10 лет с 2 июля 2009. Ежегодное пополнение 94118,09232 Сумма получилась примерно такой(разница 35 рублей не существенна)
Формула сложного процента
По этой формуле мы можем посчитать конечную сумму вклада с учётом капитализации полученной прибыли, зная начальный депозит, процентную ставку и нужный временной интервал. Для решения задач также можно использовать производные формулы сложного процента:
На практике часто дело не заканчивается первоначальным депозитом — многие пользуются регулярными пополнениями, например делают регулярные инвестиции из зарплаты. Для этих случаев формула сложного процента становится длиннее:
где D — сумма регулярных пополнений банковского депозита. Обратите внимание, степень N-1 означает, что доливки начинаются со второго инвестиционного периода (если сумма дополнительных инвестиций вносится сразу, то N-1 меняется на N).
Ну что, удачи на экзаменах всем читающим меня студентам 🙂 Для закрепления далее мы разберем несколько примеров задач на сложные проценты.





