Операции с потоками денежных средств и концепция npv
Ключевой концепцией, позволяющей сопоставлять выгоды между сегодняшними оттоками денежных средств и будущими денежными выгодами, является концепция временной стоимости денег (time value of money). Главный посыл концепции: «деньги сегодня не равны деньгам завтра», основной причиной которого является упускаемая возможность инвестирования (зарабатывания), а также инфляция (рис. 1.6). Ии-

Рис. 1.6.Три причины различия равнономинальных денежных потоков разных моментов времени
вестору (собственнику и кредитору) следует уметь правильно сопоставлять затраты и ожидаемые выгоды, которые могут быть «размазаны» во времени.
В связи с этим в инвестиционной аналитике особое внимание уделяется вопросам расчета будущей и текущей стоимости денежных потоков, соответствующей ставки процента, а также ожидаемому периоду возврата инвестированных сумм. Введем следующие обозначения для четырех ключевых переменных концепции временной стоимости денег (рис. 1.7):
- 1) PV (present value) — текущая (сегодняшняя) стоимость ожидаемых будущих выгод. В конкурентной рыночной среде это справедливая оценка активов на рынке;
- 2) FV (future value) — будущая стоимость;
- 3) г — рыночная процентная ставка, отражающая возможности инвестирования, а также стоимость денег;
- 4) п — инвестиционный период (число лет).
Денежные выгоды могут носить разовый характер или же иметь вид потока платежей. В инвестиционной аналитике важно знать, с какой периодичностью и в каком номинальном размере имеют место денежные поступления или оттоки.
Аннуитетный поток — ряд денежных потоков, которые равны по номиналу и поступают через равные промежутки времени. Различают бессрочные аннуитеты (их период жизни — бесконечность) и срочные (например, 2, 5 или 10 лет).
Специальные таблицы, формулы и ряд простых правил позволяют инвестору найти искомые величины (FV, PV, г или п) при знании трех других переменных для сопоставления разных вариантов инвестирования или финансирования по привлекательности.
Будущая стоимость может быть рассчитана исходя из простых или сложных процентов. Для одногодичного инвестиционного периода формула едина:

По правилу простых процентов будущая стоимость наращивается ежегодными процентными выгодами, которые не капитализируются:


Рис. 1.7.Ключевые переменные концепции временной стоимости денег
По заявленной ставке начисляются проценты только на первоначальную сумму взноса.
По правилу сложных процентов будущая стоимость единичного вложения рассчитывается по формуле

где (1 г) — множитель наращения; п — число лет наращения.
Сложные проценты начисляются не только на первоначальную сумму, но и на сумму процентов, которые накопились за истекший период. В этом случае процентный доход не изымается, а остается на счете и прибавляется к величине первоначального взноса. Такой расчет предполагает, что инвестор не исключает из проекта (например, из банковского депозита) ни проценты, ни сумму первоначального взноса, вкладывает деньги на несколько лет под фиксированный процент, сумма накопленных процентов не изымается (не переводится на текущий счет), а капитализируется, т.е. на нее начисляются проценты.
Пример 1.1. Рассмотрим пример размещения инвестором 1000 руб. на банковском депозите под 9% годовых сроком на один год и пять лет. Через год инвестор на вложенный вклад получит 90 руб. (1000 • 0,09). Денежная выгода инвестора через год будет равна сумме вклада плюс накопленные проценты: 1000 90 = 1090 руб. Следовательно, будущая стоимость сегодняшней 1000 руб. равна 1090 руб.
Будущая стоимость через пять лет по схеме простых процентов равна 1000 90 • 5 = 1450 руб., где PV= 1000 руб., г = 0,09.
Будущая стоимость через пять лет по схеме сложных процентов (с капитализацией) составит, руб.:

В рассмотренном примере условиями размещения денежных средств второго случая (схема сложных процентов) предусмотрено, что инвестор вкладывает деньги на несколько лет под определенный процент.
Для одногодичного инвестирования разница в доходе между схемами простого и сложного процента отсутствует. С увеличением периода инвестирования разница начинает расти и становится огромной, например, для 100-летнего периода. При простом проценте увеличение стоимости идет по прямой равномерно. При сложном проценте наблюдается ускоренный рост накоплений. Кривая роста тем круче, чем выше ставка процента, длиннее срок инвестирования.
Для удобства расчета будущей стоимости применяют специальные таблицы, которые показывают будущую стоимость денежной единицы через п лет при соответствующей годовой процентной ставке. Фрагмент такой таблицы представлен в табл. 1.4.
Пример 1.2. Используя табл. 1.4, определим, в какую сумму превратится инвестируемая сумма в 1000 руб. инвестиционного проекта с неизменной ставкой 15% сроком на 10 лет. На пересечении строки 10 лет и столбца 15% таблицы показана сумма, в которую превратится 1 руб. через 10 лет, инвестированный но ставке 15% годовых. Эта цифра 4,046. Следовательно, для нашего примера будущая стоимость инвестиции составит, руб.:

Таблица 1.4
Будущая стоимость условной денежной единицы FVIF*
Год | Годовая процентная ставка | |||||||
1 | 2 | 5 | 6 | 10 | 15 | |||
1 | 1,010 | 1,020 | 1,050 | 1,060 | 1,100 | 1,150 | ||
2 | 1,020 | 1,040 | 1,102 | 1,124 | 1,210 | 1,323 | ||
3 | 1,030 | 1,061 | 1,158 | 1,191 | 1,331 | 1,521 | ||
4 | 1,041 | 1,082 | 1,216 | 1,262 | 1,464 | 1,749 | ||
5 | 1,051 | 1,104 | 1,276 | 1,338 | 1,611 | 2,011 | ||
10 | 1,105 | 1,219 | 1,629 | 1,791 | 2,594 | 4,046 | ||
15 | 1,161 | 1,346 | 2,079 | 2,397 | 4,177 | 8,137 | ||
20 | 1,220 | 1,486 | 2,653 | 3,207 | 6,727 | 16,37 | ||
*FVIF — future value interest factor.
Более сложен расчет будущей величины серии платежей. Общая формула такова, что каждый поток пересчитывается к будущему моменту времени, а затем общая выгода получается путем суммирования. Важный фактор, влияющий на получаемую выгоду, — срок поступления ожидаемого потока — начало или конец года. Традиционно предполагается, что денежные потоки приходят через один год от начала инвестирования, т.е. первое поступление от текущего момента отделяет временной лаг (например, в один год). Так, если инвестор предполагает получить по облигации в конце каждого инвестиционного года из трех по 50 руб., а в конце третьего года номинал равен 1000 руб., то общая сумма выгод на конец третьего года при принимаемой ставке процента с учетом риска 10% составит, руб.:

Данный расчет проведен для обычного аннуитета (ordinary, deferred annuity). Если поток поступает в начале периода, то он называется ранишь аннуитетом (annuity due).
Будущая оценка обычного аннуитета (FVA) на п годах при ставке процента на рынке г осуществляется по формуле

где РМТ (payment) — равный по номиналу денежный поток, приходящий на п периодах; FVAIFrn — табличное значение будущей оценки единичного аннуитета при ставке г и п периодах начисления.
Для обычных аннуитетных потоков (традиционное обозначение в финансовом калькуляторе — РМТ, payment) существуют специальные таблицы пересчета единичных потоков в будущие величины. Столбцами и строками этих таблиц являются процентные ставки и сроки жизни аннуитета. Например, будущая оценка единичного аннуитета в 10 лет при ставке 5% по таблице FVAIF$%10лет (см. прил. 5) составит 12,578.
Ранний аннуитет более выгоден инвестору, его будущая оценка выше обычного на величину (1 г), что очевидно из формулы

Зная текущую сумму инвестирования и будущую выгоду, можно найти соответствующую ставку процента, которая покажет, с какой стоимостью в процентах годовых инвестор сумел задействовать свои деньги.
Например, если первоначальная сумма капитала составила 100 руб., а через пять лет капитал равен 127,6 руб., то по таблице прил. 5 FVAIFx%, 5 лет очевидно, что ставка инвестирования равна 5% годовых. Именно эта ставка позволяет превратить за пять лет 1 д. е. в 1,276 д. е.
Для нахождения соответствующей ставки процента при инвестиционном горизонте больше одного года аналитики используют несколько приемов:
- 1) метод подбора;
- 2) выбор табличного значения (для разового потока или аннуитета);
- 3) финансовый калькулятор (предполагает введение периода получения выгод N, PV как отрицательной величины и FV) или программу Excel (финансовая функция ВСД);
- 4) применение упрощенных формул для потоков с определенными характеристиками (например, по типу облигационных платежей).
При инвестировании средств необходимо учитывать не только горизонт инвестирования, но и частоту процентных выплат. Кроме годового начисления процентов встречаются формы инвестиций, по которым проценты начисляются несколько раз в течение года. Самый яркий пример — банковские депозиты. В этом случае будущая стоимость рассчитывается по формуле

где т — число периодов начисления процентов в течении года.
Пример 1.3. Инвестор рассматривает варианты размещения 1000 руб. на банковском депозите сроком на один год, и условиями договора предусмотрено, что начисление процентов может осуществляться по полугодиям или ежемесячно с капитализацией процентов. Если годовая процентная ставка равна 12%, то за шесть месяцев начисляется 6%, или 1% ежемесячно.
Будущая стоимость годового депозита в первом случае составит, руб.:

Во втором случае, руб.:

Из примера 1.3 очевидно, что ежемесячное начисление процентов и их капитализация более выгодны. Если выплаты имеют место несколько раз в течение года, то фактически зарабатываемый процент оказывается больше, чем номинальная процентная ставка (в нашем примере 12% годовых). Номинальные и эффективные процентные ставки дают аналогичную выгоду при одноразовом начислении процентов (табл. 1.5).
Если выплаты осуществляются один раз в год, то номинальная процентная ставка, указанная в договоре, равна эффективному проценту (строка первая табл. 1.5, соответствующая одной выплате в году). Если же проценты начисляТаблица 1.5
Эффективные процентные ставки, %
Количество выплат в году | Номинальный процент | |||
5 | 10 | 15 | 20 | |
1 | 5 | 10 | 15 | 20 |
2 | 5,06 | 10,25 | 15,56 | 21,0 |
4 | 5,09 | 10,38 | 15,87 | 21,55 |
12 | 5,12 | 10,47 | 16,08 | 21,94 |
365 | 5,13 | 10,52 | 16,18 | 22,13 |
ются несколько раз в год и капитализируются, то эффективный процент больше номинальной процентной ставки. Например, если в договоре указана годовая процентная ставка 10%, а начисление процентов осуществляется ежеквартально, то фактически через год инвестор заработает 10,38%, а при ежемесячной капитализации соответствующая ставка уже составит 10,47% (соответствует 12 выплатам в году в табл 1.5 при номинальной ставке 10%).
Пример 1.4. Банк предлагает инвестору разместить валютный депозит под 5,1% годовых при разовом начислении процента или под 5% при ежемесячной капитализации. Из табл. 1.5 очевидно, что второй вариант более выгоден, так как фактически инвестор заработает 5,12% годовых (это и будет эффективная ставка рассматриваемого депозита).
Текущая стоимость может рассматриваться как расчетная величина из будущих ожидаемых выгод и упускаемых возможностей инвестирования. Количественно нахождение текущей стоимости разового потока реализуется через операцию дисконтирования:

где FV — будущая выгода; г — ставка процента на рынке или ставка дисконтирования; 1/(1 г) — коэффициент (множитель) дисконтирования; п — инвестиционный период (число лет).
В качестве ставки дисконтирования аналитики традиционно рассматривают доходность, которую можно получить на финансовом рынке, вкладывая деньги в какой-либо актив с аналогичным уровнем риска (облигации, банковский депозит, вексель и т.п.).
Пример 1.5. По дисконтной облигации через год ожидается получение 1000 руб. Если инвестор оценивает риск размещения средств в данную облигацию в 13% годовых, то справедливая цена облигации как текущая стоимость будущей выгоды составит, руб.:

В данном случае предполагается, что, купив данную облигацию за 885 руб. и получив через год при ее погашении 1000 руб., инвестор заработает требуемую доходность 13% годовых.
Для вычисления приведенной стоимости целесообразно пользоваться специальными таблицами дисконтирования, показывающими текущую стоимость разовой денежной единицы, которую предполагается получить через несколько лет (PVIF), или же приведенную стоимость обычного аннуитетного потока (PVAIF). Таблицы приведенных оценок даны в приложениях. Фрагмент таблицы для разового потока представлен в табл. 1.6.
Таблица 1.6
Приведенная стоимость денежной единицы (например, рубля), которая будет получена через п лет
Год | Годовая процентная ставка | |||||||
1 | 2 | 5 | 6 | 10 | 15 | |||
1 | 0,990 | 0,980 | 0,952 | 0,943 | 0,909 | 0,870 | ||
2 | 0,980 | 0,961 | 0,907 | 0,890 | 0,826 | 0,756 | ||
3 | 0,971 | 0,942 | 0,864 | 0,840 | 0,751 | 0,658 | ||
4 | 0,961 | 0,924 | 0,823 | 0,792 | 0,683 | 0,572 | ||
5 | 0,951 | 0,906 | 0,784 | 0,747 | 0,621 | 0,497 | ||
6 | 0,942 | 0,888 | 0,746 | 0,705 | 0,564 | 0,432 | ||
7 | 0,933 | 0,871 | 0,711 | 0,665 | 0,513 | 0,376 | ||
10 | 0,905 | 0,820 | 0,614 | 0,558 | 0,386 | 0,247 | ||
15 | 0,861 | 0,743 | 0,481 | 0,417 | 0,239 | 0,123 | ||
20 | 0,820 | 0,673 | 0,377 | 0,312 | 0,149 | 0,061 | ||
Пример 1.6. По табл. 1.6 определим текущую (приведенную) стоимость 800 руб., которые предполагается получить через четыре года при ставке дисконтирования 10% годовых. На пересечении строки (4 года) и столбца (10%) находим коэффициент дисконтирования, который равен 0,683. Это результат дисконтирования единичной выгоды. Текущая стоимость 800 руб. составит 800 • 0,683 = 546,4 руб.
Если проценты выплачивать чаще, чем один раз в год, то формула определения текущей стоимости модифицируется аналогично тому, как это проводилось для будущей стоимости. При многократном начислении процентов в течение года формула определения текущей стоимости принимает вид

Чем чаще происходит начисление процентов, тем меньше текущая стоимость при заданном конечном результате, т.е. взаимосвязь между частотой начисления процентов и текущей стоимостью обратна по сравнению с той, которая фиксировалась для будущей стоимости.
Приведенная стоимость потока платежей рассчитывается по формуле

Особый интерес для аналитиков представляет случай бессрочного аннуитета (бессрочной ренты), когда инвестор ожидает получать фиксированные выгоды в течение неограниченного периода времени.
Типичным примером таких выгод являются «британские консоли» (консолидированные облигации, выпущенные британским правительством, по которым инвесторы ежегодно получают 4,5 ф. ст.). Данные ценные бумаги не имеют срока погашения и, следовательно, инвестор в течение бесконечного отрезка времени рассчитывает получать фиксированный годовой доход.
Если известно ежегодное поступление денежных средств по активу, то текущая стоимость этого аннуитетного потока на бесконечном периоде времени определяется но формуле

Пример 1.7. Предположим, что инвестор по государственным ценным бумагам британского правительства с неограниченным сроком обращения рассматривает требуемую доходность на уровне 1%, по облигациям ежегодно выплачивается 4,5 ф. ст., тогда текущая стоимость облигации составит, ф. ст.:

Для срочного аннуитета расчет текущей стоимости осуществляется по формуле

Эта формула позволяет найти ежегодный аннуитетный поток, который соответствует текущей оценке инвестиционного проекта и заданной ставке доходности. Например, если известно, что текущая стоимость аннуитета равна 1000 долл., ставка стоимости денег — 4% годовых и период инвестирования — 10 лет, то требуемая сумма годовых платежей, которые обеспечат инвестору справедливый уровень отдачи, составит, долл.:

Отсюда сумма ежегодных равных платежей РМТ= 123,29 долл.
Как очевидно из формулы приведенной оценки срочного аннуитета, зная фиксированные ежегодные суммы и текущую оценку актива, можно рассчитать временной период, в течение которого актив будет окупаться. При фиксации временного горизонта и ежегодных выплат также может быть найдена исходная цена рассматриваемого актива, приносящего ежегодный доход.
Это направление расчетов очень широко применяется на практике, так как такие виды займов, как ссуды на приобретение недвижимости, автомобилей, потребительские кредиты, предусматривают поэтапное погашение заемщиком полученных ссуд. Расчет осуществляется таким образом, чтобы погашение «тела» ссуды и начисляемых процентов выполнялось равными по номиналу платежами в течение определенного срока при заданной процентной ставке. Такая схема погашения ссуды равными платежами называется амортизацией ссуды.
Пример 1.8. Российский инвестор считает приемлемым ежемесячный доход на пенсии в размере 40 000 руб. Ожидаемая государственная пенсия — 10 000 руб. и еще порядка 30 000 руб. в месяц инвестор рассчитывает получать из собственных накоплений. Потребность в годовой величине выплат в период нахождения на пенсии составляет для него 360 000 руб. Предположим, что инвестор оценивает период активного использования этих средств в 15 лет, а также, что на рынке имеются высоконадежный банк или страховая компания, которые предлагают полисы с выплатой ежегодно равных сумм при ставке процента 7% годовых. Сумма, которая должна быть внесена инвестором на депозит (покупку полиса), составит, тыс. руб.:

Облегчить задачу проведения расчетов позволяют аннуитетные таблицы PVAIF. Фрагмент таблицы аннуитетов представлен ниже (табл. 1.7).
Таблица 1.7
Приведенная стоимость аннуитетного потока в 1 д. е.
Период | Годовая процентная ставка | ||||||||
1 | 2 | 5 | 6 | 7 | 8 | 15 | |||
1 | 0,990 | 0,980 | 0,952 | 0,943 | 0,935 | 0,926 | 0,870 | ||
2 | 1,970 | 1,942 | 1,859 | 1,833 | 1,808 | 1,783 | 1,626 | ||
3 | 2,941 | 2,844 | 2,723 | 2,673 | 2,624 | 2,577 | 2,283 | ||
4 | 3,902 | 3,808 | 3,546 | 3,465 | 3,387 | 3,312 | 2,855 | ||
5 | 4,853 | 4,713 | 4,329 | 4,121 | 4,100 | 3,993 | 3,352 | ||
10 | 9,471 | 8,983 | 7,772 | 7,360 | 7,024 | 6,710 | 5,019 | ||
15 | 13,87 | 12,85 | 10,38 | 9,712 | 9,108 | 8,559 | 5,847 | ||
20 | 18,05 | 16,35 | 12,46 | 11,47 | 10,59 | 9,818 | 6,259 | ||
Предположим, что инвестор в примере 1.8 сократил срок получения дополнительной пенсии с 15 до 10 лет. По табл. 1.7 расчет примет следующий вид:

т.е. 360 • 7,024 = 2529 руб. Теперь инвестору достаточно вложить 2529 руб.
Пример 1.9. Компания получила от банка кредит в размере 150 млн руб. сроком на четыре года под 8% годовых. Условиями договора предусмотрено, что ссуда погашается поэтапно четырьмя равными платежами в течение четырех лет. Данная схема погашения представляет собой аннуитетный поток. В начальный момент времени банк передал компании 150 млн руб., а компания далее четыремя платежами гасит этот заем. Таким образом, 150 млн руб. должны рассматриваться как текущая (приведенная) оценка этих равных четырех платежей. Для определения суммы платежа воспользуемся данными таблицы приведенной оценки аннуитета. Множитель дисконтирования составляет 3,312. Следовательно, текущая стоимость аннуитета 150 = РМТ- 3,312.
Сумма годового платежа, позволяющего рассчитаться с банком, составляет, млн руб.:

Заметим, что сумма рассчитанного платежа в 45,29 млн руб. состоит из двух частей: одна из них используется для погашения основной суммы долга, а другая — для выплаты процентов. Проценты начисляются на остаток непогашенных средств на начало каждого года. Особенностью поэтапного погашения ссуды является то, что в первые годы процентные выплаты достаточно велики, а сумма погашаемого долга относительно мала. По мере приближения к сроку погашения всей ссуды процентные платежи уменьшаются, а сумма погашения основного долга возрастает.
Предположение о постоянном темпе роста прогнозируемых денежных выплат (выгод) позволяет ввести понятие растущего аннуитета. Растущий аннуитет — поток денежных выплат, которые возрастают от периода к периоду с заданным фиксированным темпом роста. В финансовых расчетах широко применяется формула приведенной оценки бесконечно растущего аннуитета:

где РМТ — начальная денежная выплата, с которой начинается рост; РМТ( 1 g) — первый ожидаемый денежный выигрыш (платеж); g — фиксированный на всем временном горизонте темп прироста выгод; г — ставка процента на рынке.
Чистая приведенная стоимость (NPV). Приведенная оценка будущих денежных выгод позволяет сопоставить варианты инвестирования с разными потребностями в инвестициях. Каждый раз инвестор принимает решение о вложении средств, соотнося предполагаемые суммарные выгоды (как приведенную оценку выгод) с величиной требуемых инвестиций.
Разность между суммарными выгодами и требуемыми инвестициями трактуется как чистый эффект инвестирования, или чистая приведенная стоимость.
Чистую приведенную стоимость вычисляют как разницу между суммарной приведенной стоимостью ожидаемых денежных выгод (их текущей оценкой) и потребностью в инвестициях:

где Со — инвестиционные затраты (обычно предполагается приведенная оценка инвестиционных затрат, фиксируемых в разные временные периоды); С„ — текущие денежные выгоды от инвестирования по годам, например годовая прибыль или денежные потоки; г — ставка процента, соответствующая уровню риска инвестирования (ставка дисконтирования); t — число лет до окончания проекта.
Инвестиционный вариант рассматривается как более привлекательный, если он обеспечивает большее значение NPV.
Методы встраивания факторов риска в конструкцию дисконтирования ожидаемых выгод. Корректными можно признать три варианта включения риска в формулу дисконтирования выгод. Два наиболее популярных метода показаны на рис. 1.8. В академической литературе и на практике преимущество отдается первому методу — через корректировку ставки дисконтирования. Традиционно выявляются систематические риски актива и обосновывается премия за риск (risk premium). Чем больше систематический риск по ожидаемым денежным потокам, тем в большую сторону увеличивается ставка дисконтирования по сравнению с безрисковой ставкой.

Рис. 1.8.Наиболее популярные методы встраивания факторов риска в конструкцию дисконтирования ожидаемых выгод
Подчеркнем, что только факторы рыночного риска (инфляция, цены на сырье для ресурсных компаний) порождают корректировку ставки дисконтирования[1]. Учет политических и технологических рисков в деятельности компании реализуется через коррекцию денежных потоков: оценка затрат на страхование и меры по снижению риска отражаются в операционных затратах с итоговым снижением прогнозируемых денежных выгод. Специфические риски компании с позиции диверсифицированного инвестора не требуют корректировок. При недиверсифицированной позиции инвестора целесообразно учитывать затраты на страхование в операционных затратах и понижать прогнозируемые денежные потоки.
Второй метод — корректировка денежного потока. В этом случае в качестве ставки дисконтирования выступает безрисковая рыночная ставка (например, ставка по государственным заимствованиям или ставка высоконадежных депозитов в первоклассных банках). Второй метод отражения риска носит название метода безрискового эквивалента (или метода риск-нейтрального денежного потока, эквивалентного гарантированного денежного потока, СЕ PV). Этот метод предполагает нахождение таких потоков денежных выгод, которые будут, с одной стороны, безрисковыми (т.е. получены инвестором со 100%-ной вероятностью), а с другой стороны — эквивалентными рискованным потокам, которые были спрогнозированы для инвестиционного объекта[2].
Третий метод — комбинированный, когда систематические риски включаются в ставку дисконтирования в виде премии за систематические риски, а сохраняющиеся специфические риски (уникальные, связанные с данным вариантом инвестирования) встраиваются в денежные потоки, корректируя их в меньшую сторону.
Репетитор оценщика – формулы сложных процентов
6 ФУНКЦИЙ
ДЕНЕЖНОЙ ЕДИНИЦЫ. ФОРМУЛЫ СЛОЖНЫХ ПРОЦЕНТОВ
Теория изменения стоимости денег
исходит из предположения, что деньги,
являясь специфическим товаром, со временем меняют
свою стоимость и, как правило, обесцениваются. Изменение стоимости денег
происходит под влиянием ряда факторов, важнейшими из которых можно назвать
инфляцию и способность денег приносить доход при условии их разумного
инвестирования в альтернативные проекты. Основными операциями, позволяющими
сопоставить разновременные деньги, являются операции накопления (наращивания) и
дисконтирования.
ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ
Накопление
– это процесс приведения текущей стоимости денег к их будущей стоимости, при
условии, что вложенная сумма удерживается на счету в течение определенного
времени, принося периодически накапливаемый процент.
Дисконтирование
– это процесс приведения денежных поступлений от инвестиций к их текущей
стоимости.
Аннуитетные
платежи (PMT) – это серия равновеликих платежей (поступлений), отстоящих
друг от друга на один и тот же промежуток времени. Выделяют обычный и авансовый аннуитеты. Если
платежи осуществляются в конце каждого периода, то аннуитет обычный, если в
начале – авансовый.
Текущая стоимость
(PV) (англ. Present value) – исходная сумма долга
или оценка современной величины денежной суммы, поступление которой ожидается в
будущем, в пересчете на более ранний момент времени.
Будущая
стоимость (FV)(англ. Future value) – сумма
долга с начисленными процентами в конце срока.
Ставка дохода или процентная
ставка (i) (англ. Rate of interest) – является относительным показателем
эффективности вложений (норма доходности), характеризующим темп прироста
стоимости за период.
Срок погашения долга (n) (англ. Number of
periods) – интервал времени, по истечении которого сумму долга и проценты нужно
вернуть. Срок измеряется числом расчетных периодов, обычно равных по длине
(например, месяц, квартал, год), в конце которых регулярно начисляются
проценты.
Частота
накоплений в год (k)– периодичность начисления процентовоказывает влияние на величину накопления.
Чем чаще начисляются проценты, тем больше накопленная сумма.
ОБОЗНАЧЕНИЯ К ФОРМУЛАМ
FV
– будущая стоимость денежной единицы;
PV
– текущая стоимость денежной единицы;
PMT – равновеликие периодические платежи;
i
– ставка дохода или процентная ставка;
n
– число периодов накопления, в годах;
k
– частота накоплений в год.
6 ФУНКЦИЙ ДЕНЕЖНОЙ ЕДИНИЦЫ
 Формула сложных процентов – 1 функция
Формула сложных процентов – 1 функция
Будущая
стоимость денежной единицы (FV) –
накопленная сумма денежной единицы. Накопленная
сумма денежной единицы показывает, какую сумму будет составлять денежная
единица, вложенная сегодня, через определенный период времени при определенной
ставке дисконта (доходности).
Начисление
процентов 1 раз в год: = PV* [(1 i)n] или FV = PV* кол.1
Начисление
процентов чаще, чем один раз в год: FV = PV* [(1 i/k)nk]
 Формула сложных процентов – 2 функция
Формула сложных процентов – 2 функция
Текущая
стоимость денежной единицы (PV) или текущая стоимость реверсии
(перепродажи) показывает, какую сумму
нужно иметь сегодня, чтобы через определенный период времени при определенной
ставке дисконта (доходности) получить сумму, равную денежной единице, то есть
какой сумме сегодня эквивалентна денежная единица, которую мы рассчитываем
получить в будущем через определенный период времени.
Текущая стоимость аннуитетапоказывает, какой сумме денежных средств сегодня эквивалентна
серия равномерных платежей в будущем, равных одной денежной единице, за
определенное количество периодов при определенной ставке дисконта.
Выделяют обычный и авансовый аннуитеты. Если платежи осуществляются в конце
каждого периода, то аннуитет обычный, если в начале – авансовый.
Обычный аннуитет:
Накопление денежной единицы за период FV –
будущая
стоимость серии равновеликих периодических платежей (поступлений). Фактор
накопления единицы за период показывает, какой будет стоимость серии равных
сумм, депонированных в конце каждого периодического интервала по истечении
установленного срока.
Взнос на амортизацию денежной единицы – это величина
регулярного периодического платежа в счет погашения кредита, выданного
на определенный период при процентной заданной ставке. Это величина,
обратная текущей стоимости аннуитета. Амортизация в данном случае – это
погашение (возмещение, ликвидация) долга в течение определенного времени.
Начисление процентов чаще, чем один раз в год: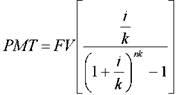
См. таблицы сложных процентов. 6 функций денежной единицы
Примеры решения задач по “Экономике недвижимости”






