Задачи для самостоятельного решения — студопедия
Таблица 1 — Денежный поток по проекту, у. е.
| Год | 0 | 1 | 2 | 3 | 4 | 5 |
| Денежные потоки | -1500 | 200 | 400 | 400 | 600 | 700 |
Методические указания:
| Дано: К = 1500 у. е. Dt — в табл. 3.1.1 n = 5 лет ____________________ РР =? | Решение: Считаем сумму доходов нарастающим итогом до тех пор, пока она не превысит капиталовложения: сумма доходов за первые 3 года составляет 200 400 400 = 1000 у е. что недостаточно для покрытия инвестиций; |
сумма доходов за первые 4 года составляет
200 400 400 600 = 1600 у. е., что покрывает инвестиции с избытком, т. е. срок окупаемости — 4 года.
Найдем более точно срок окупаемости:
через 3 года непокрытый остаток капиталовложений (Кост) равен:
Кост = K — (D1 D2 D3) = 1500 — 1000 = 500 у. е.,
который может быть покрыт за 0,83 (500/600) четвертого года, т. е. за 10 (0,83  12) месяцев.
12) месяцев.
Ответ:Срок окупаемости инвестиций 3 года и 10 месяцев.
Задача 3.В инвестиционный проект предлагается вложить 1600 у. е. Обещанный среднегодовой доход составляет 400 у. е. Ожидается, что ставка доходности (дисконтирования) не будет меняться и будет составлять 10 % годовых. Найти абсолютный и дисконтированный срок окупаемости.
Методические указания:
| Дано: K = 2 тыс. у. е. Dср = 400 у. е. r = 0,1 _____________ Р P = ? DPP = ? | Решение: Абсолютный срок окупаемости находится непосредственно из формулы (3.1.1), т. к. поток доходов равномерный: РР=К/ Dср = 1600/400 = 4 года. |
Для расчета дисконтированного срока окупаемости считаем сумму дисконтированных доходов нарастающим итогом до тех пор, пока она не превысит капиталовложения. Сумма доходов за первые 5 лет составляет:
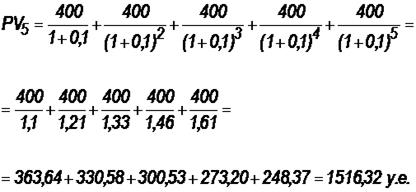
что меньше суммы капиталовложений.
Сумма доходов за первые 6 лет составляет:
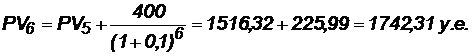 , что покрывает исходную сумму капиталовложений, т. е. срок окупаемости — 6 лет.
, что покрывает исходную сумму капиталовложений, т. е. срок окупаемости — 6 лет.
Более точно:
через 5 лет непокрытый остаток капиталовложений (Кост) равен:
Кост = K — PV 5 = 1600 — 1516,32 = 83,68 у. е.,
который может быть покрыт за 0,37 (83,68/225,99) шестого года, т. е. за 4,4 (0,37  12) месяца.
12) месяца.
Ответ:Абсолютный срок окупаемости инвестиций составит 4 года; дисконтированный срок окупаемости — 5 лет и 4,4 месяца.
Задача 4.Компания N располагает двумя альтернативными вариантами инвестиционных проектов, требующих одинаковых вложений. Данные, характеризующие эти проекты, приведены в табл. 3.1.2 и на рис. 3.1.1. Найти срок окупаемости инвестиций для каждого из проектов. Выбрать проект для реализации с точки зрения: а) сохранения ликвидности; б) получения дохода; в) эффективности. Принять решение на основе учетных оценок.
Таблица 2 — Денежные потоки по проектам, А и Б, у. е.
Денежные потоки по проектам | Год | ||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| Проект, А | -1000 | 150 | 200 | 300 | 400 | 500 | 600 |
| Проект Б | -1000 | 500 | 400 | 300 | 100 | — | — |
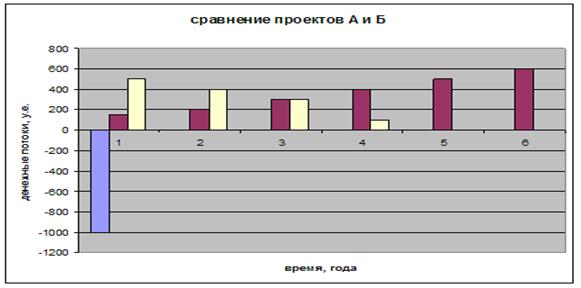
Рис.1 — денежные потоки по проектам, А и Б: синим цветом обозначены вложения, коричневым — денежные потоки для проекта А; желтым — денежные потоки для проекта Б.
Методические указания:
| Дано: Dt — в табл. 3.1.2 nА = 6 лет nБ = 4 года r = 0,1 ________________ РР = ? D = ? ARR = ? | Решение: 1. Решим задачу на основе учетных (не дисконтированных) оценок. Срок окупаемости проекта, А: Считаем сумму доходов нарастающим итогом до тех пор, пока она не превысит капиталовложения: сумма доходов за первые 3 года составляет 150 200 300 = 650 у. е., что недостаточно для покрытия инвестиций; сумма доходов за первые 4 года составляет 650 400 = 1050 у. е., что покрывает инвестиции с избытком, т. е. срок окупаемости, согласно формуле (3.1.2), — 4 года. |
Найдем более точно срок окупаемости:
через 3 года непокрытый остаток капиталовложений (Кост) равен:
Кост = K — (D1 D2 D3) = 1000 — 650 = 350 у. е.,
который может быть покрыт за 0,875 (350/400) четвертого года, т. е. за 10,5 (0,875  12) месяцев.
12) месяцев.
Таким образом, срок окупаемости проекта, А составляет 3 года и 10,5 месяца.
Аналогичным образом находим срок окупаемости проекта Б — 3 года, а более точно:
Кост = K — (D1 D2) = 1000 — (500 400) = 100 у. е.,
который может быть покрыт за 0,33 (100/300) третьего года, т. е. за 4 (0,33  12) месяца.
12) месяца.
Таким образом, срок окупаемости проекта Б составляет 2 года и 4 месяца.
Рассчитаем общий доход (D) по проектам:
DA = 150 200 300 400 500 600 = 2150 у. е.
DБ = 500 400 300 100 = 1300 у. е.
Эффективность проекта можно оценить путем расчета коэффициента эффективности инвестиций, для чего необходимо рассчитать среднегодовую прибыль (Р) и среднегодовую стоимость эксплуатируемых инвестиций (I):
PA = (DA — KA)/nА = (2150 — 1000)/6 = 191,7 у. е.
PБ = (DБ — KБ)/nБ = (1300 — 1000)/4 = 75 у. е.
Среднегодовая стоимость эксплуатируемых инвестиций у обоих проектов одинаковая:
I = K/2 = 1000/2 = 500 у. е.
Коэффициент эффективности инвестиций:
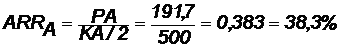
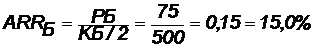
Ответ:С точки зрения ликвидности (по сроку окупаемости) более предпочтителен проект Б, окупающийся через 2 года и 4 месяца, чем проект, А, окупающийся за 3 года и 10,5 месяца. Однако проект, А приносит больше дохода (2150 у. е.), чем проект Б, (1300 у. е.) Проект, А также более эффективен ( 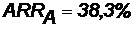 ), чем проект Б (
), чем проект Б ( 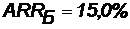 ).
).
Задача 5.Рассматривается вопрос о приобретении одной из двух машин, А и B. Ожидается, что их эксплуатация будет приносить доход в течение 2 и 3 лет соответственно (табл. 3). Альтернативные издержки равны 10 %. Вычислите чистую приведенную стоимость каждой машины. Какую машину следует купить?
Таблица 3 — Потоки денежных средств для проектов А и В, руб.
Методические указания:
Исходя из показателя чистой приведенной стоимости, следует выбрать машину В, т. к. NPV у этого проекта больше. Однако следует помнить, что критерий NPV используется при сравнении равномасштабных проектов. Здесь проекты имеют разные масштабы как с точки зрения вложений, так и срока эксплуатации. Поэтому необходимо привлечь критерий рентабельности инвестиций — PI:
PI = PV / K = (NPV K) / K.
PI (A) = (100 100) / 100 = 2 = 200 %;
PI (B) = (180 120) / 120 = 2,5 = 250 %.
По данному критерию также следует отдать предпочтение проекту В.
Ответ:Следует выбрать машину В.
Задача 6.У компании имеются два проекта -А и Б. Каждый проект имеет издержки в 10 тыс. р., альтернативные издержки для каждого проекта составляют 12 %. Ожидаемые денежные потоки, генерируемые этими проектами представлены в таблице 3.1.4.
Таблица 4 — Денежные потоки по двум проектам, А и Б
| Год | Проект, А (тыс. р.) | Проект Б (тыс. р.) |
| 0 | -10 тыс. | -10 тыс. |
| 1 | 6500 | 3500 |
| 2 | 3 тыс. | 3500 |
| 3 | 3 тыс. | 3500 |
| 4 | 1000 | 3500 |
Задания:
а) подсчитать период окупаемости, чистую приведенную стоимость, коэффициент внутренней нормы доходности для каждого проекта;
б) решить, какой проект должен быть принят, если они независимые;
в) решить, какой проект должен быть принят, если они взаимоисключаемые;
г) оценить, как изменение ставки дисконтирования могло бы привести к конфликту в ранжировании этих двух проектов по чистой приведенной стоимости и по внутренней норме доходности;
д) ответить на вопрос, какой проект предпочтительнее – при r = 4,5 % или при r = 8 %?
Методические указания:
Т. к. ожидаемый поток доходов меняется из года в год, период окупаемости можно определить, суммируя доходы по годам до тех пор, пока их сумма не станет равной первоначальному вложению. Через 2 года накопленный доход 9,5 тыс. р. (6,5 3) меньше капвложений, через 3 года – 12,5 тыс. р. (6,5 3 3) — больше.
Точный расчет срока окупаемости:
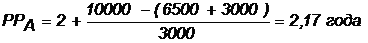
Аналогичный расчет сделаем для проекта Б.
Окупаемость проекта Б (лет):
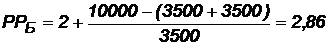 года.
года.
При независимости оба проекта следует принять, т. к. срок окупаемости не превышает срока эксплуатации проектов. Если следует выбрать один, то более предпочтительным оказывается проект, А, имеющий меньший срок окупаемости.
2. Чистая приведенная стоимость:

При независимости оба проекта следует принять, т. к. NPV для обоих проектов положителен. Если следует выбрать один, то более предпочтительным оказывается проект, А, имеющий больший чистый дисконтированный доход.
3. Внутренняя норма доходности:
Для расчета внутренней нормы доходности воспользуемся приблизительным расчетом на основе формулы:
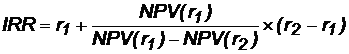 .
.
В качестве r1 используем исходную ставку дисконтирования 12 %. В качестве r2 возьмем, например, 20 %.
Рассчитаем NPV со ставкой 20 %:

При независимости проекты следует принять, если PI не превышает стоимости привлекаемых средств. Если следует выбрать один, то более предпочтительным оказывается проект, А, имеющий большую внутреннюю норму доходности.
б)По всем рассмотренным критериям оба проекта являются приемлемыми. Таким образом, оба проекта должны быть приняты, если они независимые.
в)При альтернативности проектов выбрать следует проект А. Он лучше по всем показателям.
г)Найдем r, при котором NPV двух проектов равны (точку Фишера):
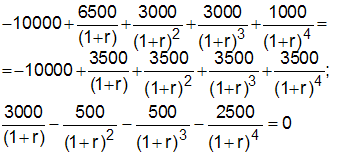
Домножим обе части уравнения на 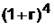 :
:
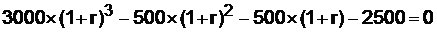
Подставим в левую часть r = 6 % и r = 7 %. В первом случае левая часть уравнения:
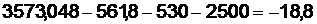
Во втором случае:
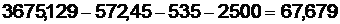
Теперь возьмем 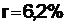 :
:
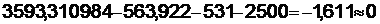 .
.
Поскольку существует точка Фишера, конфликт критериев при выборе инвестиционного проекта возможен.
Если r < 6,2 %, то проект Б, худший по критерию IRR, оказывается лучшим по критерию NPV (см. рис. 2).
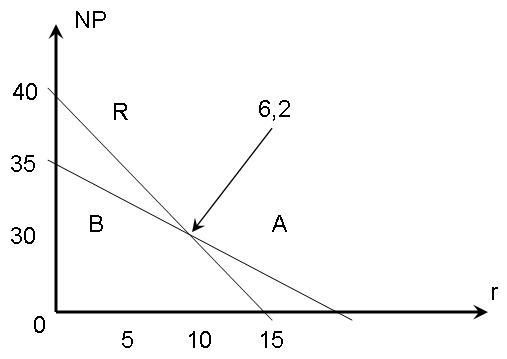
Рис. 2 — Точка Фишера
д)Если стоимость капитала фирмы 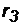 = 4,5 %, то, поскольку 4,5 % < 6,2 %, существует конфликт: по критерию NPV лучше проект Б, поскольку
= 4,5 %, то, поскольку 4,5 % < 6,2 %, существует конфликт: по критерию NPV лучше проект Б, поскольку 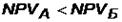 (это видно на графике), а по критерию IRR лучше проект А, поскольку
(это видно на графике), а по критерию IRR лучше проект А, поскольку  .
.
В подтверждение проведем расчет NPV со ставкой 4,5 %:
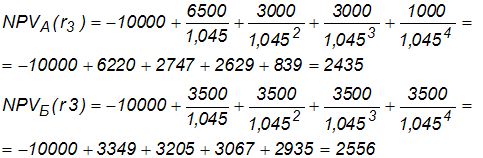
Ответ: По всем рассмотренным критериям оба проекта являются приемлемыми. Таким образом, оба проекта должны быть приняты, если они независимые. Если проекты альтернативные, то выбрать следует проект А. При снижении ставки дисконтирования ниже 6,2 % возникает конфликт критериев: проект, А становится хуже проекта В по критерию чистой дисконтированной стоимости.
Задача 7.
Вычислите чистую текущую стоимость (чистый дисконтированный доход) и индекс прибыльности (коэффициент рентабельности) каждого следующего вида инвестиций (табл. 3), если требуемая альтернативная ставка равна 10 %. Предполагается, что каждый вид инвестиций может потребовать использования одного и того же участка земли. Следовательно, можно осуществить только один из них. Какой?
Таблица 5 — Денежные потоки по четырем видам инвестиций
Методические указания:

Ответ: Наибольшая чистая приведенная стоимость у первого проекта. Если мы хотим наращивать стоимость компании, то нужно выбрать проект 1, т. к. у него самая большая приведенная стоимость. А если нужно получить более высокую норму доходности, то проект 4, поскольку у него наибольший индекс прибыльности.
Задача 8.Размер инвестиции, произведенный к началу первого года эксплуатации проекта, составил 115 тыс. $. Доходы от инвестиций распределены по годам следующим образом: в первом году — 32 тыс. $; во втором — 41 тыс. $; в третьем — 43750 $; в четвертом — 38250 $. Рассчитайте внутреннюю норму доходности и модифицированную внутреннюю норму доходности и примите решение о приемлемости проекта, если реальная ставка дисконтирования равна 6,6 %.
Методические указания:
Рассчитаем общий дисконтированный доход:
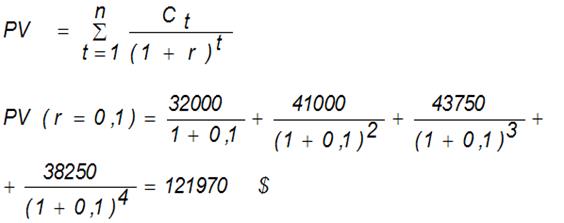
Чистый дисконтированный доход:
NPV (r = 0,1) = PV — K = 121 970 — 115 000 = 6970 $.
Для приблизительного расчета внутренней нормы доходности рассчитаем NPV для ставки, равной 15 %:
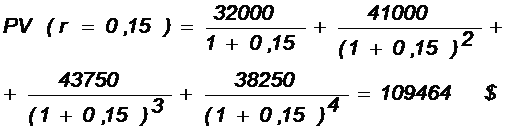
NPV (r = 0,15) = 109 464 — 115 000 = -5536 $
Внутренняя норма доходности:
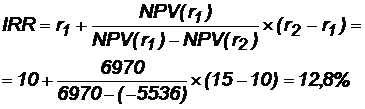
Модифицированная норма доходности находится из условия:
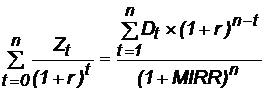
В связи с тем что оттоки в нашем случае имеют место только в начальный момент, формула упрощается:
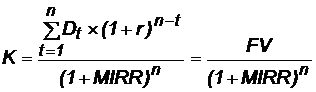
откуда 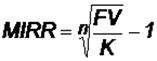
Рассчитаем общий будущий (наращенный) доход:
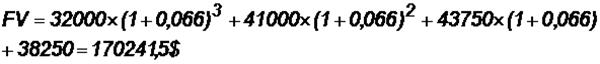
Рассчитаем MIRR:
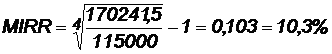
Ответ: Модифицированная внутренняя норма доходности равна 10,3 %, что больше нормы реинвестиций (6,6 %). Это означает, что проект можно реализовать. Коэффициент окупаемости (внутренняя норма доходности) равен 12,8 %, что означает, что можно привлекать средства по цене не более чем 12,8 %.
Задача 9.Коммерческая организация рассматривает целесообразность приобретения новой технологической линии. Стоимость линии составит 10 млн $; срок эксплуатации — 5 лет; износ на оборудование начисляется методом линейной амортизации. Выручка от реализации продукции прогнозируется по годам в следующих объемах (в тыс. $): 6800, 7400, 8200, 8 тыс., 6 тыс.. Текущие расходы по годам оцениваются следующим образом: 3400 тыс. $ в первый год эксплуатации линии с последующим ежегодным ростом их на 3 %. Ставка налога на прибыль составляет 24 %. Сложившееся финансово-хозяйственное положение коммерческой организации таково, что коэффициент рентабельности авансированного капитала составлял 21 % стоимость авансированного капитала (WACC) — 19 %. В соответствии со сложившейся практикой принятия решений в области инвестиционной политики руководство организации не считает целесообразным участвовать в проектах со сроком окупаемости более 4 лет. Целесообразно ли реализовать данный проект?
Методические указания:1) рассчитать денежный поток; 2) использовать все возможные критерии; 3) ввести дополнительные обозначения: В — выручка, Р — текущие расходы, А — амортизационные отчисления (износ), НП — налогооблагаемая прибыль, СНП — ставка налога на прибыль, ЧП — чистая прибыль.
| Дано: К = 10 млн $ n = 5 лет В = {6800, 7400, 8200, 8 000, 6 000} тыс.$ Р1 = 3400 тыс.$ 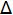 P = 0,03 в год P = 0,03 в годСНП = 0,24 d = 0,21 WACC = 0,19 PPн < 4 года _______________________ Целесообразность проекта? | Решение: В соответствии с приведенными условиями денежный поток по годам включает в себя: приток — выручка, оттоки — текущие расходы и налог на прибыль. Таким образом, чистый денежный поток равен: D = В — Р — НП = ЧП А. НП = П  СНП, в свою очередь: СНП, в свою очередь:П = В — Р — А. Для расчета амортизационных отчислений используется линейный метод, в соответствии с которым ежегодная сумма амортизации определяется как: А = К / n = 10 000 / 5 = 2000 $. |
Рассчитаем денежный поток первого года:
П1 = В1 — Р1 — А1 = 6800 — 3400 — 2000 = 1400 тыс. $;
НП1 = П1 СНП = 1400
СНП = 1400  0,24 = 336 тыс.$;
0,24 = 336 тыс.$;
D1= В1 — Р1 — НП1 = 6800 — 3400 — 336 = 3064 тыс. $.
Или иначе: ЧП1 = П1 — НП1 = 1400 — 336 = 1064 тыс.$;
D1 = ЧП1 А = 1064 2000 = 3064 тыс. $.
Для расчета денежного потока второго и последующих лет необходимо рассчитать величину текущих затрат:
Р2 = Р1 (1
(1 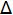 P) = 3400
P) = 3400  (1 0,03) = 3502 тыс. $;
(1 0,03) = 3502 тыс. $;
Р3 = Р2 (1
(1 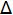 P) = 3502
P) = 3502  (1 0,03) = 3607 тыс. $ и т. д.
(1 0,03) = 3607 тыс. $ и т. д.
Все расчеты денежного потока представлены в табл. 3.1.6.
Таблица 6. — Расчет чистого денежного потока по проекту
Показатели | Годы | ||||
| 1-й | 2-й | 3-й | 4-й | 5-й | |
| Объем реализации (В) | 6800 | 7400 | 8200 | 8 тыс. | 6 тыс. |
| Текущие расходы (Р) | 3400 | 3502 | 3607 | 3715 | 3827 |
| Износ (А) | 2 тыс. | 2 тыс. | 2 тыс. | 2 тыс. | 2 тыс. |
| Налогооблагаемая прибыль (П) | 1400 | 1898 | 2593 | 2285 | 173 |
| Налог на прибыль (НП) | 336 | 456 | 622 | 548 | 42 |
| Чистая прибыль (ЧП) | 1064 | 1442 | 1971 | 1736 | 132 |
| Чистые денежные поступления (D) | 3064 | 3442 | 3971 | 3736 | 2132 |
Рассчитаем критерии, основанные на учетных оценках.
Первый — срок окупаемости:
за 2 года накопленный доход составит 6506 тыс. $, что меньше стоимости технологической линии;
за 3 года накопленный доход составит 10 477 тыс. $, т. е. немногим более стоимости технологической линии, т. е. за три года инвестиции полностью окупаются (рис. 3.1.3).
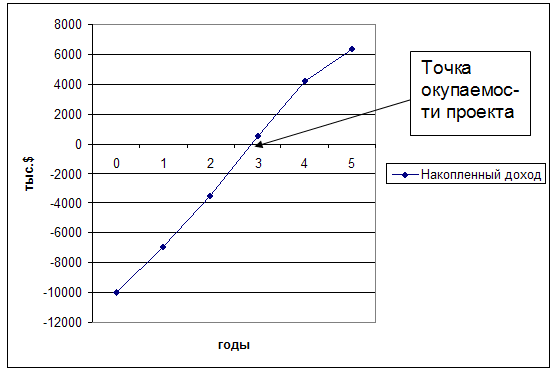
Рис. 3 — Накопленный доход и срок окупаемости проекта
РР < РРн, т. е. максимально возможный срок окупаемости (4 года) больше расчетного, следовательно, проект приемлем.
Второй критерий — оценка эффективности инвестиций:
cреднегодовая прибыль:
ЧПср = (1064 1442 1971 1736 132) / 5 = 3269 тыс. $;
cреднегодовая стоимость эксплуатируемых инвестиций:
I = (K S)/2 = (10 000 0)/2 = 5 тыс. тыс. $;
коэффициент эффективности инвестиций:
ARR = 3269 / 5 тыс. = 0,654 = 65,4 %.
ARR > d, т. е. эффективность проекта выше эффективности предприятия, поэтому проект приемлем.
Теперь рассмотрим критерии, основанные на дисконтированных оценках. Первый — общий дисконтированный доход:
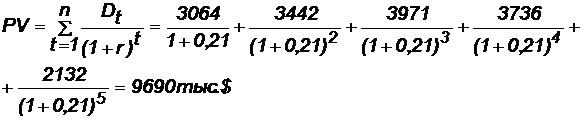
PV < K, следовательно, проект неприемлем.
На рис. 3.1.4 представлены поступления по годам: принимаемые к учету и дисконтированные.
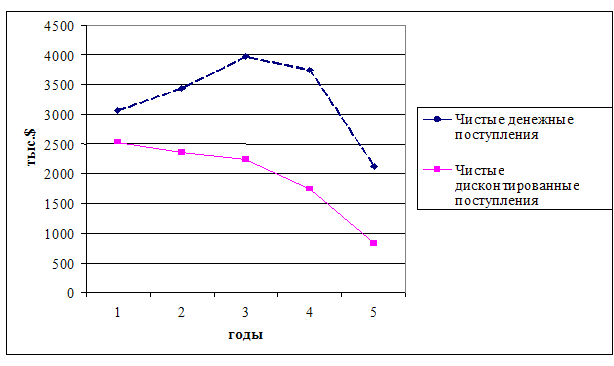
Рис.4 — Чистые денежные поступления по проекту
Второй критерий — чистый дисконтированный доход:
NPV = PV — K = 9690 — 10 000 = -310 тыс. $.
NPV < 0, следовательно проект неприемлем.
Следующий критерий — индекс доходности инвестиций:
PI = PV / K = 9690 / 10 000 = 0,969.
PI < 1, следовательно, проект неприемлем.
Еще один критерий — внутренняя норма доходности (рентабельности). Для нахождения IRR на основе формулы (3.1.11) найдем NPV с уменьшенной ставкой дисконтирования (например, 18 %):
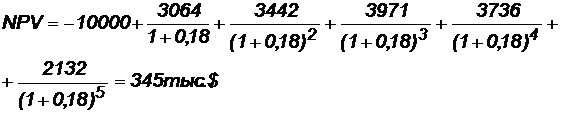
Теперь найдем IRR:
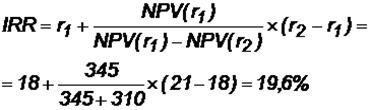
IRR < WACC, следовательно, проект неприемлем.
Для расчета модифицированной нормы доходности необходимо рассчитать общий наращенный доход (см. задачу 8):
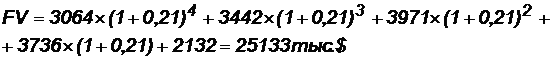
Модифицированную норму доходности найдем по формуле:
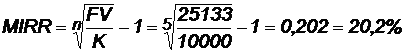
MIRR < WACC, следовательно, проект неприемлем.
Последний критерий — дисконтированный срок окупаемости.
За все 5 лет эксплуатации технологической линии общий дисконтированный доход (9690 тыс.$) не покрывает первоначальных инвестиций (10 000 тыс.$), т. е. проект не окупается(рис. 3.1.5) и, следовательно, он неприемлем.
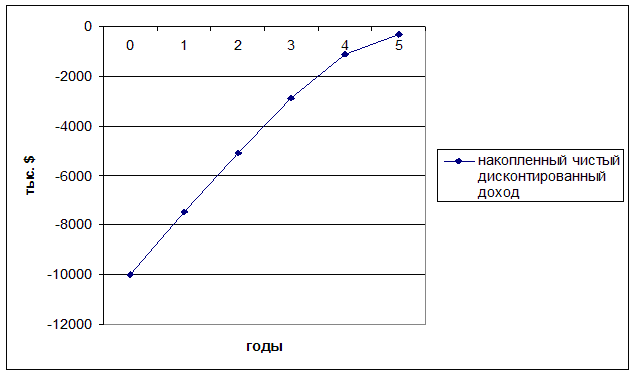
Рис. 5 — Накопленный чистый дисконтированный доход
Ответ: На основе учетных оценок критерий можно считать приемлемым. При использовании дисконтирования проект следует отвергнуть. В реальной практике следует ориентироваться на какой-то один или несколько критериев, наиболее важных, по мнению руководителей коммерческой организации, либо принять во внимание дополнительные объективные и субъективные факторы.
Задачи для самостоятельного решения
Задача 10.Инвестор желает вложить денежные средства в строительство предприятия, которое предполагается эксплуатировать 20 лет. Инвестиции, общей суммой 10 000 тыс. р., решено вкладывать поэтапно в начале каждого года строительства предприятия в течение 3 лет: в 1-й год — 3000 тыс. р.; во 2-й — 2000 тыс. р.; в 3-й — 5000 тыс. р. По окончании 3 лет строительства предприятие будет построено, введено в эксплуатацию и начнет производить продукцию, ожидаемый ежегодный доход (выручка) от которой намечается в размере 4000 тыс. р. при ежегодных текущих затратах 2000 тыс. р. Инвестор считает, что учетная ставка Центрального банка РФ в период строительства предприятия будет равна 12 % годовых, а в период эксплуатации предприятия — 10 % годовых.
Какова целесообразность вложения инвестиций в строительство предприятия?
Методические указания: 1) Оценить инвестиционный проект по всем возможным критериям с учетом и без учета дисконта денежных потоков; 2) Результаты расчета денежных потоков представить на графиках суммарной величины дисконтируемых и недисконтируемых денежных потоков в зависимости от времени.
Задача 11.Рассматривается проект строительства предприятия, которое предполагается эксплуатировать 20 лет. Инвестиции, общей суммой 10 000 тыс. р., решено вкладывать поэтапно в начале каждого года строительства предприятия в течение 3 лет: в 1-й год — 5000 тыс. р.; во 2-й — 3000 тыс. р.;в 3-й — 2000 тыс. р. По окончании 3 лет строительства предприятие будет построено, введено в эксплуатацию и начнет производить продукцию, ожидаемый ежегодный доход (выручка) от которой намечается в размере 5000 тыс. р. при ежегодных текущих затратах 2000 тыс. р. Инвестор считает, что учетная ставка Центрального банка РФ в период строительства предприятия будет равна 11 % годовых, а в период эксплуатации предприятия — 10 % годовых.
Оценить целесообразность вложения инвестиций в строительство предприятия.
Методические указания: 1) Оценить инвестиционный проект по всем возможным критериям с учетом и без учета дисконта денежных потоков; 2) Результаты расчета денежных потоков представить на графиках суммарной величины дисконтируемых и не дисконтируемых денежных потоков в зависимости от времени.
Задача 12.Необходимо принять решение о вложении денежных средств в строительство предприятия, которое предполагается эксплуатировать 18 лет. Инвестиции, общей суммой 10 000 тыс. р., решено вкладывать поэтапно в начале каждого года строительства предприятия в течение 3 лет: в 1-й год — 3000 тыс. р.; во 2-й — 3000 тыс. р.; в 3-й — 4000 тыс. р. По окончании 3 лет строительства предприятие будет построено, введено в эксплуатацию и начнет производить продукцию, ожидаемый ежегодный доход (выручка) от которой намечается в размере 4000 тыс. р. при ежегодных текущих затратах 2200 тыс. р. Инвестор считает, что учетная ставка Центрального банка РФ в период строительства предприятия будет равна 10 % годовых, а в период эксплуатации предприятия — 8 % годовых.
Методические указания: 1) Оценить инвестиционный проект по всем возможным критериям с учетом и без учета дисконта денежных потоков; 2) Результаты расчета денежных потоков представить на графиках суммарной величины дисконтируемых и недисконтируемых денежных потоков в зависимости от времени.
Задача 13.Инвестор рассматривает вопрос о целесообразности строительства предприятия, которое предполагается эксплуатировать 25 лет. В соответствии с графиком строительства вложения осуществляются поэтапно в начале каждого года строительства предприятия в течение 3 лет: в 1-й год — 4000 тыс. р.; во 2-й — 3000 тыс. р.; в 3-й — 3000 тыс. р. По окончании 3 лет строительства предприятие будет построено, введено в эксплуатацию и начнет производить продукцию. Ожидаемый ежегодный доход (выручка) планируется в размере 3500 тыс. р. при ежегодных текущих затратах 1500 тыс. р. Инвестор считает, что учетная ставка Центрального банка РФ в период строительства предприятия будет равна 10 % годовых, а в период эксплуатации предприятия — 9 % годовых.
Какова целесообразность строительства предприятия?
Методические указания: 1) Оценить инвестиционный проект по всем возможным критериям с учетом и без учета дисконта денежных потоков; 2) Результаты расчета денежных потоков представить на графиках суммарной величины дисконтируемых и недисконтируемых денежных потоков в зависимости от времени.
Задача 14.Инвестор принял решение о строительстве предприятия, которое предполагается эксплуатировать 16 лет. Инвестиции, общей суммой 10 000 тыс. р., решено вкладывать поэтапно в начале каждого года строительства предприятия в течение 3 лет: в 1-й год — 4000 тыс. р.; во 2-й — 4000 тыс. р.; в 3-й — 2000 тыс. р. По окончании 3 лет строительства предприятие будет построено, введено в эксплуатацию и начнет производить продукцию, ожидаемый ежегодный доход (выручка) от которой намечается в размере 4000 тыс. р. при ежегодных текущих затратах 2000 тыс. р. Инвестор считает, что учетная ставка Центрального банка РФ в период строительства предприятия будет равна 10 % годовых, а в период эксплуатации предприятия — 8 % годовых.
Оценить эффективность принятого решения.
Методические указания: 1) Оценить инвестиционный проект по всем возможным критериям с учетом и без учета дисконта денежных потоков; 2) Результаты расчета денежных потоков представить на графиках суммарной величины дисконтируемых и недисконтируемых денежных потоков в зависимости от времени.
Задача 15.Имеется инвестиционный проект строительства предприятия, которое предполагается эксплуатировать 20 лет. Инвестиции, общей суммой 11 000 тыс. р., решено вкладывать поэтапно в начале каждого года строительства предприятия в течение 3 лет: в 1-й год — 5000 тыс. р.; во 2-й — 4000 тыс. р.; в 3-й — 2000 тыс. р. По окончании 3 лет строительства предприятие будет построено, введено в эксплуатацию и начнет производить продукцию, ожидаемый ежегодный доход (выручка) от которой намечается в размере 4000 тыс. р. при ежегодных текущих затратах 1500 тыс. р. Инвестор считает, что учетная ставка Центрального банка РФ в период строительства предприятия будет равна 11 % годовых, а в период эксплуатации предприятия — 10 % годовых.
Какова эффективность инвестиционного проекта?
Методические указания: 1) Оценить инвестиционный проект по всем возможным критериям с учетом и без учета дисконта денежных потоков; 2) Результаты расчета денежных потоков представить на графиках суммарной величины дисконтируемых и недисконтируемых денежных потоков в зависимости от времени.
Задача 16.Оценить эффективность инвестиций в строительство предприятия, которое предполагается эксплуатировать 20 лет. Инвестиции, общей суммой 10 000 тыс. р., решено вкладывать поэтапно в начале каждого года строительства предприятия в течение 3 лет: в 1-й год — 3000 тыс. р.; во 2-й — 2000 тыс. р.; в 3-й — 5000 тыс. р. По окончании 3 лет строительства предприятие будет построено, введено в эксплуатацию и начнет производить продукцию, ожидаемый ежегодный доход (выручка) от которой намечается в размере 5000 тыс. р. при ежегодных текущих затратах 3000 тыс. р. Инвестор считает, что учетная ставка Центрального банка РФ в период строительства предприятия будет равна 11 % годовых, а в период эксплуатации предприятия — 10 % годовых.
Методические указания: 1) Оценить инвестиционный проект по всем возможным критериям с учетом и без учета дисконта денежных потоков; 2) Результаты расчета денежных потоков представить на графиках суммарной величины дисконтируемых и недисконтируемых денежных потоков в зависимости от времени.
Задача 17.Инвестор должен принять решение о вложении денежных средств в строительство предприятия, которое предполагается эксплуатировать 18 лет. Инвестиции, общей суммой 10 000 тыс. р., решено вкладывать поэтапно в начале каждого года строительства предприятия в течение 3 лет: в 1-й год — 3000 тыс. р.; во 2-й — 3000 тыс. р.; в 3-й — 4000 тыс. р. По окончании 3 лет строительства предприятие будет построено, введено в эксплуатацию и начнет производить продукцию, ожидаемый ежегодный доход (выручка) от которой намечается в размере 4000 тыс. р. при ежегодных текущих затратах 2300 тыс. р. Инвестор считает, что учетная ставка Центрального банка РФ в период строительства предприятия будет равна 13 % годовых, а в период эксплуатации предприятия — 11 % годовых.
Что можно посоветовать инвестору?
Методические указания: 1) Оценить инвестиционный проект по всем возможным критериям с учетом и без учета дисконта денежных потоков; 2) Результаты расчета денежных потоков представить на графиках суммарной величины дисконтируемых и недисконтируемых денежных потоков в зависимости от времени.
Задача 18.Оценить приемлемость проекта строительства предприятия, которое предполагается эксплуатировать 25 лет. Инвестиции, общей суммой 10 000 тыс. р., решено вкладывать поэтапно в начале каждого года строительства предприятия в течение 3 лет: в 1-й год — 4000 тыс. р.; во 2-й — 3000 тыс. р.; в 3-й — 3000 тыс. р. По окончании 3 лет строительства предприятие будет построено, введено в эксплуатацию и начнет производить продукцию, ожидаемый ежегодный доход (выручка) от которой намечается в размере 3500 тыс. р. при ежегодных текущих затратах 1600 тыс. р. Инвестор считает, что учетная ставка Центрального банка РФ в период строительства предприятия будет равна 10 % годовых, а в период эксплуатации предприятия — 9 % годовых.
Методические указания: 1) Оценить инвестиционный проект по всем возможным критериям с учетом и без учета дисконта денежных потоков; 2) Результаты расчета денежных потоков представить на графиках суммарной величины дисконтируемых и недисконтируемых денежных потоков в зависимости от времени.
Задача 19.Реализация проекта строительства предприятия требует инвестиций общей суммой 12 000 тыс. р. Предприятие предполагается эксплуатировать 16 лет. Инвестиции осуществляются поэтапно в начале каждого года строительства предприятия в течение 3 лет: в 1-й год — 6000 тыс. р.; во 2-й — 4000 тыс. р.; в 3-й — 2000 тыс. р. По окончании 3 лет строительства предприятие будет построено, введено в эксплуатацию и начнет производить продукцию, ожидаемый ежегодный доход (выручка) от которой намечается в размере 4000 тыс. р. при ежегодных текущих затратах 2000 тыс. р. Инвестор считает, что учетная ставка Центрального банка РФ в период строительства предприятия будет равна 10 % годовых, а в период эксплуатации предприятия — 8 % годовых.
Какова целесообразность вложения инвестиций в строительство предприятия?
Методические указания: 1) Оценить инвестиционный проект по всем возможным критериям с учетом и без учета дисконта денежных потоков; 2) Результаты расчета денежных потоков представить на графиках суммарной величины дисконтируемых и недисконтируемых денежных потоков в зависимости от времени.
Метод дисконтирования денежных потоков
Методом дисконтирования денежных потоков инвесторы оценивают будущие ожидаемые денежные потоки и дисконтируют их по ставке доходности, которая учитывает временную стоимость денег и относительные риски инвестиций.
Можно представить метод дисконтирования денежных потоков следующей формулой:
DCF = CF1 / (1 k) CF2 / (1 k)2 CFn / (1 k)n,
где DCF — дисконтированный денежный поток;CF1, CF2, CFn — денежные потоки по периодам;k — ставка дисконтирования.
Свободный денежный поток компании представляет собой денежный поток от актива до выплаты каких-либо долговых платежей. В операционных денежных потоках не учитываются проценты и их влияние на налоги, так как этот фактор непосредственно учитывается в коэффициенте дисконтирования.
При оценке будущих ожидаемых денежных потоков обычно выделяют следующие типы рисков:
- единичный риск;
- рыночный риск.
- ставка дисконтирования для собственного капитала;
- ставка дисконтирования для заемного капитала.
- существует развитый высоколиквидный рынок акций;
- оценка финансового актива может осуществляться по прогнозируемым потокам платежей, получаемых владельцами капитала;
- дивиденды по акциям фиксированы и не меняются по годам;
- срок обращения акций не ограничен.
- для всех инвесторов период вложения одинаков;
- информация свободно и незамедлительно доступна для всех инвесторов;
- инвесторы имеют однородные ожидания, то есть одинаково оценивают будущие доходности, риск и ковариации доходностей ценных бумаг;
- безрисковая процентная ставка одинакова для всех инвесторов.
Единичный риск представляет собой неопределенности, присущие ожидаемым денежным потокам.
Метод оценки риска
Метод оценки риска — это использование метода статистической вероятности. При применении метода оценки по ожидаемой приведенной стоимости используется набор потоков денежных средств, который представляет взвешенное с учетом вероятности среднее значение всех возможных будущих потоков денежных средств. Получаемая в результате расчетная величина идентична ожидаемой стоимости, которая в статистическом выражении является средневзвешенным значением возможной стоимости дискретной случайной переменной с соответствующей взвешиваемой вероятностью. Поскольку все возможные потоки денежных средств взвешиваются с учетом вероятности, получаемый в результате ожидаемый поток денежных средств не является условным и не зависит от возникновения какого-либо определенного события.
Пример 6
Компания А рассчитывает справедливую стоимость оборудования. Стоимость капитала компании составляет 10 %. Имеется следующая информация о распределении вероятности поступления денежных потоков:

Рассчитаем дисконтированную стоимость денежных потоков.

В данном случае справедливая стоимость актива составит 24 693 тыс. руб.
Следует отметить, что на практике может существовать много возможных результатов (исходов). Однако для того чтобы применить метод оценки по ожидаемой приведенной стоимости, не всегда нужно учитывать распределение всех возможных потоков денежных средств, используя сложные модели и методы. Вместо этого можно разработать ограниченное количество дискретных сценариев и вероятностей, которые охватывают множество возможных потоков денежных средств.
Ставка дисконтирования
Приведение спрогнозированных денежных потоков в текущую стоимость осуществляется с помощью ставки дисконтирования.
Справочно
Ставка дисконтирования — это норма доходности, которую желает получать инвестор от вложенных средств. При этом важной составляющей нормы доходности является компенсация за риск, связанный с инвестированием.
Следует отметить, что ставка дисконтирования не зависит от структуры капитала компании и способа, с помощью которого компания финансировала приобретение актива, поскольку будущие потоки денежных средств, ожидаемые от актива, не зависят от того, каким образом компания финансировала приобретение актива. Применяемая ставка дисконтирования должна соответствовать типу денежного потока.
Ставки дисконтирования можно также подразделить следующим образом:
Взаимосвязь ставки дисконтирования для собственного капитала и ставки дисконтирования для заемного капитала характеризуется следующей формулой средневзвешенной стоимости капитала (WACC):
WACC = Ke × We Kp × Wp Kd × Wd × (1 × T),
где Ke — стоимость обыкновенных акций, %;
We — доля обыкновенных акций в структуре капитала;
Kp — стоимость привилегированных акций, %;
Wp — доля привилегированных акций в структуре капитала;
Kd — стоимость заемного капитала, %;
Wd — доля заемного капитала в структуре капитала;
T — ставка налога на прибыль, %.
Расчет стоимости собственного капитала ставки на основе модели дисконтирования дивидендов (kр) рассчитывается по следующей формуле:
kр = D / P,
где D — фиксированный размер выплачиваемых дивидендов;
Р — рыночная цена одной акции в настоящий момент.
Данный расчет основывается на следующих предположениях:
Расчет стоимости собственного капитала на основе модели стоимости обыкновенных акций (kе) с прогнозируемым приростом дивидендов основывается на формуле:
kе = (D1 / P0) g,
где D1 — денежные дивиденды на одну акцию, выплата которых ожидается в конце первого периода;
Р0 — рыночная цена одной акции в настоящий момент;
g — прогнозируемый ежегодный рост дивидендов.
Данный метод лучше всего подходит для компаний, растущих со скоростью, не превышающей скорости номинального роста в экономике, с хорошо установленной политикой выплаты дивидендов, и эти выплаты они намерены производить и в будущем.
Стоимость собственного капитала рассчитывается также на основе модели оценки капитальных активов (САРМ). Модель оценки капитальных активов предусматривает, что ожидаемая доходность инвестора складывается из двух компонентов: безрисковой ставки доходности и премии за риск инвестирования. Сама же премия за риск корректируется на систематический риск актива. Систематический риск обозначается бета-коэффициентом (β).
Важнейшие из предположений в данной модели:
Ниже представлена формула расчета стоимости собственного капитала (Re) по модели САРМ:
Re = Rf (Rm − Rf ) × β,
где Rf — безрисковая ставка доходности, %;
Rm — рыночная доходность собственного капитала, %;
(Rm − Rf) — премия за риск, %;
β — бета-коэффициент, характеризующий риск компании.
Считается, что безрисковая ставка доходности одинакова для всех инвесторов. В качестве безрисковой ставки могут использоваться государственные облигации страны-эмитента.
Метод CAPM является наиболее рыночным. При наличии развитого фондового рынка в оценочной практике данный метод применяется наиболее часто.
Таким образом, принцип временной стоимости денег используется в финансовом учете для отражения ряда операций, например связанных с учетом сделок по долгосрочным займам, финансовой аренде, кредиторской и дебиторской задолженности, с учетом операций с векселями и облигациями, для отражения амортизации премий и дисконтов (скидок) по облигациям, для оценки компонентов затрат и многого другого.
Принцип временной стоимости денег является основой в области финансов, он дает понимание ценности денег во времени, имеет решающее значение для определения ожидаемой отдачи от вложенных инвестиций.






