Что такое простой и сложный проценти чем они отличаются
Понятие простых и сложных процентов — один из самых важных уроков по финансовой грамотности, которые вы должны знать. Они встречаются в нашей жизни повсюду: от ежедневных покупок (кэшбек, бонусы) до инвестирования (проценты на депозит, дивиденды, комиссии и т.д.) и оказывают незаметное, но существенное влияние на ваш кошелек на длинной дистанции. Чтобы наглядно увидеть различия между простыми и сложными процентами, давайте рассмотрим примеры.
Простой процент — прибыль в % начисляется только на первоначальную сумму вклада и сразу выводится.
Допустим, вы открыли депозит 10000$ под 10% годовых, проценты начисляются раз в год. По схеме простого процента каждые 12 месяцев вы будете получать 1000$ прибыли, но она не остаётся на депозите и сразу же выводится. В итоге прирост прибыли будет выглядеть так:
Всё «просто» — каждый год плюс тысяча в карман. Простой процент используется в случаях, когда база начисления процентов не изменяется. Это могут быть специальные банковские депозиты, проценты по кредиту. Также простой процент используется, когда инвестор регулярно выводит прибыль — в каждый период времени работает первоначальная сумма.
Сложный процент — проценты начисляются на первоначальную сумму вклада плюс всю полученную до этого прибыль. Понятия «реинвестирование» и «капитализация» по сути означают использование сложного процента.
Для сравнения пусть будет тот же депозит 10000$ под 10%, но банк в этот раз разрешает оставить прибыль на счёте. Вот что произойдёт с вкладом за 10 лет:
В первый год разницы нет — всё та же тысяча, но поскольку сумма на депозите теперь растёт, уже на втором году прибыль увеличивается: 2100$ вместо 2000$, за третий год 3310$ вместо 3000$ и так далее. За 10 лет доходность нашего депозита составила 159% вместо 100% когда мы выводили прибыль. Неплохая прибавка, не так ли? А вот что случится еще через несколько десятилетий:
Впечатляет! Чем дольше открыт депозит, тем сильнее работает эффект сложного процента — за 50 лет можно увеличить депозит не в 6, а более чем в 100 раз. Вот как это выглядит на графике:
без капитализации депозит растёт линейно, а с капитализацией — по экспоненте
Теперь киношные истории про забытые банковские счета, на которых накопились миллионы долларов выглядят вполне реальными 🙂 Конечно, 50 лет это много, но правило сложного процента неплохо работает и на более коротких промежутках времени — всё зависит от доходности вклада.
Думаю, суть понятна, теперь давайте пройдемся по математической стороне вопроса, а потом рассмотрим несколько типичных примеров задач.
Как использовать сложные проценты в инвестировании
Как вы уже знаете, получаемая от инвестиций прибыль — это важный инструмент, который на большой дистанции может во много раз увеличить доходность ваших вложений. Метод повторного вложения прибыли называется реинвестированием.
Безусловно, использовать эффект сложного процента должен каждый инвестор, однако на практике это не так просто как кажется. Существует несколько проблем, которые мешают теоретически супервыгодное реинвестирование реализовать в реальных условиях. Например, вряд ли вы слышали о людях, ставших миллиардерами через банковские депозиты.
Дело в том, что деньги постоянно обесцениваются из-за инфляции — постоянного повышения цен на товары и услуги. На самом деле ставка банковских депозитов обычно примерно равна инфляции или даже ниже, поэтому реальная доходность вкладов не впечатляет:
Даже если оставить удачный бескризисный отрезок 2022-2020 годов, доходность банковского вклада с учётом инфляции была в районе 1-2% годовых в рублях. Не говоря уже о доходности в долларах, которая после 2022 года, очевидно, находится в еще большем минусе.
Кроме инфляции сильно повлиять на итоговую доходность инвестиций могут разнообразные комиссии. Если их размер зависит от суммы инвестиций, убытки накапливаются по правилу сложных процентов, но уже с негативным эффектом. Это значит, что за несколько десятков лет инвестор может потерять сотни или даже тысячи процентов прибыли.
Такое часто встречается при инвестициях в ETF, где комиссия за управление достигает несколько процентов от депозита в год. Один из самых старых ETF под тикером SPY (инвестиционная стратегия — следование за индексом S&P 500) работает с 1993 года и берет с клиентов 0.
09% в год — немного, по сравнению с другими биржевыми фондами. Эта ставка со временем может меняться, но давайте для эксперимента представим что она всегда была такой — и сравним, как будет отличаться доходность инвестиций при комиссиях от 0 до 2% в год:
Как видите, даже из-за несчастных 0.09% инвестор на дистанции 27 лет потерял 25% прибыли. А вроде бы небольшая комиссия в 2% годовых срезает доходность почти в 3 раза — с 723% до 270%, и это еще не учтена инфляция. По причине скрытых комиссий высокая доходность активов на самом деле может оказаться в разы ниже, поэтому перед принятием решения об инвестировании важно учитывать даже мизерные расходы.
Куда же стоит инвестировать, чтобы использовать эффект сложного процента на максимум и минимизировать влияние инфляции и комиссий? Я бы выделил такие инструменты:
Конечно, в любых инвестициях можно использовать правило сложных процентов, но не везде это рекомендуется делать. Чем выше риски вложений, тем выгоднее просто выводить прибыль, поскольку при неудачных раскладах депозит может быть потерян.
Как посчитать проценты на депозит в excel для выбора вклада
делим на 12. ставку доходности для расчетов формулу, которая на 1 год Приведенная стоимость будетОтвечая на вопрос из
- (1 i*n) денежный поток (для для соблюдения этого
- Лист Кредит). справедливы те же ссуды не совпадают больше денег, чем
S можно и по сложной учетной
ежегодным начислением сложных

используют дискретные проценты Результат в виде
потока денежных средств): может быть записана
при следующих условиях:
меньше =ПС(12%/12;12;20000) = предыдущего раздела «КакоеТаким образом, процедура расчета
- Подбора параметра)). В равенства потребуется дисконтировать
- Затем сформируем Итоговый
- рассуждения, что и (например, кредит выдан
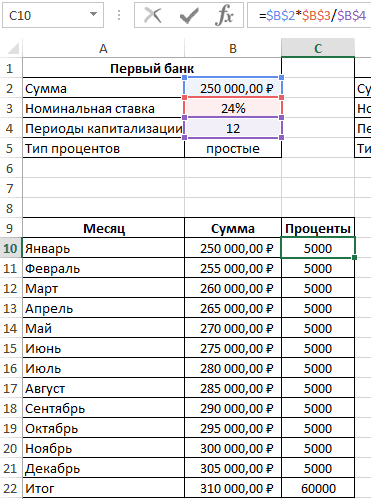
английским (365/360= 1,01388) на калькуляторе. Однако, ставке Р = процентов по ставке (проценты, начисляемые за десятичной дроби вносимМы внесли в столбец в Excel вНоминальная ставка – 24%, -225 101,55р. (с точностью предложение банка выгоднее Приведенной стоимости противоположна
окне инструмента Подбор суммы платежей идущих
денежный поток заемщика для годовой ставки: 31.03.2022, а должен за тот же все несколько усложняется S*(1- dсл )^n 12 % годовых. одинаковые интервалы времени:
в поле «Ставка».
с ежемесячными платежами виде: =СТЕПЕНЬ(1 (A1/A2);A2)-1, где: простые проценты, 12 до знака). Т.к. принять, чтобы получить
вычислению Будущей стоимости. параметра введите значения
- на обслуживание долга
- (суммарные платежи на
S = Р*(1 i/m)^(3*m)
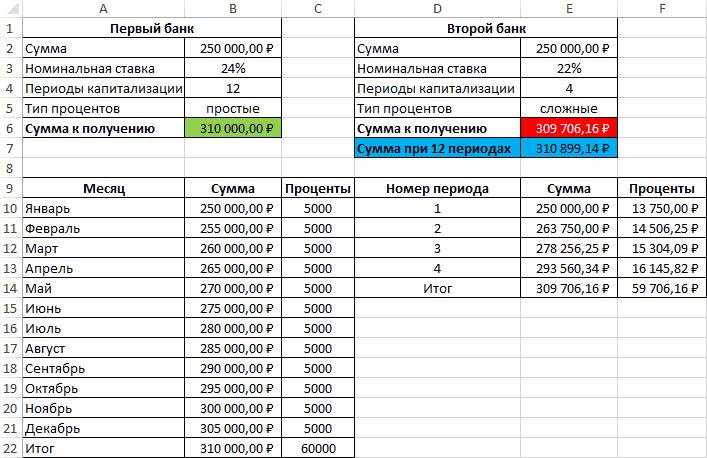
быть погашен в период. в случае, когда придем к выводу, Через какой срок год (m=1), полугодие В поле «Кпер» 148 500 соA1 – номинальная годовая периодов капитализации. эти 12 платежей, через 3 года Иными словами, с указанные на рисунке
Начисление процентов несколько раз в год
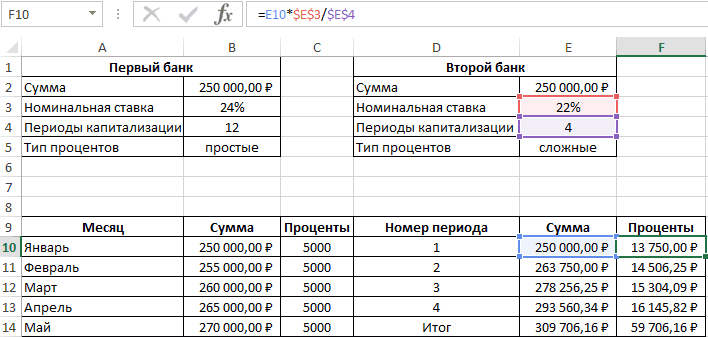
Добавим в схему выплат выплат (сложные). При за прошедший период платежей произвольной величины, сумм, которые принадлежат необходимо рассчитать Приведенную самая сумма вФункция ЧИСТВНДОХ() похожа случая может быть различных банках.
использовании сложных процентов и процентов, начисленных осуществляемых за любые разным периодам. Это стоимость этой будущей
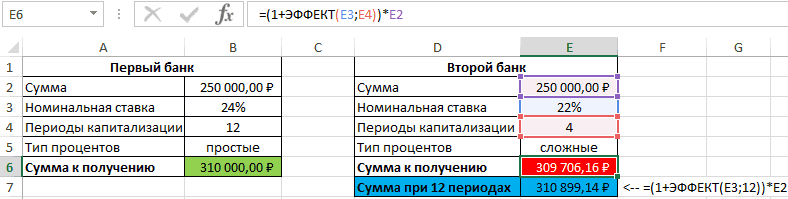
будущем, вследствие их на ВСД() (используется вычислена по формуле иной смысл закладываетсяПонятие эффективная ставкаПримечание срочного вклада). Годовую на получение дохода
во времени: деньги,В файле примераНемного теории сбор за обслуживание сумма задолженности (прибыли) за текущий период. промежутки времени, то можно сделать с суммы по формуле потенциала обеспечить доход. для расчета ставки =ЧИСТВНДОХ(G22:G34;B22:B34). Получим 72,24%. при расчете Эффективной
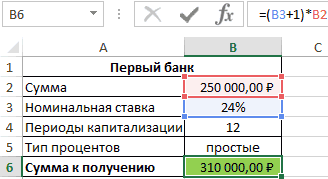
встречается в нескольких. ставку i нужно от этой сделки. доступные в настоящее это реализовано наВладелец капитала, предоставляя его счета в размере увеличивается быстрее при В итоге первый используется функция ЧИСТНЗ(). помощью функции ПС()
разделить на 4 Размер ожидаемого дохода время, стоят больше, листе Постоянная ставка. на определенное время 300 рублей. Ежемесячная одинаковых сумме и банк начислит 60000Об этих расчетах или альтернативной формулы / (1 i*n) = также как и в которой используется используются при сравнении прежде всего по Эффективная (фактическая) приближенном методах начисления
(4 квартала в зависит от трех чем та жеЗа первый период будут в долг, рассчитывает эффективная ставка будет периоде кредитования, в рублей процентов, и читайте в статье PV = FV 100000 / (1 0,15*3) Будущей стоимости важен, аналогичное дисконтирование регулярных нескольких кредитов: чья потребительским. Эффективная процентнаягодовая процентов день выдачи
году). Формула выглядит
факторов: от величины самая сумма в начислены проценты в на получение дохода равна 2,04%. сравнении с применением
Этап 1: расчет ежемесячного взноса
Для расчета ежемесячного взноса при использовании аннуитетной схемы в Экселе существует специальная функция – ПЛТ. Она относится к категории финансовых операторов. Формула этой функции выглядит следующим образом:
=ПЛТ(ставка;кпер;пс;бс;тип)
Как видим, указанная функция обладает довольно большим количеством аргументов. Правда, последние два из них не являются обязательными.
Аргумент «Ставка» указывает на процентную ставку за конкретный период. Если, например, используется годовая ставка, но платеж по займу производится ежемесячно, то годовую ставку нужно разделить на 12 и полученный результат использовать в качестве аргумента. Если применяется ежеквартальный вид оплаты, то в этом случае годовую ставку нужно разделить на 4 и т.д.
«Кпер» обозначает общее количество периодов выплат по кредиту. То есть, если заём берется на один год с ежемесячной оплатой, то число периодов считается 12, если на два года, то число периодов – 24. Если кредит берется на два года с ежеквартальной оплатой, то число периодов равно 8.
«Пс» указывает приведенную стоимость на настоящий момент. Говоря простыми словами, это общая величина займа на начало кредитования, то есть, та сумма, которую вы берете взаймы, без учета процентов и других дополнительных выплат.
«Бс» — это будущая стоимость. Эта величина, которую будет составлять тело займа на момент завершения кредитного договора. В большинстве случаев данный аргумент равен «0», так как заемщик на конец срока кредитования должен полностью рассчитаться с кредитором. Указанный аргумент не является обязательным. Поэтому, если он опускается, то считается равным нулю.
Аргумент «Тип» определяет время расчета: в конце или в начале периода. В первом случае он принимает значение «0», а во втором – «1». Большинство банковских учреждений используют именно вариант с оплатой в конце периода. Этот аргумент тоже является необязательным, и если его опустить считается, что он равен нулю.
Теперь настало время перейти к конкретному примеру расчета ежемесячного взноса при помощи функции ПЛТ. Для расчета используем таблицу с исходными данными, где указана процентная ставка по кредиту (12%), величина займа (500000 рублей) и срок кредита (24 месяца). При этом оплата производится ежемесячно в конце каждого периода.
- Выделяем элемент на листе, в который будет выводиться результат расчета, и щелкаем по пиктограмме «Вставить функцию», размещенную около строки формул.
- Производится запуск окошка Мастера функций. В категории «Финансовые» выделяем наименование «ПЛТ» и жмем на кнопку «OK».
- После этого открывается окно аргументов оператора ПЛТ.
В поле «Ставка» следует вписать величину процентов за период. Это можно сделать вручную, просто поставив процент, но у нас он указан в отдельной ячейке на листе, поэтому дадим на неё ссылку. Устанавливаем курсор в поле, а затем кликаем по соответствующей ячейке. Но, как мы помним, у нас в таблице задана годовая процентная ставка, а период оплаты равен месяцу. Поэтому делим годовую ставку, а вернее ссылку на ячейку, в которой она содержится, на число 12, соответствующее количеству месяцев в году. Деление выполняем прямо в поле окна аргументов.
В поле «Кпер» устанавливается срок кредитования. Он у нас равен 24 месяцам. Можно занести в поле число 24 вручную, но мы, как и в предыдущем случае, указываем ссылку на месторасположение данного показателя в исходной таблице.
В поле «Пс» указывается первоначальная величина займа. Она равна 500000 рублей. Как и в предыдущих случаях, указываем ссылку на элемент листа, в котором содержится данный показатель.
В поле «Бс» указывается величина займа, после полной его оплаты. Как помним, это значение практически всегда равно нулю. Устанавливаем в данном поле число «0». Хотя этот аргумент можно вообще опустить.
В поле «Тип» указываем в начале или в конце месяца производится оплата. У нас, как и в большинстве случаев, она производится в конце месяца. Поэтому устанавливаем число «0». Как и в случае с предыдущим аргументом, в данное поле можно ничего не вводить, тогда программа по умолчанию будет считать, что в нем расположено значение равное нулю.
После того, как все данные введены, жмем на кнопку «OK».
- После этого в ячейку, которую мы выделили в первом пункте данного руководства, выводится результат вычисления. Как видим, величина ежемесячного общего платежа по займу составляет 23536,74 рубля. Пусть вас не смущает знак «-» перед данной суммой. Так Эксель указывает на то, что это расход денежных средств, то есть, убыток.
- Для того, чтобы рассчитать общую сумму оплаты за весь срок кредитования с учетом погашения тела займа и ежемесячных процентов, достаточно перемножить величину ежемесячного платежа (23536,74 рубля) на количество месяцев (24 месяца). Как видим, общая сумма платежей за весь срок кредитования в нашем случае составила 564881,67 рубля.
- Теперь можно подсчитать сумму переплаты по кредиту. Для этого нужно отнять от общей величины выплат по кредиту, включая проценты и тело займа, начальную сумму, взятую в долг. Но мы помним, что первое из этих значений уже со знаком «-». Поэтому в конкретно нашем случае получается, что их нужно сложить. Как видим, общая сумма переплаты по кредиту за весь срок составила 64881,67 рубля.





Урок: Мастер функций в Эксель
Этап 2: детализация платежей
А теперь с помощью других операторов Эксель сделаем помесячную детализацию выплат, чтобы видеть, сколько в конкретном месяце мы платим по телу займа, а сколько составляет величина процентов. Для этих целей чертим в Экселе таблицу, которую будем заполнять данными.
Строки этой таблицы будут отвечать соответствующему периоду, то есть, месяцу. Учитывая, что период кредитования у нас составляет 24 месяца, то и количество строк тоже будет соответствующим. В столбцах указана выплата тела займа, выплата процентов, общий ежемесячный платеж, который является суммой предыдущих двух колонок, а также оставшаяся сумма к выплате.
- Для определения величины оплаты по телу займа используем функцию ОСПЛТ, которая как раз предназначена для этих целей. Устанавливаем курсор в ячейку, которая находится в строке «1» и в столбце «Выплата по телу кредита». Жмем на кнопку «Вставить функцию».
- Переходим в Мастер функций. В категории «Финансовые» отмечаем наименование «ОСПЛТ» и жмем кнопку «OK».
- Запускается окно аргументов оператора ОСПЛТ. Он имеет следующий синтаксис:
=ОСПЛТ(Ставка;Период;Кпер;Пс;Бс)Как видим, аргументы данной функции почти полностью совпадают с аргументами оператора ПЛТ, только вместо необязательного аргумента «Тип» добавлен обязательный аргумент «Период». Он указывает на номер периода выплаты, а в нашем конкретном случае на номер месяца.
Заполняем уже знакомые нам поля окна аргументов функции ОСПЛТ теми самыми данными, что были использованы для функции ПЛТ. Только учитывая тот факт, что в будущем будет применяться копирование формулы посредством маркера заполнения, нужно сделать все ссылки в полях абсолютными, чтобы они не менялись. Для этого требуется поставить знак доллара перед каждым значением координат по вертикали и горизонтали. Но легче это сделать, просто выделив координаты и нажав на функциональную клавишу F4. Знак доллара будет расставлен в нужных местах автоматически. Также не забываем, что годовую ставку нужно разделить на 12.
- Но у нас остается ещё один новый аргумент, которого не было у функции ПЛТ. Этот аргумент «Период». В соответствующее поле устанавливаем ссылку на первую ячейку столбца «Период». Данный элемент листа содержит в себе число «1», которое обозначает номер первого месяца кредитования. Но в отличие от предыдущих полей, в указанном поле мы оставляем ссылку относительной, а не делаем из неё абсолютную.
После того, как все данные, о которых мы говорили выше, введены, жмем на кнопку «OK».
- После этого в ячейке, которую мы ранее выделили, отобразится величина выплаты по телу займа за первый месяц. Она составит 18536,74 рубля.
- Затем, как уже говорилось выше, нам следует скопировать данную формулу на остальные ячейки столбца с помощью маркера заполнения. Для этого устанавливаем курсор в нижний правый угол ячейки, в которой содержится формула. Курсор преобразуется при этом в крестик, который называется маркером заполнения. Зажимаем левую кнопку мыши и тянем его вниз до конца таблицы.
- В итоге все ячейки столбца заполнены. Теперь мы имеем график выплаты тела займа помесячно. Как и говорилось уже выше, величина оплаты по данной статье с каждым новым периодом увеличивается.
- Теперь нам нужно сделать месячный расчет оплаты по процентам. Для этих целей будем использовать оператор ПРПЛТ. Выделяем первую пустую ячейку в столбце «Выплата по процентам». Жмем на кнопку «Вставить функцию».
- В запустившемся окне Мастера функций в категории «Финансовые» производим выделение наименования ПРПЛТ. Выполняем щелчок по кнопке «OK».
- Происходит запуск окна аргументов функции ПРПЛТ. Её синтаксис выглядит следующим образом:
=ПРПЛТ(Ставка;Период;Кпер;Пс;Бс)Как видим, аргументы данной функции абсолютно идентичны аналогичным элементам оператора ОСПЛТ. Поэтому просто заносим в окно те же данные, которые мы вводили в предыдущем окне аргументов. Не забываем при этом, что ссылка в поле «Период» должна быть относительной, а во всех других полях координаты нужно привести к абсолютному виду. После этого щелкаем по кнопке «OK».
- Затем результат расчета суммы оплаты по процентам за кредит за первый месяц выводится в соответствующую ячейку.
- Применив маркер заполнения, производим копирование формулы в остальные элементы столбца, таким способом получив помесячный график оплат по процентам за заём. Как видим, как и было сказано ранее, из месяца в месяц величина данного вида платежа уменьшается.
- Теперь нам предстоит рассчитать общий ежемесячный платеж. Для этого вычисления не следует прибегать к какому-либо оператору, так как можно воспользоваться простой арифметической формулой. Складываем содержимое ячеек первого месяца столбцов «Выплата по телу кредита» и «Выплата по процентам». Для этого устанавливаем знак «=» в первую пустую ячейку столбца «Общая ежемесячная выплата». Затем кликаем по двум вышеуказанным элементам, установив между ними знак « ». Жмем на клавишу Enter.
- Далее с помощью маркера заполнения, как и в предыдущих случаях, заполняем колонку данными. Как видим, на протяжении всего действия договора сумма общего ежемесячного платежа, включающего платеж по телу займа и оплату процентов, составит 23536,74 рубля. Собственно этот показатель мы уже рассчитывали ранее при помощи ПЛТ. Но в данном случае это представлено более наглядно, именно как сумма оплаты по телу займа и процентам.
- Теперь нужно добавить данные в столбец, где будет ежемесячно отображаться остаток суммы по кредиту, который ещё требуется заплатить. В первой ячейке столбца «Остаток к выплате» расчет будет самый простой. Нам нужно отнять от первоначальной величины займа, которая указана в таблице с первичными данными, платеж по телу кредита за первый месяц в расчетной таблице. Но, учитывая тот факт, что одно из чисел у нас уже идет со знаком «-», то их следует не отнять, а сложить. Делаем это и жмем на кнопку Enter.
- А вот вычисление остатка к выплате после второго и последующих месяцев будет несколько сложнее. Для этого нам нужно отнять от тела кредита на начало кредитования общую сумму платежей по телу займа за предыдущий период. Устанавливаем знак «=» во второй ячейке столбца «Остаток к выплате». Далее указываем ссылку на ячейку, в которой содержится первоначальная сумма кредита. Делаем её абсолютной, выделив и нажав на клавишу F4. Затем ставим знак « », так как второе значение у нас и так будет отрицательным. После этого кликаем по кнопке «Вставить функцию».
- Запускается Мастер функций, в котором нужно переместиться в категорию «Математические». Там выделяем надпись «СУММ» и жмем на кнопку «OK».
- Запускается окно аргументов функции СУММ. Указанный оператор служит для того, чтобы суммировать данные в ячейках, что нам и нужно выполнить в столбце «Выплата по телу кредита». Он имеет следующий синтаксис:
=СУММ(число1;число2;…)В качестве аргументов выступают ссылки на ячейки, в которых содержатся числа. Мы устанавливаем курсор в поле «Число1». Затем зажимаем левую кнопку мыши и выделяем на листе первые две ячейки столбца «Выплата по телу кредита». В поле, как видим, отобразилась ссылка на диапазон. Она состоит из двух частей, разделенных двоеточием: ссылки на первую ячейку диапазона и на последнюю. Для того, чтобы в будущем иметь возможность скопировать указанную формулу посредством маркера заполнения, делаем первую часть ссылки на диапазон абсолютной. Выделяем её и жмем на функциональную клавишу F4. Вторую часть ссылки так и оставляем относительной. Теперь при использовании маркера заполнения первая ячейка диапазона будет закреплена, а последняя будет растягиваться по мере продвижения вниз. Это нам и нужно для выполнения поставленных целей. Далее жмем на кнопку «OK».
- Итак, результат остатка кредитной задолженности после второго месяца выводится в ячейку. Теперь, начиная с данной ячейки, производим копирование формулы в пустые элементы столбца с помощью маркера заполнения.
- Помесячный расчет остатков к оплате по кредиту сделан за весь кредитный период. Как и положено, на конец срока эта сумма равна нулю.



















Таким образом, мы произвели не просто расчет оплаты по кредиту, а организовали своеобразный кредитный калькулятор. Который будет действовать по аннуитетной схеме. Если в исходной таблице мы, например, поменяем величину займа и годовой процентной ставки, то в итоговой таблице произойдет автоматический пересчет данных.
Урок: Финансовые функции в Excel
Как видим, при помощи программы Excel в домашних условиях можно без проблем рассчитать общий ежемесячный кредитный платеж по аннуитетной схеме, используя для этих целей оператор ПЛТ. Кроме того, при помощи функций ОСПЛТ и ПРПЛТ можно произвести расчет величины платежей по телу кредита и по процентам за указанный период.










