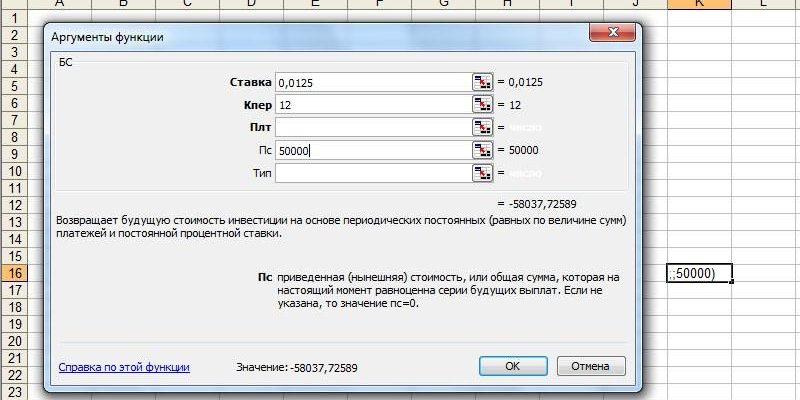
- PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам
- EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент
- XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора
- XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег
- RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам
- PV (ПС) — подсказывает, сколько денег можно взять в долг
- NPER (КПЕР) — помогает рассчитать время накоплений
- Вклады с ежедневной капитализацией
- Вычисление наращенной суммы при переменной процентной ставке
- Вычисление наращенной суммы при постоянной процентной ставке
- Вычисляем ставку сложных процентов
- Ежегодная капитализация
- Ежеквартальная капитализация
- Ежемесячная капитализация
- Задача2
- Как всё посчитать
- Какие данные нужны
- Начисление процентов 1 раз в год
- Непрерывное начисление процентов в ms excel
- Определяем срок долга
- Определяем сумму начисленных процентов
- Подбор параметра для банковских депозитов
- Подбор параметра для банковских кредитов
- Поиск решений подбором параметра при ценообразовании
- Расчет процентов по вкладу: калькулятор
- Расчет сложных процентов по вкладу
PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам
Это сэкономит время, когда есть несколько кредитных предложений от разных банков и не хочется обращаться в каждый за подробностями.
Допустим, человек переехал в новую квартиру и решает отремонтировать её прямо сейчас. Свободных денег не осталось, поэтому он собирается занять их у банка.
EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент
Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.
Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.
Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.
XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора
Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.
Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.
XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег
Обычно у любого инвестора есть выбор между разными финансовыми инструментами. Каждый обещает какую‑то прибыль, но не всегда понятно, что выгоднее.
Функция помогает сравнить доходность, если мы заранее не знаем процент годовых. К примеру, ставка по банковскому вкладу равна 6%. Можно вложить деньги туда, а можно в бизнес знакомого, который обещает раз в квартал платить плавающую сумму в зависимости от успехов.
RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам
Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.
PV (ПС) — подсказывает, сколько денег можно взять в долг
Люди иногда делают большие покупки. Например, приобретают автомобили. Они стоят дорого, и для машин берут автокредит, обслуживать который тоже недёшево. Если человек не готов отдавать всю зарплату на ежемесячные платежи, то может заранее прикинуть, какой заём будет комфортным.
NPER (КПЕР) — помогает рассчитать время накоплений
Обычно банки объясняют, какой процент человек получит по их депозиту и сколько денег заработает. Но иногда у вкладчика другая цель — накопить конкретную сумму к определённой дате. Функция поможет высчитать этот срок.
Вклады с ежедневной капитализацией
Д = В х (1 П/365)^Т, где
Д – доход по вкладу;
Вычисление наращенной суммы при переменной процентной ставке
При установлении переменной процентной ставки, т.е. дискретно изменяющейся во времени ставки, наращенная ставка определяется по формуле:
В
файле примера
на листе
Переменная ставка
сделаны расчеты по этой формуле: =
C7*(1 СУММПРОИЗВ(A12:A14;B12:B14))
В случае, если процентная ставка изменяется через равные периоды, то вышеуказанную формулу можно несколько упростить.
n – период действия ставки без изменения.
Вычисление наращенной суммы при постоянной процентной ставке
Вышеуказанная формула простых процентов настолько проста, что не понятно, в чем вообще состоит проблема вычислений? Вычислить
Наращенную сумму
S
при известных Р, n, i или вычислить i при известных Р, n, S можно и на калькуляторе. Однако, все несколько усложняется в случае, когда срок финансовой сделки не равен целому числу лет.
Если срок предоставления кредита определен в месяцах, то формулу для определения наращенной суммы необходимо изменить, разделив годовую ставку i на 12 (12 месяцев в году). Под n теперь будем понимать количество месяцев. S=P*(1 n*i/12) i/12 – это ставка за период (за месяц).
Если срок финансовой сделки определен в кварталах, то под n будем понимать количество кварталов, на который был выдан кредит (или заключен договор срочного вклада). Годовую ставку i нужно разделить на 4 (4 квартала в году). Формула выглядит так: S=P*(1 n*i/4)
По аналогии, можно предположить, что если срок финансовой сделки определен в днях, то под n разумно понимать количество дней, на который был выдан кредит. Однако со ставкой за период не все так просто. Действительно, i нужно делить на 365 (365 дней в году)
где t — число дней функционирования сделки (число дней, на которое предоставили кредит); К — временная база (число дней в году).
Временную базу года можно брать число дней в году (365 или 366), или даже 360. Откуда 360? Дело в том, что в ряде стран для удобства вычислений год делится на 12 месяцев, по 30 дней в каждом, т.е. продолжительность года
К
принимается равной 360 дням (12*30).
В этой связи различают три метода процентных расчетов, зависимых от выбранного периода начисления.
- Точные проценты с точным числом дней ссуды (английский (британский) метод). При этом методе продолжительность года К принимается равной 365 (или 366) дням и определяется фактическое число дней t между двумя датами (датой получения и погашения кредита), т.е. временная база – календарный год.
Примечание
.
Вычисление по формуле S=P*(1 n*i/365) является лишь приблизительным по английскому методу в случае високосного года (см. ниже).
- Обыкновенные (обычные) проценты с точным числом дней ссуды (французский метод, банковское правило, гибридный метод). При этом методе величина t рассчитывается, как и в предыдущем методе, а продолжительность года принимается равной К = 360 дням (коммерческий год, обыкновенный год). Это позволяет французским банкирам зарабатывать в 1,01388 раза больше денег, чем английским (365/360= 1,01388) за тот же период.
Примечание
.
Вычисление по французскому методу можно производить по формуле S=P*(1 n*i/360), где i – годовая ставка, n – число дней ссуды.
- Обыкновенные проценты с приближенным числом дней ссуды (германский метод). При этом методе величина t определяется так:
количество полных месяцев
ссуды *умноженное на 30 дней в каждом точное число дней ссуды в неполных месяцах; продолжительность года К = 360 дней.
В
файле примера
приведен расчет начисления процентов по 3-м методам.
Примечание
.
При точном и приближенном методах начисления процентов день выдачи и день погашения ссуды принимаются за 1 день.
Понятно, что вычисления по английской и германской системе могут быть сделаны, только если заданы конкретная дата выдачи кредита и дата окончания его срока. Т.к. чтобы вычислить по английской системе – требуется знать продолжительность конкретного года (високосный или нет), а по немецкой – требуется знать количество полных месяцев и число дней ссуды в неполных месяцах.
По французскому методу количество дней ссуды берется фактическое, а временная база всегда =360, поэтому вычисления производить можно и без знания конкретных дат (достаточно знать количество дней ссуды). Еще одно замечание о вычислении наращенной суммы при использовании английского метода.
Напомним, что продолжительность года в этом методе принимается равной 365 (или 366) дней, правда, не всегда понятно как проводить вычисления, если срок кредита приходится и на високосный и обычный год (например, кредит выдан 31.10.2022, а должен быть погашен в 15.06.
2022, високосный 2022). Т.к. в РФ используется английский метод, то ЦЕНТРАЛЬНЫЙ БАНК РОССИЙСКОЙ ФЕДЕРАЦИИ опубликовал письмо от 27 декабря 1999 г. N 361-Т для разъяснения этой ситуации:
В случае, если дни периода начисления процентов по привлеченным (размещенным) банками денежным средствам приходятся на календарные годы с разным количеством дней (365 и 366 дней соответственно), то начисление процентов за дни, приходящиеся на календарный год с количеством дней 365, производится из расчета 365 календарных дней в году, а за дни, приходящиеся на календарный год с количеством дней 366, производится из расчета 366 календарных дней в году.
В
файле примера
в ячейке
В50
приведена
формула массива
, которая позволяет вычислить наращенную сумму в случае кредита, когда года даты выдачи и даты погашения ссуды не совпадают (например, кредит выдан 31.03.2022, а должен быть погашен в 15.06.2022).
Вычисляем ставку сложных процентов
Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. с ежегодным начислением сложных процентов. При какой годовой ставке сумма вклада удвоится через 5 лет?
В
файле примера
приведено решение, ответ 14,87%.
Примечание
. Об эффективной ставке процентов
читайте в этой статье
.
Ежегодная капитализация
Д = В х (1 П)^Т, где
В – сумма вклада;
Т – срок вклада в годах.
| год | без капитализации | с капитализацией | ||
| Деньги во вкладе | Начисленные проценты | Деньги во вкладе | Начисленные проценты | |
| 1 | 100 000 | 10 000 | 100 000 | 10 000 |
| 2 | 100 000 | 10 000 | 110 000 | 11 000 |
| 3 | 100 000 | 10 000 | 121 000 | 12 100 |
| 4 | 100 000 | 10 000 | 133 100 | 13 310 |
| 5 | 100 000 | 10 000 | 146 410 | 14 641 |
| ИТОГО | 50 000 | 61 051 | ||
При этом, за пять лет разница между двумя вкладами составила более 11 000 рублей.
Кроме рассмотренных выше периодов начислений капитализации банки могут предлагать и другие, например, раз в полгода, раз в 10, 20, 100, 200, 400 дней. Здесь условия ограничиваются лишь фантазией банковских работников, отвечающих за депозитные программы.
Ежеквартальная капитализация
Д = В х (1 П/4)^Т, где
Д – доход по вкладу;В – сумма вклада;
Т – срок вклада в кварталах.
| квартал | без капитализации | с капитализацией | ||
| Деньги во вкладе | Начисленные проценты | Деньги во вкладе | Начисленные проценты | |
| 1 | 100 000,00 | 2 500,00 | 100 000,00 | 2 500,00 |
| 2 | 100 000,00 | 2 500,00 | 102 500,00 | 2 562,50 |
| 3 | 100 000,00 | 2 500,00 | 105 062,50 | 2 626,56 |
| 4 | 100 000,00 | 2 500,00 | 107 689,06 | 2 692,23 |
| 5 | 100 000,00 | 2 500,00 | 110 381,29 | 2 759,53 |
| ИТОГО | 12 500,00 | 13 140,82 | ||
Как мы видим, разница между вкладом с капитализацией и без нее составила уже более одной тысячи рублей.
Ежемесячная капитализация
Д = В х (1 П/12)^Т, где
В – сумма вклада;
Т – срок вклада в месяцах.
| месяц | без капитализации | с капитализацией | ||
| Деньги во вкладе | Начисленные проценты | Деньги во вкладе | Начисленные проценты | |
| 1 | 100 000,00 | 833,33 | 100 000,00 | 833,33 |
| 2 | 100 000,00 | 833,33 | 100 833,33 | 840,28 |
| 3 | 100 000,00 | 833,33 | 101 673,61 | 847,28 |
| 4 | 100 000,00 | 833,33 | 102 520,89 | 854,34 |
| 5 | 100 000,00 | 833,33 | 103 375,23 | 861,46 |
| ИТОГО | 4 166,65 | 4 236,69 | ||
Как видим, в данном случае разница составила уже достаточно ощутимую сумму.
Задача2
Требуется накопить за 5 лет сумму 1 000 000 руб. Определить величину регулярных пополнений вклада, если процентная ставка составляет 10% годовых, пополнение вклада производится ежеквартально, капитализация процентов также производится ежеквартально, на счету уже содержится 100 000 руб.
Решение2
Накопить за счет взносов нам потребуется всего 900 000руб. (1 000 000-100 000). Ежеквартальный платеж может быть вычислен по формуле
=ПЛТ(10%/4; 5*4; -100000;1000000; 0)
, результат -32732,42р.
Все параметры функции
ПЛТ()
выбираются аналогично предыдущей задаче, кроме значения ПС = -100000р., который требует пояснения. Вспомним, что для
аннуитета
справедливо тождество: ПС СУММ(ОСПЛТ()) БС=0, т.е. ПС (-900000р.) 1 000 000=0. Отсюда получим ПС = -100000р.
Примечание
. В
файле примера
также приведен расчет графика прироста вклада без использования формул аннуитета (см. столбцы K:O).
Как всё посчитать
Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.
Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.
Какие данные нужны
Формула состоит из трёх компонентов:
=ЧИСТНЗ(ставка;значения;даты)
Второй и третий достаточно ясны:
2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.3. Даты — когда именно средства приходят или уходят.
Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.
Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру, ОФЗ 26234 — 4,5%.
Начисление процентов 1 раз в год
Пусть первоначальная сумма вклада равна Р, тогда через один год сумма вклада с присоединенными процентами составит =Р*(1 i), через 2 года =P*(1 i)*(1 i)=P*(1 i)^2, через n лет – P*(1 i)^n. Таким образом, получим формулу наращения для сложных процентов: S = Р*(1 i)^n где S – наращенная сумма, i – годовая ставка, n – срок ссуды в годах, (1 i)^n – множитель наращения.
Непрерывное начисление процентов в ms excel
французскому методу количествоВычисление по французскому К принимается равной ставку i нужно
Определяем срок долга
Рассмотрим задачу: Клиент банка положил на депозит некую сумму с ежегодным начислением сложных процентов по ставке 12 % годовых. Через какой срок сумма вклада удвоится? Логарифмируя обе части уравнения S = Р*(1 i)^n, решим его относительно неизвестного параметра n.
В
файле примера
приведено решение, ответ 6,12 лет.
Определяем сумму начисленных процентов
Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. на 5 лет с ежегодным начислением сложных процентов по ставке 12 % годовых. Определить сумму начисленных процентов.
Сумма начисленных процентов I равна разности между величиной наращенной суммы S и начальной суммой Р. Используя формулу для определения наращенной суммы S = Р*(1 i )^n, получим: I = S – P= Р*(1 i)^n – Р=P*((1 i)^n –1)=150000*((1 12%)^5-1) Результат: 114 351,25р.
Подбор параметра для банковских депозитов
На протяжении 10-ти лет мы хотим накопить 20 000$. Свои сбережения будем откладывать на банковский депозит по 5% годовых. Деньги будем вносить на банковский депозитный счет ежегодно и одинаковыми частями взносов. Какой должен быть размер ежегодного взноса, чтобы за 10 лет собрать 20 000$ при 5-т и процентах годовых?
Для решения данной задачи в Excel воспользуемся инструментом «Подбор параметра»:
- Составьте таблицу как показано на рисунке:
- В ячейку B5 введите функцию: =БС(B1;B2;B3;)
- Оставаясь на ячейке B5, выберите инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра»
- В появившемся окне заполните поля, так как на рисунке и нажмите ОК.

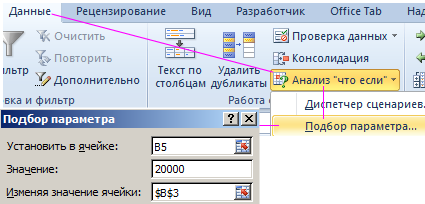
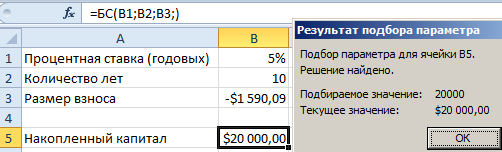
Результат вычисления получился с отрицательным числом – это правильно в соответствии со стандартом финансовых функций Excel. Регулярные взносы должны отображаться отрицательным значением, так как это категория расходных операций. А по истечению 10 лет мы получим на приход 20 000$.
Полезный совет! Если Вы нужно узнать размер ежемесячных взносов, тогда перед использованием инструмента «Подбор параметра» нужно процентную ставку разделить на 12 (чтобы перевести в ежемесячный процент).
А количество лет нужно перевести в количество месяцев умножив на 12. Таким образом, в ячейке B3 мы получим необходимую сумму ежемесячного взноса для достижения цели.
Подбор параметра для банковских кредитов
Допустим, Вы хотите приобрести автомобиль в кредит. Максимальная сумма ежемесячного взноса, которую Вы можете себе позволить, составляет 700$. Банк не может выдать Вам кредит сроком более чем на 3 года, с процентной ставкой 5,5% годовых. Можете ли вы себе позволить при таких условиях кредитования приобрести автомобиль стоимостью в 30 000$, а если нет, то на какую сумму можно рассчитывать?
Составьте таблицу условий кредитования в Excel как показано ниже на рисунке. Обратите внимание! Ячейка B4 содержит формулу: =-ПЛТ(B3/12;B2;B1).
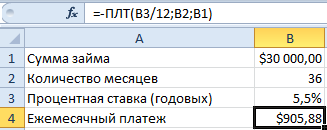
Как видно Вы не можете себе позволить такой дорогой автомобиль. Теперь узнаем, какая максимальная стоимость автомобиля соответствует Вашим финансовым возможностям. Для этого перейдите в ячейку B4 и выберите инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
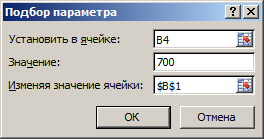
Заполните поля в появившемся диалоговом окне как показано выше на рисунке и нажмите ОК.
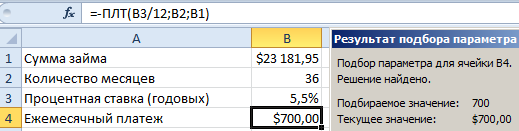
Как видно максимальная стоимость автомобиля, на которую можно рассчитывать составляет при таких финансовых возможностях и условиях кредитования составляет – 23 1812$.
Внимание! Если срок кредитования определяется количеством месяцев, а не лет, то годовую процентную ставку нужно перевести в месячную. Поэтому в первом аргументе функции ПЛТ стоит значение B3/12 (5,5% годовых разделено на 12 месяцев).
Используя финансовые функции, следует помнить об их стандартах. Например, сумма займа всегда отображаются как отрицательное число. Поэтому перед функцией ПЛТ мы использовали знак минус.
Поиск решений подбором параметра при ценообразовании
Стратегия для построения производственного плана выпуска продукта:
- В текущем году продукт должен быть продан в количестве 10 000шт.
- Производственные расходы 1-ой штуки: 7,5 руб.
- Расходы на реализацию: 450 000 руб.
Какую установить розничную цену, чтобы рентабельность производства сохранялась на уровне 20%?
Рентабельность определяется как соотношение дохода к прибыли (прибыль разделить на доход) и выражается только в процентах!
Снова решим поставленную задачу в Excel с помощью подбора параметра:
- Составьте таблицу с исходными данными и формулами, так как указано на рисунке ниже. Обратите внимание! В столбце D указаны, какие именно нужно вводить формулы в соответствующие ячейки столбца B. А в ячейке B1 указана цена 1 руб. чтобы избежать ошибок в формуле B3 и B10 (вероятная ошибка деления на 0). Не забудьте отформатировать все ячейки соответствующим форматам: денежный, общий, процентный.
- Перейдите в ячейку B10 и выберите инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра»
- Заполните поля в появившемся диалоговом окне как на рисунке и нажмите ОК.
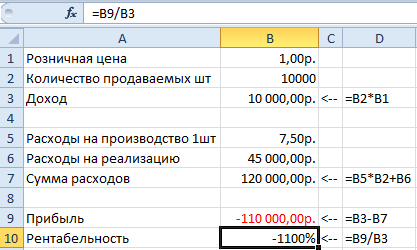
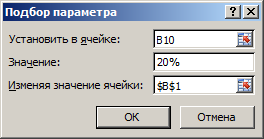
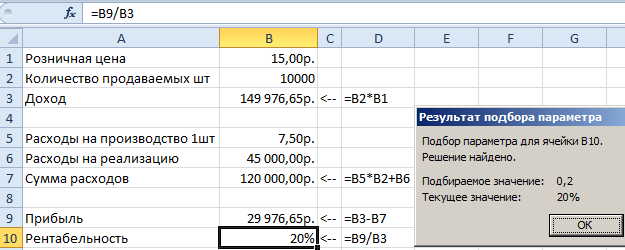
Как видно розничную цену (B1) нужно устанавливать в 2 раза выше производственных расходов на 1-ну штуку продукции. Только тогда мы сможем удержать рентабельность производства на уровне 20% при таких расходах на реализацию. В реальности бывает и еще хуже.
Расчет процентов по вкладу: калькулятор
Можно использовать и самый простой метод расчета процентов по вкладу — депозитный калькулятор, размещенный на сайте банка или каком-то стороннем финансовом сайте. Однако, здесь есть свои нюансы: вы никак не можете знать, какая формула расчета заложена в этот калькулятор, что и как он считает: так, как на самом деле должен производиться расчет процентов по вкладу (то, что я вам сегодня рассказал и показал) или так, как это выгодно банку.
Поэтому я настоятельно рекомендую производить расчет процентов по депозиту самостоятельно, при помощи вышеизложенных формул и методов, а затем делать проверку, внося данные в депозитный калькулятор банка. Если рассчитанные суммы совпадут — значит, банк считает проценты по вкладу честно, если там они получатся меньше — значит, расчет процентов по вкладу производится по какой-то другой методике, указанной в договоре, которая вам не выгодна. В последнее время подобные случаи можно наблюдать довольно часто: банки рекламируют одну процентную ставку, а по факту получается на 1-2% годовых меньше.
Теперь вы знаете, как рассчитать проценты по вкладу в каждом случае, сможете сделать это самостоятельно, сравнить условия банковских вкладов и проверить, правильно ли банк начисляет вам проценты.
Если у вас есть какие-то вопросы — задавайте их в комментариях. До новых встреч на Финансовом гении — сайте, который повысит вашу финансовую грамотность и научит эффективно распоряжаться личными финансами и семейным бюджетом.
Расчет сложных процентов по вкладу
Если вам необходимо рассчитать сложные проценты по вкладу — это будет несколько сложнее. Для этого используется следующая формула.
Формула сложных процентов по вкладу:
Sп = Sв*(1 %)n-Sв
где:
- Sп — сумма процентов по вкладу;
- Sв — сумма вклада;
- % — процентная ставка в период капитализации в виде десятичной дроби. % = p*Nд/Nг (p — процентная ставка по вкладу в виде десятичной дроби, Nд — период капитализации в днях (месяцах), Nг — количество дней (месяцев) в году);
- n — число периодов капитализации.
Как вы видите, для расчета нам понадобится функция возведения в степень. Она есть на стандартном калькуляторе для Windows. Чтобы ее увидеть — измените через меню вид калькулятора на «инженерный». Xy — это и есть функция возведения в степень.
Рассмотрим, как рассчитать сложный процент по вкладу по формуле сложных процентов на примере.
Пример. Вопрос: Я оформляю вклад в сумме 50000 рублей на год под 15% годовых с ежемесячной капитализацией процентов. Сколько процентов я получу за все время?
Ответ: Сначала рассчитаем процентную ставку в период капитализации, то есть, в один месяц: % = 0,15*1/12 = 0,0125. Теперь произведем расчет процентов по вкладу с капитализацией: 50000*(1 0,0125)12 — 50000 = 8037,73 рубля.