Mlitg | акции integral sa –
| Название | Послед. | Макс. | Мин. | Изм. | Изм.% | Объём | Время | ||
|---|---|---|---|---|---|---|---|---|---|
| Норникель | 22.030,0 | 22.450,0 | 21.866,0 | -142,0 | -0,64% | 711,42K | 05/03 | ||
| ЛУКОЙЛ | 6.197,5 | 6.214,0 | 5.852,0 | 391,5 | 6,74% | 3,57M | 05/03 | ||
| Сбербанк | 275,44 | 278,98 | 272,76 | 0,69 | 0,25% | 77,91M | 05/03 | ||
| Фонд первичных | 2.763,20 | 2.895,00 | 2.700,00 | -109,50 | -3,81% | 330,09K | 05/03 | ||
| Газпром | 225,34 | 228,42 | 220,02 | 4,20 | 1,90% | 51,54M | 05/03 | ||
| Роснефть | 556,50 | 558,30 | 541,55 | 16,40 | 3,04% | 12,61M | 05/03 | ||
| АК АЛРОСА | 107,62 | 107,62 | 104,17 | 4,00 | 3,86% | 25,51M | 05/03 | ||
| Татнефть | 562,50 | 567,80 | 536,30 | 28,80 | 5,40% | 11,29M | 05/03 | ||
| Магнит | 5.021,0 | 5.059,5 | 4.906,5 | 55,5 | 1,12% | 543,84K | 05/03 | ||
| Полюс | 14.414,5 | 14.625,0 | 14.115,0 | 350,5 | 2,49% | 156,84K | 05/03 |
Дисклеймер: Fusion Media не несет никакой ответственности за утрату ваших денег в результате того, что вы положились на информацию, содержащуюся на этом сайте, включая данные, котировки, графики и сигналы форекс. Операции на международном валютном рынке Форекс содержат в себе высокий уровень риска. Торговля на рынке Форекс может не подходить для всех инвесторов. Спекулируйте только теми деньгами, которые Вы можете позволить себе потерять.
Fusion Media напоминает вам, что данные, предоставленные на данном сайте, не обязательно даны в режиме реального времени и могут не являться точными. Все цены на акции, индексы, фьючерсы носят ориентировочный характер и на них нельзя полагаться при торговле. Версия этого документа на английском языке является определяющей и имеет преимущественную силу в том случае, если возникают разночтения между версиями на английском и русском языках. Таким образом, Fusion Media не несет никакой ответственности за любые убытки, которые вы можете понести в результате использования этих данных. Вы ищете акции, котировки или графики форекс? Взгляните на портал Investing.com – лучший технический анализ и современный экономический календарь к вашим услугам!
Английская версия данного соглашения является основной версией в случае, если информация на русском и английском языке не совпадают.
Teqra – краткий обзор, мысли вслух
Рынок инвестиций заняли несколько гигантов с осени 2020 года, однако в СНГ пространстве никто о них не знает. Предварительно можно связать их все одной группой создателей, хотя это лишь плод наших фантазий без каких-либо фактов. Даже если работаю разные люди, результат демонстрируют отличный.
Похожие шаги предпринимались в ряде других зарубежных направлений. С момента старта работы данного фонда информация в сфере хайп блогов и мониторингов не появилась. Рекламу там не берут, такая аудитория им не нужна, ведь деньги тратят на качественный трафик.
Именно поэтому отзывы о Teqra найти в рунете практически невозможно. Администрация заботится о репутации. Данные шаги подобны ранее упомянутым гигантам, поэтому решились рискнуть и заработать пока на рынке штиль и платят большие деньги без проблем. Однако гарантий здесь нет.
Деятельность и подготовка
Компания Teqra принимает средства в доверительное управление от частных инвесторов. Средства распределяются по нескольким направлениям трейдинга. В частности, деньги распределяются на торговлю акциями и криптовалютой. Также часть идет на добычу крипто монет и традиционный майнинг.
Долгая память микросхем: как «интеграл» превращает инновации в прибыль | экономическая газета
 Холдинг «ИНТЕГРАЛ» ожидает, что завершившиеся в прошлом году исследования и разработки начнут приносить положительный экономический эффект. Развивая перспективные проекты, компания рассчитывает в т.ч. на господдержку. Об этом в интервью «ЭГ» рассказал генеральный директор управляющей компании холдинга «ИНТЕГРАЛ» Виталий СОЛОДУХА.
Холдинг «ИНТЕГРАЛ» ожидает, что завершившиеся в прошлом году исследования и разработки начнут приносить положительный экономический эффект. Развивая перспективные проекты, компания рассчитывает в т.ч. на господдержку. Об этом в интервью «ЭГ» рассказал генеральный директор управляющей компании холдинга «ИНТЕГРАЛ» Виталий СОЛОДУХА.
– Виталий Александрович, какие достижения в области инновационной деятельности за 2021 г. для «Интеграла» наиболее значимы?
– Основным направлением создания инноваций у нас являются разработка и освоение в серийном производстве изделий микроэлектроники. Динамика научно-технической деятельности в холдинге носит цикличный характер. В 2021 г. закрылся предыдущий пятилетний цикл (2021–2021 гг.) с завершением большинства НИОКР и запуска в серийное производство новых изделий в 2021–2021 гг.
В прошлом году начались новые проекты. В УК «ИНТЕГРАЛ» выполнялось 56 НИОКР, в рамках которых разрабатывалось 74 изделия.
Значимость созданных инноваций мы оцениваем в первую очередь по коммерческой успешности разработанных изделий, результатам продаж. Чтобы их корректно оценивать, требуется некоторый временной лаг. Как правило, разработанные изделия окупаются в течение 3–5 лет.
Мы выделяем 2 типа реализуемых проектов: краткосрочные и долгосрочные. Так, по некоторым изделиям достигается приличный объем продаж уже на следующий год после освоения. Но, к сожалению, всплеск спроса на них быстро проходит. Это в первую очередь касается электронных компонентов для бытовой электроники. Другие изделия продвигаются на рынок довольно долго, спрос на них сравнительно невелик, но они стабильно продаются в течение 10 и более лет. Это характерно для изделий военной, промышленной, автомобильной электроники. Зачастую благодаря временной составляющей второй тип проектов оказывается более выгодным.
Положительного экономического эффекта мы ожидаем от всех завершившихся в 2021 г. НИОКР. Но наиболее перспективные – это интегральные микросхемы однократно электрически программируемого запоминающего устройства информационной емкостью 64 Кґ 8, устойчивого к специальным факторам, с номинальным напряжением питания 3,3 В и базовый кристалл для серии регулируемых стабилитронов универсального применения.
– Что «ИНТЕГРАЛ» ждет от Госпрограммы инновационного развития Республики Беларусь на 2021–2020 гг.?
– В рамках этой программы государство пытается найти в нашей экономике потенциальные точки роста и придать им дополнительный импульс. Это соответствует нормальной мировой практике. Грамотный собственник (в нашем случае – государство) всегда заботится о развитии и повышении эффективности своих активов. Время экстенсивного пути давно прошло. Сегодня рост может быть достигнут только благодаря созданию принципиально новых производств, разработке новых изделий и технологий, т.е. инноваций. Холдинг развивает ряд проектов, имеющих неплохие перспективы. Но, чтобы реализовать их потенциал, предстоит выполнить огромные объемы работ и задействовать существенные ресурсы, в т.ч. финансовые. Поэтому государственная поддержка здесь окажется совсем не лишней.
– Требуется ли господдержка дляразработки новых технологий?
– В сфере микроэлектроники только глобальные компании работают с видимой прибылью (TSMC, Intel, Samsung и немногие другие). После появления каждой новой технологии первые заводы-монополисты, обладающие ей, и получают основную прибыль, а те, кто приходит на 2–5–10 лет позже, вынуждены работать практически по себестоимости.
Рис. 1. Стоимость полупроводникового завода в зависимости от проектных норм (млн. USD).

Тем не менее «ИНТЕГРАЛ» работает стабильно и рентабельно. Наше экономическое положение устойчиво. Однако разработка принципиально новых технологий связана с закупкой дорогостоящего оборудования. Для столь масштабных капиталовложений собственных средств зачастую недостаточно.
– Какие направления на международном рынке микроэлектронных компонентов и промышленной электроники сейчас находятся на пике спроса? Чем может ответить на него «ИНТЕГРАЛ»?
– Здесь нужно рассматривать конечные (завершенные) устройства, в которых используются микроэлектронные компоненты. Именно они формируют этот спрос. Наибольший вклад в него в стоимостном выражении вносят смартфоны, затем идут компьютеры, цифровые телевизоры, автомобильная электроника и планшеты.
Соответственно, самые большие продажи наблюдаются в секторах интегральных схем памяти (ОЗУ и FLASH), микропроцессоров и специализированных логических ИС.
В сумме эти сектора обеспечивают более 60% продаж на рынке полупроводников. Данные изделия отличаются высоким уровнем конструктивной сложности, высокой ценой и изготавливаются по технологиям, недоступным сегодня холдингу «ИНТЕГРАЛ», в первую очередь из-за высокой капиталоемкости. Ключевая особенность микроэлектронного (полупроводникового) производства – структура затрат. Здесь особенно велика доля амортизации, расходов на содержание оборудования, технологии, НИОКР. Стоимость последних существенно возрастает вместе с проектными нормами. Это связано не только с трудоемкостью и зарплатой, но и с внешними факторами – стоимостью САПР, библиотек проектирования (IP-блоков), фотошаблонов и др.
Рис. 2. Стоимость разработки изделия зависимости от проектных норм (млн. USD).

Помимо микросхем памяти, микропроцессоров, специализированных логических ИС в электронных устройствах необходимы и другие элементы. В материнской плате есть сотни полупроводниковых приборов – MOSFET, драйверы, микросхемы питания и т.п. Почти для всех из них хватает и 1 мкм (1000 нм) технологии.
Иногда применение самых передовых проектных норм технологически или экономически нецелесообразно. Наиболее наглядно это видно в силовой электронике, где уменьшение размеров элемента противоречит требованиями по пробивным напряжениям и протекающим токам, и военной электронике, где начиная с определенного значения проектных норм снижается устойчивость (надежность) изделия к специальным внешним воздействующим факторам.
Сегодня в мире большинство микросхем делается по «грубым» технологиям (0,35–0,5 мкм и более), и миллиарды микросхем, уходящих в Китай, в т.ч. и от «ИНТЕГРАЛА» (правда, в основном в виде пластин), – вполне востребованы и продаются. Так что в холодильниках, телевизорах, пылесосах, материнских платах и сотовых телефонах есть наши микросхемы и силовые транзисторы – но под зарубежными именами.
– Известно, что «ИНТЕГРАЛ» экспортирует 80% своей продукции. Какие направления экспорта более успешны? Почему?
– Можно выделить два основных направления экспорта. В Российскую Федерацию мы поставляем преимущественно электронные компоненты двойного и специального назначения. У нас сложились устоявшиеся партнерские отношения с российскими предприятиями оборонно-промышленного комплекса, а также входящими в федеральное космическое агентство «Роскосмос» и государственную корпорацию «Росатом». Благодаря высокому качеству наша продукция пользуется там устойчивым спросом.
В страны Юго-Восточной Азии мы поставляем электронные компоненты гражданского применения, преимущественно силовой электроники. Например, в комплекте к каждому смартфону идет зарядное устройство на основе микросхемы импульсного регулятора напряжения. В каждом ЖК-мониторе компьютера есть микросхема управления подсветкой.
– Какую долю в вашей выручке приносит продажа технологий?
– Мы – производственное предприятие. Все разработанные технологии внедряем у себя. Продажа технологии означает, что она перестает быть уникальной – появляется конкурент, который ее использует. Получается, что, заработав какие-то деньги сейчас, теряешь больше в перспективе. Это подтверждено на опыте работы с нашими китайскими «партнерами». Поэтому технологии мы продаем только в составе изделий.
– Доступен ли для «ИНТЕГРАЛА» российский рынок госзакупок? Сколько тендеров удалось выиграть в 2021 году? Насколько это выгодно?
– Основные потребители нашей продукции – предприятия оборонно-промышленного комплекса РФ и производители бытовой и промышленной электроники. Поставки идут напрямую потребителям, а также с помощью института квалифицированных поставщиков, сертифицированных соответствующими органами РФ.
– Каковы финансовые результаты вашего предприятия за прошлый год? Удалось ли улучшить эти показатели?
– За 2021 г. по холдингу «ИНТЕГРАЛ» объем выручки от реализации увеличился в сравнении с 2021 г. на 18,4%, до 184,7 млн. BYN, в т.ч. по управляющей компании – на 17,1%, до 174,2 млн. BYN. Соотношение между отгруженной и произведенной продукцией составило в холдинге 105,3% против 91,4% в 2021-м.
Темп роста выручки на одного работающего по холдингу составил 121,8%, коэффициент опережающего роста выручки от реализации продукции, товаров, работ и услуг на одного среднесписочного работника над ростом номинальной начисленной среднемесячной зарплаты составил 1,09, а в УК – 1,08 при плане больше 1,0.
При этом средняя зарплата выросла на 11,8% и составила 701,5 BYN, в т.ч. в управляющей компании – 728 BYN. Рентабельность продаж за 2021–2021 годы составила более 10%, чистая прибыль за данный период – 11,6 млн. BYN, а в УК «ИНТЕГРАЛ» – 13,4% и почти 3,5 млн. BYN соответственно. Удельный вес отгруженной инновационной продукции в общем объеме – 35,1%.
На текущий год в холдинге запланирован объем производства промышленной продукции на уровне 206,5 млн. BYN, чистая прибыль – 2,575 млн. BYN, рентабельность продаж – не менее 8%. При этом соотношение запасов готовой продукции и среднемесячного объема производства должно составить 250%. Мы намерены снизить затраты на 5,1% и увеличить экспорт на 11,7%, до 87,7 млн. USD.
– Какие преимущества дало «ИНТЕГРАЛУ» создание холдинга?
– В целях сохранения технологических и производственных связей между бывшими предприятиями НПО «ИНТЕГРАЛ», для содействия их кооперации, обеспечения единой инвестиционной и научно-технической политики и, как следствие, увеличения экспортного потенциала, сохранения достигнутой управляемости было принято решение о создании холдинга, что должно обеспечить достижение целого ряда стратегически важных производственно-экономических показателей и эффектов. В частности, это увеличение доли рынка и расширение сферы сбыта продукции, конкурентоспособность продукции по цене через экономию на эффекте масштаба и снижении доли управленческих расходов. Важное направление – диверсификация производства через освоение и выпуск новых конкурентоспособных продуктов. Кроме того, мы надеемся увеличить инвестиционную привлекательность холдинга и его участников, а также их рыночную стоимость.
Автор публикации: Оксана КУЗНЕЦОВА
Инвестиционные условия
Желающие зарабатывать на пассиве получают в распоряжение множество инвестиционных тарифов. Скажем сразу, не все стоит рассматривать к работе, ведь маркетинг с подвохом. Если делать все правильно никакого подвоха не будет. Инвесторы Teqra могут начать с 50$ и получать плавающий ежедневный процент от 1,1% до 1,5% в течение 10 рабочих дней. По окончанию срока инвестирования депозит возвращается на баланс и становится доступным к выводу.
Прибыль начисляется везде ежедневно. Стоит рассматривать максимум тарифы до Plan 3, если ваш кошелек велик и может себе позволить выделить 10%, которые составят не менее 5000$. Подобные проекты такие суммы переваривают, однако первых двух тарифов достаточно для работы.
Рекомендуется инвестировать деньги на линейку тарифов до Plan 3. Также стоит определиться с суммой инвестирования сразу, ведь проект платит, а докладывая средства в будущем вы увеличите для себя риски.
Инструкция по работе
Переходим на официальный сайт Teqra com.
Официальный сайт
Жмем на главной странице «Регистрация».
Заполняем поля, проверяем достоверность информации и аплайна, после чего жмем «регистрация». В личном кабинете пополняем баланс на вкладке «Пополнение».
Указываем способ пополнения и сумму. Затем следуя инструкции оплачиваем заявку. После того, как деньги оказались на балансе создаем депозит.
Во вкладке «Открыть депозит» выберите тариф, введите сумму и нажмите «инвестировать».
Маркетинг платформы
Инвестиционная программа Teqra использует традиционный маркетинг. Подключена пассивная составляющая с инвестицией и стабильным процентом прибыли, а также активная – партнерская программа. Лидеры индустрии не смогут вымывать кассу проекта своими заработками на партнерке, ведь математически она довольно сдержанная. Условия направлены на мотивацию инвестора делать реинвест, чем обуславливать дальнейшую работу и заработок.
Партнерская программа
С первого взгляда партнерская программа Teqra глубокая, чрезмерно щедрая и может навредить проекту. Углубляясь, приходит понимание, что админ проделал отличную работу и подобрал идеальные условия. Партнерка состоит из карьерных статусов, где при достижении определенного оборота открываются новые уровни и растут проценты отчисления.
За каждый сделанный депозит партнерами система возвращает в виде бонуса на баланс часть от суммы. Требования к статусам слишком необъятные, поэтому рабочими остаются проценты на статусе Manager, доступного всем. Каждый вклад с 5 уровней рефералов в глубину приносит 5-2-1-1-1% соответственно. Условия не позволяют лидерам зарабатывать слишком много, а значит пассивная составляющая у руководства в приоритете.
Применение интеграла в экономике
4.1) Найти излишек потребителя, если кривая спроса задана уравнением P=40-4Q2, а равновесное количество товара Q0 равно 2.
4.2) Определить добавочную выгоду производителя PS, если кривая предложения имеет вид P=10 8Q3, а точка равновесия между спросом и предложением достигается при количестве товара Q0=5.
4.3) Заданы чистые инвестиции I(t)=10000 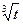 . Определить приращение капитала за 5 лет.
. Определить приращение капитала за 5 лет.
4.4) Функция, задающая инвестиции остается прежней (см. условие задачи 3). Через сколько лет приращение составит 80000?
4.5) Вычислить начальный вклад P, если выплаты должны составлять 200 ед. в течение 5 лет, а процентная ставка равна 3.
4.6) Предельные издержки описываются формулой 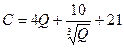 . Записать формулу издержек, зная, что постоянные издержки равны 80.
. Записать формулу издержек, зная, что постоянные издержки равны 80.
4.7) Записать вид экономической функции, если её предельный величина описывается формулой 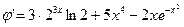 .
.
4.8) Найти излишек потребителя, если кривая спроса задана уравнением P=1000-10Q4, а равновесное количество товара Q0=3.
4.9) Определить добавочную выгоду производителя, если кривая предложения имеет вид P=40Q3 80, а точка равновесия между спросом и предложением достигается при количестве товара Q0=100.
4.10) Чистые инвестиции заданы формулой 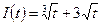 . Определить приращение капитала за 4 года.
. Определить приращение капитала за 4 года.
4.11) 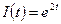 – функция, задающая инвестиции. Через сколько лет приращение составит 2000?
– функция, задающая инвестиции. Через сколько лет приращение составит 2000?
4.12) Вычислить начальный вклад P, если выплаты должны составлять 300 ед. в течение 2 лет, а процентная ставка равна 5.
Дополнительные задания для самостоятельного решения
1.Найти неопределенный интеграл.
1. а) 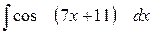 ; б)
; б) 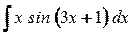 .
.
2. а) 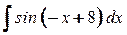 ; б)
; б) 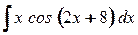 .
.
3. а) 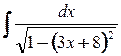 ; б)
; б) 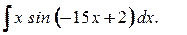
4. а) 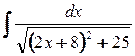 ; б)
; б) 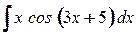 .
.
5. а) 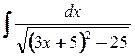 ; б)
; б) 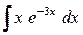 .
.
6. а) 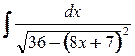 ; б)
; б)  .
.
7. а) 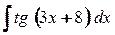 ; б)
; б) 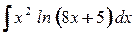 .
.
8. а) 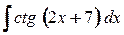 ; б)
; б)  .
.
9. а) 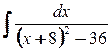 ; б)
; б) 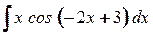 .
.
10. а) 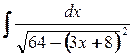 ; б)
; б) 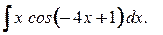
2.Найти площадь фигуры, образованной линиями:
1. 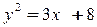 ,
, 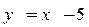 .
.
2. 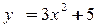 ,
, 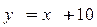 .
.
3. 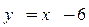 ,
, 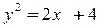 .
.
4. 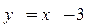 ,
, 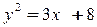 .
.
5. 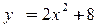 ,
, 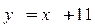 .
.
6.  ,
, 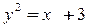 .
.
7.  ,
, 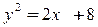 .
.
8. 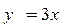 ,
, 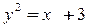 .
.
9. 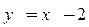 ,
, 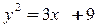 .
.
10. 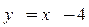 ,
, 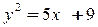 .
.
Матрицы и определители.
Определение матрицы
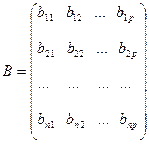
1. Матрицей называется прямоугольная таблица элементов. Обозначаются матрицы заглавными латинскими буквами.
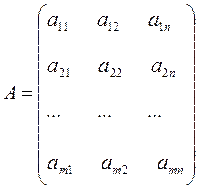
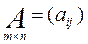 ,
, 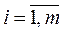
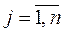
m x n – размер матрицы.
m = n – матрица – квадратная.
Квадратная матрица, имеющая единицы по главной диагонали и остальные элементы, равные нулю, называется единичной и обозначается буквой E или I.
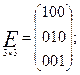
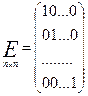
Матрица может иметь только одну строку (матрица-строка) или только один столбец (матрица-столбец).
Вектор – столбец m x 1 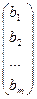
Вектор – строка 1 x n 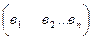
Операция, при которой меняются местами строки и столбцы A с сохранением порядка элементов называется транспонированием.
 ;
; 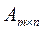
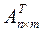
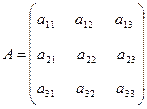 ;
; 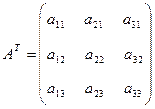
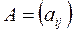
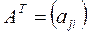
Для симметричных матриц 
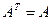
Две матрицы, имеющие одинаковые размеры называются равными тогда и только тогда, когда равны их соответственные элементы.
Действия над матрицами.
1) 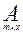
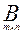 =
= 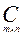

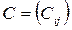 ;
; 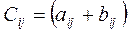
2) kA=C; 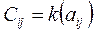
Сложение и умножение на число являются линейными операциями. Они не меняют размеров матрицы.
3) Введём операцию умножения:
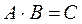
Правило “строка на столбец”.
Умножение двух матриц A и B возможно только тогда, когда число столбцов матрицыA равно числу строк матрицыB.

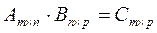



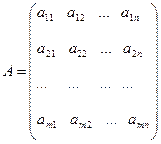
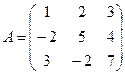
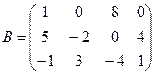
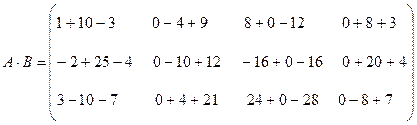 =
= 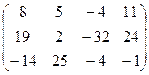 ;
;

Обратная матрица.
Пусть A – квадратная матрица. Единственная матрица 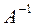 от умножения которой на матрицу A как слева, так и справа получается единичная матрица E, называется матрицей, обратной для матрицы A.
от умножения которой на матрицу A как слева, так и справа получается единичная матрица E, называется матрицей, обратной для матрицы A.
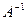 ·A=A·
·A=A· 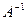 =E
=E
§
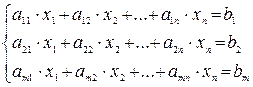
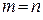
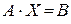 , где
, где 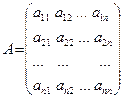 ,
, 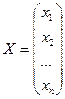 ,
, 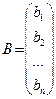
Система линейных алгебраических уравнений (СЛАУ) совместна, если имеет хотя бы одно решение и несовместна, если не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более чем одно решение.
Система называется однородной, если все элементы столбца свободных членов b1, b2 … bn равны нулю и неоднородной, если хотя бы один этих элементов отличен от нуля.
Для решения СЛАУ с квадратной матрицей коэффициентов разработан ряд методов. Рассмотрим метод определителей (формула Крамера), матричный метод и метод Гаусса:
4.1.1. Метод определителей (формула Крамера)
Пусть система
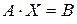
имеет квадратную матрицу коэффициентов, определитель которой не равен нулю. Тогда система имеет единственное решение, которое по формулам Крамера записывается:
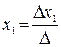 ,
, 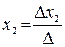 , … ,
, … , 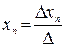 ,
,
где 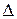 – определитель матрицы коэффициентов системы А, а
– определитель матрицы коэффициентов системы А, а  ,
, 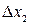 , … ,
, … ,  – определители замещения, которые получаются, когда в матрице А столбец, содержащий соответствующую переменную, заменяется столбцом свободных членов.
– определители замещения, которые получаются, когда в матрице А столбец, содержащий соответствующую переменную, заменяется столбцом свободных членов.
Пример.
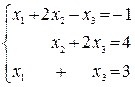
Решение.
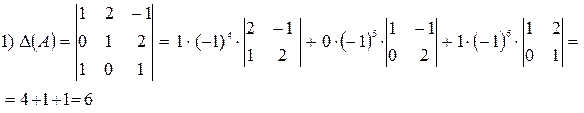


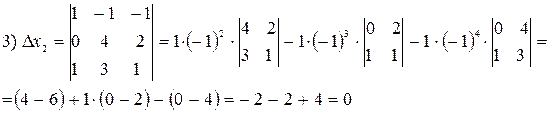
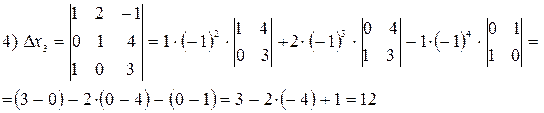
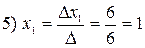 ,
, 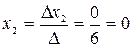 ,
, 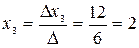
Проверка
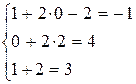
Метод определителей позволяет решать системы только с квадратной матрицей коэффициентов при условии, что 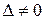 .
.
4.1.2. Матричный метод (математический метод, метод обратнойматрицы)
Пусть система
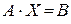
Имеет квадратную матрицу коэффициентов, определитель которой не равен нулю. Тогда система имеет единственное решение, которое представляется в следующем виде:
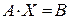
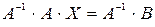
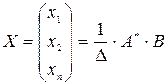
Матричный метод позволяет решать системы только с квадратной матрицей коэффициентов при условии, что 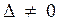 .
.
Пример.
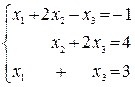
Решение.
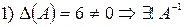
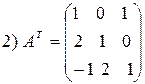
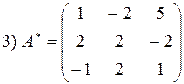
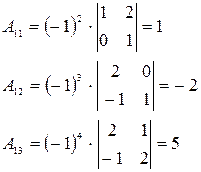
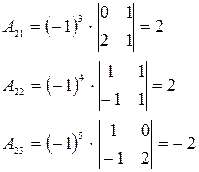
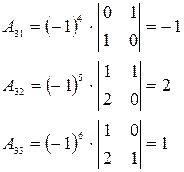
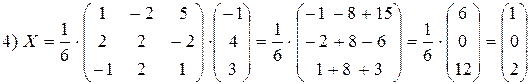
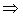
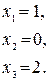
4.1.3. Метод Гаусса (универсальный метод)
Метод Гаусса позволяет решать системы не только с квадратной, но и с прямоугольной матрицей коэффициентов, а также позволяет решать системы, когда определитель матрицы 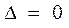 . Метод Гаусса основан на следующих эквивалентных преобразованиях системы уравнений:
. Метод Гаусса основан на следующих эквивалентных преобразованиях системы уравнений:
Ø Перестановка уравнений в системе;
Ø Умножение любого уравнения на любое число, отличное от нуля;
Ø Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число;
Ø Отбрасывание уравнений, в которых все коэффициенты и свободный член равны нулю.
Цель преобразований:
Свести матрицу к ступенчатому виду и последовательно, методом обратного хода, начиная с последней строки записать решение системы.
Метод Жордана – Гаусса:
Свести исходную систему уравнений к равносильной системе с единичной матрицей коэффициентов.
Пример 1.
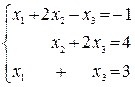
Решение (метод Гаусса):



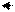





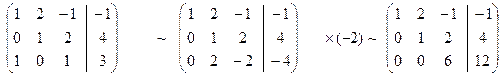
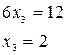
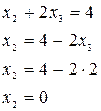
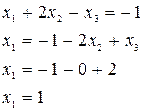
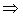
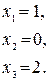
Метод Жордана – Гаусса:









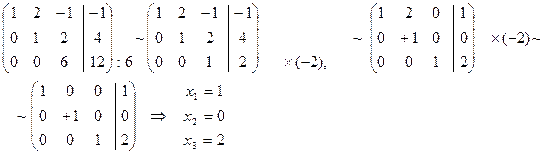
Пример 2.

Решение (Метод Гаусса):





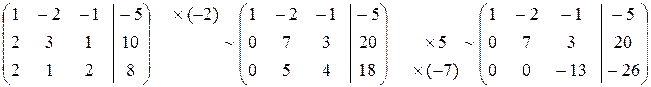
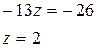
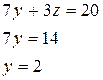
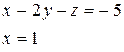
Метод Жордана – Гаусса:




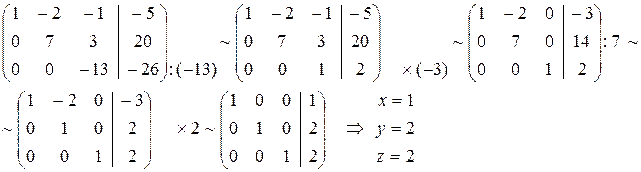
§
Система m линейных уравнений с n переменными называется системой линейных однородныхуравнений, если все их свободные члены равны нулю.
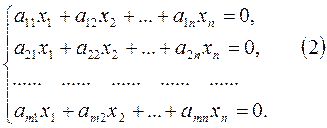
Система линейных однородных уравнений всегда совместна, т.к. она всегда имеет, по крайней мере, нулевое (тривиальное) решение (0;0;…;0).
Если в системе (2) m=n, а её определитель отличен от нуля, то такая система имеет только нулевое решение, как это следует из теоремы и формул Крамера.
Ненулевые решения, возможны лишь для таких систем линейных однородных уравнений, в которых число уравнений меньше числа переменных или, когда m=n, но определитель системы равен нулю.
Иначе: система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг её матрицы коэффициентов при переменных меньше числа переменных, т.е. 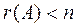 .
.
Обозначим решение системы
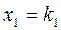 ,
, 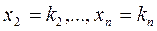
в виде строки 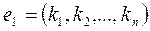 .
.
Свойства решений системы линейных однородных уравнений.
1. Если строка 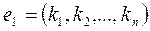 -решение системы, то и строка
-решение системы, то и строка 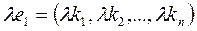 -также решение этой системы.
-также решение этой системы.
2. Если строки 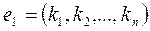 и
и 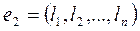 -решения системы (2), то при
-решения системы (2), то при 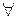
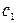 и
и 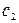 их линейная комбинация
их линейная комбинация 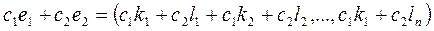 -так же решение этой системы.
-так же решение этой системы.
Из свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы.
Определение. Система линейно независимых решений  называется фундаментальной, если каждое решение системы является линейной комбинацией решений
называется фундаментальной, если каждое решение системы является линейной комбинацией решений 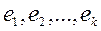 .
.
Теорема: Если ранг матрицы коэффициентов при переменных системы линейных однородных уравнений (2) меньше числа переменных n, то всякая фундаментальная система решений системы (2) состоит из n-r решений.
Поэтому общее решение системы (2) линейных однородных уравнений имеет вид:
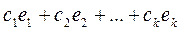 ,
,
где 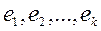 – любая фундаментальная система решений,
– любая фундаментальная система решений, 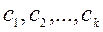 -произвольные числа,
-произвольные числа,  .
.
Пример решения задач.
Пример. Найти фундаментальную систему решений системы линейных однородных алгебраических уравнений.

Такая система совместна всегда, так как имеет тривиальное решение (0; 0; 0; 0; 0).
Решение.
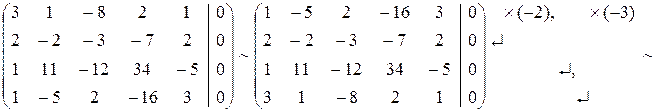
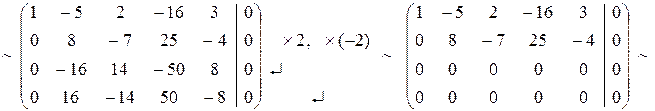
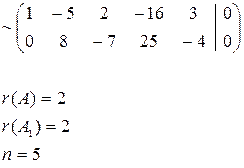
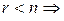 система имеет множество решений.
система имеет множество решений.
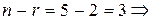 система имеет три свободные переменные
система имеет три свободные переменные
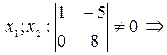
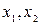 – базисные переменные,
– базисные переменные, 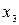 ,
, 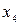 ,
, 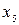 – свободные переменные
– свободные переменные
Условия для нахождения фундаментальных решений:
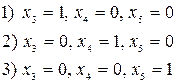
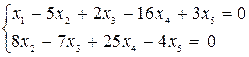

1)
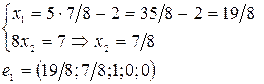
2)
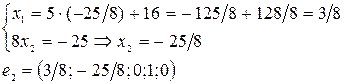
3)
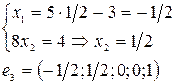
Данные строки – 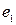 ,
, 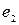 ,
, 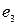 (векторы) – образуют фундаментальную систему решений данной системы линейных однородных алгебраических уравнений.
(векторы) – образуют фундаментальную систему решений данной системы линейных однородных алгебраических уравнений.
РАСЧЕТНО-ГРАФИЧЕСКИЕ РАБОТЫ
Расчетная работа № 1.
Обработка экспериментальных данных
Методом наименьших квадратов
Основные положения
При обработке данных экспериментов возникает необходимость определения закономерности их изменения:
– представление в виде какой-либо функциональной зависимости с целью исследования и прогнозирования характера и протекания процесса;
Из методов построения эмпирической прямой наиболее обоснован и распространён метод наименьших квадратов, заключающийся в следующем:
– из множества функциональных зависимостей определённого вида выбирается та, для которой сумма квадратов отклонений экспериментальных значений от теоретических (вычислительных) является наименьшей.
Впервые этот метод предложил Гаусс.
§
Пусть данные опыта представляют собой некоторое кол-во n-точек с координатами (xi;yi), (i= 1; 2; …; n)
Если в таблице участвуют две величины, то получают зависимость в видефункции одной переменной y(x) или x(y).
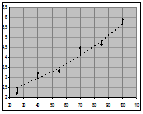
Удобно изображать эти процессы графически
Можно этот набор точек попытаться описать прямой типа (y=ax b), можно считать, что это часть параболы (y=ax2 bx c), степенно-показательной (y=beax) или обобщённо-степенной (y=bxa) функции.
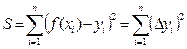
Согласно методу наименьших квадратов, параметры функции f(x) следует выбирать так, чтобы сумма квадратов отклонений была наименьшей, а значит минимизировались отклонения статистических данных от теоретических.
Этот метод постоянно используется в статистике, эконометрике, в финансовой математике и т.д.
Часто такой метод называют получением уравнений регрессии методом наименьших квадратов по сущности вычислительной процедуры. Это классическая задача дифференциального исчисления.
Рассмотрим применение данного метода для получения эмпирических формул на примере линейной функции y=ax b
Пусть принято решение искать эмпирическую формулу в виде линейной функции.
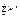 Очевидно, что в искомом уравнении линейной функции y=ax b неизвестными являются коэффициенты a и b, при этом их значение должно обеспечить минимальное суммарное отклонение экспериментальных данных от теоретических, т.е. обеспечить прохождение прямой наиболее близко ко всем экспериментальным точкам. Данная цель достигается при минимальной величине суммы квадратов отклонений.
Очевидно, что в искомом уравнении линейной функции y=ax b неизвестными являются коэффициенты a и b, при этом их значение должно обеспечить минимальное суммарное отклонение экспериментальных данных от теоретических, т.е. обеспечить прохождение прямой наиболее близко ко всем экспериментальным точкам. Данная цель достигается при минимальной величине суммы квадратов отклонений.
При этом a и b являются переменными.
Определим функцию 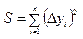
Для нахождения экстремума функции 2-х переменных необходимо найти частные производные данной функции по каждой переменной, приравнять их к нулю, и решив полученную систему двух уравнений, определить критические значения a и b.
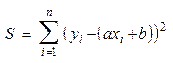
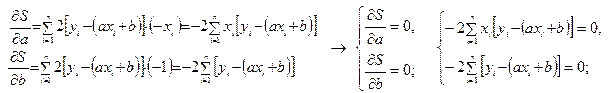
После преобразований получим следующую систему
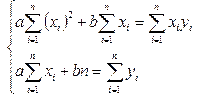
Найденные значения a и b соответствуют min функции S .
Расчет значений известных величин, входящих в уравнения системы, удобно вести с помощью таблиц.
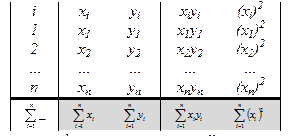
Подставляя найденные значения коэффициентов при a и b в систему уравнений, получаем значения неизвестных a и b. Таким образом эмпирическая формула будет найдена.
Графиком её является прямая, проходящая наиболее близко ко всем экспериментальным точкам.
Рассмотрим функцию вида у=bxa (обобщенно-степенная функция)
Прологарифмируем её.
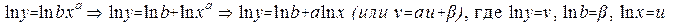
Теперь линейное уравнение рассмотрим не для табличных значений, а для их логарифмов:
Расчет значений, входящих в уравнения системы, удобно вести с помощью таблиц.
Рассмотрим функцию вида у=beax (степенно-показательная функция)
Прологарифмируем её:
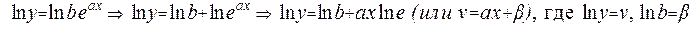
Теперь линейное уравнение рассмотрим не для табличных значений, а для их логарифмов:
Расчет значений, входящих в уравнения системы, удобно вести с помощью таблиц.
§
Протабулируем данные:

Найдем соответствующее отклонение от заданных точек:

Сравнив отклонения, можно сделать вывод, какая функция лучше подходит.
Расчетная работа № 2.
Матрицы. Определители.
Решение систем линейных алгебраических уравнений.
Часть 1
1. Выполнить сложения матриц разных размеров.
2. Выполнить умножение матриц:
1) Прямоугольных матриц
2) Квадратных матриц
3. Посчитать определитель всеми способами ( правило треугольника, правило Сарриуса, универсальный метод (через миноры)).
4. Найти обратную матрицу и выполнить проверку.
Часть 2
5. Решить систему линейных уравнений с квадратной матрицей коэффициентов:
1) Метод определителей (Формулы Крамера)
2) Матричный метод
3) Метод Гаусса
4) Метод Жордана-Гаусса.
Часть 3
6. Решить систему с прямоугольной матрицей коэффициентов:
1) Найти общее решение, задать его параметрически
2) Найти все базисные решения этой системы.
7. Найти общее решение и фундаментальную систему решений системы линейных однородных алгебраических уравнений.
Расчетная работа № 3 (дополнительная).
Приближенные вычисления определенных интегралов.
Разбивая отрезок интегрирования на 10 равных частей, а затем на 20 частей, найти приближенно интегралы 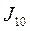 и
и .Определить точность с помощью разности
.Определить точность с помощью разности 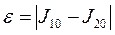 .
.
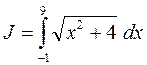
а) по формуле трапеций;
б) по формуле Симпсона.
Решение. Имеем подинтегральную функцию 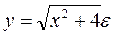 . Составим вспомогательную таблицу
. Составим вспомогательную таблицу
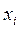 |  |  | При делении на 10 частей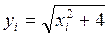 | При делении на 20 частей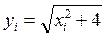 |
| -1 |  2,23607 2,23607 |  2,23607 2,23607 | ||
| -0,5 | 0,25 | 4,25 | 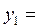 2,06155 2,06155 | |
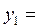 2,0 2,0 |  2,0 2,0 | |||
| 0,5 | 0,25 | 4,25 | 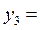 2,06155 2,06155 | |
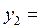 2,23607 2,23607 | 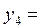 2,23607 2,23607 | |||
| 1,5 | 2,25 | 6,25 |  2,5 2,5 | |
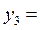 2,82843 2,82843 | 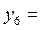 2,82843 2,82843 | |||
| 2,5 | 6,25 | 10,25 | 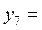 3,20216 3,20216 | |
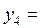 3,60555 3,60555 | 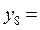 3,60555 3,60555 | |||
| 3,5 | 12,25 | 16,25 | 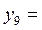 4,03113 4,03113 | |
 4,47214 4,47214 | 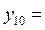 4,47214 4,47214 | |||
| 4,5 | 20,25 | 24,25 | 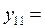 4,92443 4,92443 | |
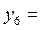 5,38516 5,38516 | 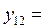 5,38516 5,38516 | |||
| 5,5 | 30,25 | 34,25 | 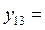 5,85235 5,85235 | |
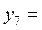 6,32456 6,32456 | 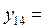 6,32456 6,32456 | |||
| 6,5 | 42,25 | 46,25 | 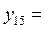 6,80074 6,80074 | |
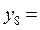 7,28011 7,28011 | 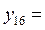 7,28011 7,28011 | |||
| 7,5 | 56,25 | 60,25 | 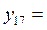 7,76209 7,76209 | |
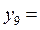 8,24621 8,24621 | 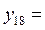 8,24621 8,24621 | |||
| 8,5 | 72,25 | 76,25 | 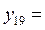 8,73212 8,73212 | |
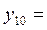 9,21954 9,21954 | 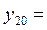 9,21954 9,21954 |
а) По формуле трапеций.
При делении на 10 частей:
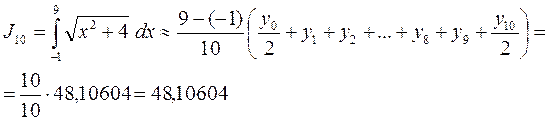
При делении на 20 частей

Точность вычислений оценивается с помощью разности: 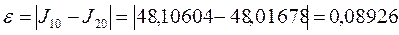
б) По формуле Симпсона.
При делении на 10 частей:

При делении на 20 частей
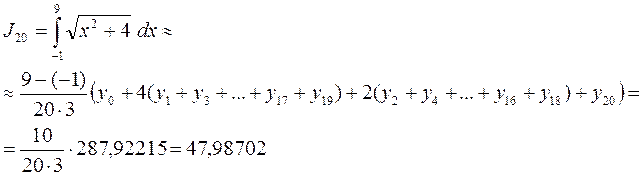
Точность вычислений оценивается с помощью разности: 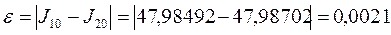
Известно, что при одинаковом числе точек разбиения формула Симпсона дает более точный результат.
ЛИТЕРАТУРА
1. Практикум по высшей математике для экономистов. Учеб. Пособие для вузов. /Кремер Н.Ш., Тришин И.М., Путко Б.А. и др.; Под ред. Н.Ш.Кремера. – М. ЮНИТИ-ДАНА, 2004. – 403 с.
2. Математика: учебное пособие для студентов вузов, обучающихся по экономическим специальностям /Под ред. Горлача Б.А. Учебное пособие: – М.: ЮНИТИ-ДАНА, 2006.-911 с. – Допущ.Мин-м образования и науки РФ.
3. Высшая математика для экономистов. Учебник для вузов /Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2002. – 471 с.
4. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике. Учебник: В 2-х ч. – М.: Финансы и статистика, Ч.I. 2005. – 384 с.; Ч. II. 2006 – 560 с.
5. Красс М.С., Чупрынов Б.П. Математика для экономистов. – СПб.: Питер, 2005. – 464 с.
Учебное издание
Лищинская Евгения Эльявна
Коваленко Татьяна Дмитриевна
Лищинский Наум Яковлевич
МАТЕМАТИКА
Часть 2
Учебно-методическое пособие
Корректор Петрова И.Н.
| Подписано в печать 10.02.2009 Бумага тип. № 1 Усл.печ.л. 2,75 Тираж 150 экз. | Формат 60х90 1/16 Отпечатано на ризографе Заказ 21 |
Международный институт рынка
443030, Самара, ул. Желябова, 21
Множительный участок МИР
443030, Самара, ул. Желябова, 21





