Основы финансовых вычислений. задачи – презентация, доклад, проект
Решение задачи 70
При ежегодных взносах наращенная сумма равна . При ежеквартальных взносах наращенная сумма равна
, что в 1,03676 раза, или на 3,676%, больше, чем при годовых взносах. При ежемесячном начислении процентов наращенная сумма равна что в
раза, или на 2,29%, больше, чем при годовой капитализации.
Как рассчитывается процентная ставка по вкладу (формула, пример с пояснением), влияние на доходность
Употребление термина «процент» в России начинается с XVIII в. Это понятие впервые ввёл Пётр I. Однако считается, что подобные вычисления начали применяться ещё в Смутное время — как результат первой в мировой истории привязки чеканных монет 1 к 100, когда рубль сначала состоял из 10 гривенников, а позже из 100 копеек.
Долгое время под процентами понимались исключительно прибыль или убыток на каждые 100 рублей. Проценты применялись только в торговых и денежных сделках. Затем область их применения расширилась.
Например, можно услышать фразы «в выборах приняли участие 60% избирателей», «успеваемость в классе 95%», «банк начисляет 12% годовых», «молоко содержит 1,5% жира», «материал состоит из 100% хлопка», «скидка составляет 5%», «на карту начисляется кэшбэк 3,5%» и так далее.
Современная жизнь делает задачи на проценты актуальными. Вопросы инфляции, девальвации, повышения цен, снижения покупательной способности касаются каждого человека. Школьники — будущие участники финансового рынка, налогоплательщики, вкладчики, заёмщики, поэтому уже на начальных ступенях образовательной системы необходимо вводить финансовое обучение.
Вполне закономерно, что каждый из нас хочет получать дополнительный доход. Банковские вклады (депозиты) — простой способ не только сохранить, но и приумножить свои сбережения. У всех банков разные процентные ставки, которые зависят от условий хранения денег: валюты, сроков, суммы размещения, возможности снятия и пополнения счёта, капитализации процентов.
Давайте разберёмся с понятием «процентная ставка по вкладу» и видами процентов.
Процентная ставка — это процент, который клиент получает за размещение средств на вкладе на определённый срок. Обычно подразумевается годовая процентная ставка. Если срок вклада больше или меньше года, для расчёта дохода необходимо привести ставку к реальному сроку вклада.
Однако выгода банковского вклада оценивается не только по процентной ставке. Большое влияние на доходность оказывает способ начисления процентов. В финансовой сфере существует понятие простого и сложного процента.
Простые проценты начисляются по следующей формуле:
Решение типовых задач
Задача 1.
Банк начисляет простой процент. Процентная ставка равна 20%. Вкладчик размещает на счете 1000000 руб. Определить, какая сумма будет получена по счету через 5 лет.
Решение:
Сумма, получающаяся через n лет при начислении простых процентов, вычисляется по формуле (1.1):
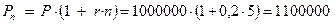 руб.
руб.
Задача 2.
Вкладчик размещает на счете 20000 руб. на четыре года. Банк начисляет простой процент. Процентная ставка за первый год равна 6%, второй – 8%, третий – 10%, четвертый – 12%. Определить, какая сумма будет получена по счету через 4 года.
Решение:
При начислении за каждый год разного процента формула (1.1) принимает вид:
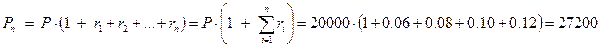 руб.
руб.
Задача 3.
Банк начисляет простой процент. Процентная ставка равна 7%. Вкладчик размещает на счете 5000 руб. на 180 дней. Определить, какая сумма будет получена по счету. Финансовый год (база) равен 365 дням.
Решение:
Расчеты производятся по формуле (1.2):
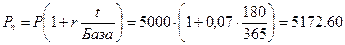 руб.
руб.
Задача 4.
Банк начисляет простой процент. Процентная ставка равна 10%. Вкладчик размещает на счете 50000 руб. на 9 месяцев. Определить, какая сумма будет получена по счету.
Решение:
Расчеты производятся по формуле (1.3):
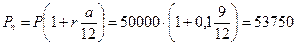 руб.
руб.
Задача 5.
Процентная ставка при временной базе 365 дней равна 10%. Определить эквивалентную ей ставку по базе 360 дней.
Решение:
Расчеты производятся по следующей формуле:
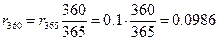 или 9.86% годовых.
или 9.86% годовых.
Задача 6.
Вкладчик размещает в банке 100000 руб. под 12% годовых. Банк осуществляет капитализацию процентов на счете в конце каждого года. Определить, какая сумма денег будет получена по счету через 6 лет.
Решение:
Расчеты производятся по формуле (1.4):
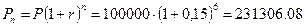 руб.
руб.
Задача 7.
Вкладчик размещает в банке 200000 руб. на три года. Капитализация процентов осуществляется ежегодно. За первый год банк начисляет 9%, второй – 7%, третий – 5% годовых. Определить, какая сумма денег получится на счете через три года.
Решение:
При начислении за каждый год разного процента формула (1.2) принимает вид:
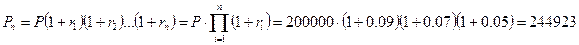 руб.
руб.
Задача 8.
Вкладчик размещает в банке 400000 руб. под 8.5% годовых. Банк осуществляет капитализацию процентов на счете ежемесячно. Определить, какая сумма денег получится на счете через три года.
Решение:
Расчеты производятся по формуле (1.5):
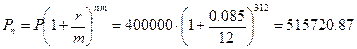 руб.
руб.
Задача 9.
В начале года вкладчик размещает в банке 500000 руб. под 9% годовых. Банк осуществляет капитализацию процентов а конце каждого года. В течение года по счету начисляется простой процент. Определить, какая сумма денег получится на счете через 4 года и 180 дней. База 365 дней.
Решение:
Расчеты производятся по формуле (1.9):
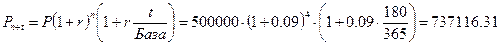 руб.
руб.
Задача 10.
Банк начисляет о счету 12% годовых. Капитализация процентов осуществляется ежемесячно. Определить величину эффективной процентной ставки.
Решение:
Расчеты производятся по формуле (1.7):
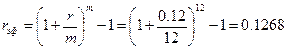 или 12.68% годовых.
или 12.68% годовых.
Задача 11.
Доходность финансового инструмента с погашением через 250 дней равна 12% годовых. Определить эффективную процентную ставку. База 365 дней.
Решение:
Расчеты производятся по формуле (1.34):
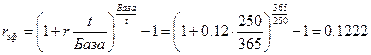 или 12.22% годовых.
или 12.22% годовых.
Задача 12.
В расчете на 90 дней доходность финансовой операции инвестора составила 7%. определить эффективную процентную ставку. База 365 дней.
Решение:
Для решения задачи преобразуем формулу (1.30) следующим образом:
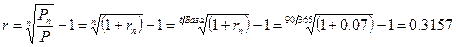 или 31.57% годовых.
или 31.57% годовых.
Задача 13.
Эффективная процентная ставка равна 9.6% годовых. Определить эквивалентную ей простую годовую процентную ставку, если начисление процентов осуществляется каждый месяц.
Решение:
Выразим из формулы (1.7) величину r:
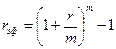 ð
ð 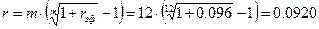 или 9.20% годовых.
или 9.20% годовых.
Задача 14.
Вкладчик размещает в банке 10000 руб. по 12% годовых. Процент начисляется непрерывно. Определить, какую сумму денег он получит на счете через 3 года.
Решение:
Расчеты производятся по формуле (1.6):
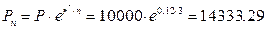 руб.
руб.
Задача 15.
Определить величину непрерывно начисляемого процента эквивалентного 11%, если капитализация процентов осуществляется ежеквартально.
Решение:
Расчеты производятся по формуле (1.8):
 или 10.85%.
или 10.85%.
Задача 16.
Непрерывно начисляемый процент равен 12%. Определить величину эквивалентного процента, начисляемого четыре раза в год.
Решение:
Выражая r из формулы (1.8) получаем:
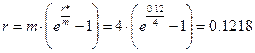 или 12.18% годовых.
или 12.18% годовых.
Задача 17.
Инвестор открывает в банке депозит на 3 года под 12% годовых (проценты простые) и хотел бы в конце периода получить по депозиту 50 тыс. руб. Определить, какую сумму ему следует разместить сегодня на счете.
Решение:
Расчеты производятся по формуле (1.13):
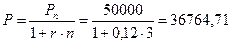 руб.
руб.
Задача 18.
Инвестор открывает в банке депозит на 200 дней под 11% годовых и хотел бы в конце периода получить по депозиту 40 тыс. руб. Определить, какую сумму ему следует разместить сегодня на счете. База 365 дней.
Решение:
Расчеты производятся по формуле (1.14):
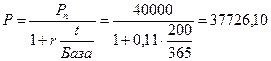 руб.
руб.
Задача 19.
Инвестор открывает в банке депозит на три года под 9% годовых и хотел бы в конце периода получить по депозиту 200 тыс. руб. Определить, какую сумму ему следует разместить сегодня на счете. Капитализация процентов проводится в конце каждого года.
Решение:
Расчеты производятся по формуле (1.10):
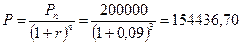 руб.
руб.
Задача 20.
Инвестор открывает в банке депозит на три года под 8% годовых и хотел бы в конце периода получить по депозиту 500 тыс. руб. Банк начисляет проценты ежемесячно. Определить, какую сумму ему следует разместить сегодня на счете.
Решение:
Расчеты производятся по формуле (1.11):
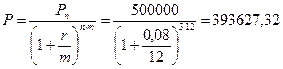 руб.
руб.
Задача 21.
Инвестор открывает в банке депозит на 100 дней и хотел бы в конце периода получить по депозиту 300 тыс. руб. По депозиту банк начисляет непрерывный процент в размере 9%. Определить, какую сумму ему следует разместить сегодня на счете. База 365 дней.
Решение:
Расчеты производятся по формуле (1.12):
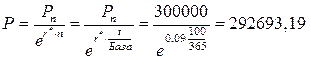 руб.
руб.
Задача 22.
Инвестор открывает в банке депозит под 11% годовых (простой процент) на сумму 250 тыс. руб. и хотел бы в конце периода получить по депозиту 300 тыс. руб. Определить на сколько дней следует открыть депозит. База 365 дней.
Решение:
Расчеты производятся по формуле (1.16):
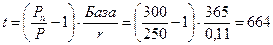 дня или 1 год и 299 дней.
дня или 1 год и 299 дней.
Задача 23.
В начале года инвестор открывает в банке депозит на сумму 100 тыс. руб. и хотел бы получить по счету 120 тыс. руб. Банк начисляет 8% годовых, капитализация процентов осуществляется в конце каждого года. Определить на какой период времени следует открыть депозит.
Решение:
Расчеты производятся по формуле (1.17):
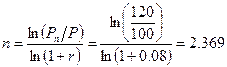 лет или 2 года 135 дней.
лет или 2 года 135 дней.
Задача 24.
В начале года инвестор открывает в банке депозит на сумму 1 млн. руб. и хотел бы получить по счету 1150000 руб. Банк начисляет 8% годовых, капитализация процентов осуществляется каждый квартал. Определить на какой период времени следует открыть депозит.
Решение:
Выразим из формулы (1.5) величину n:
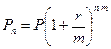 ð
ð 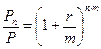 ð
ð 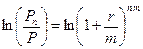 ð
ð 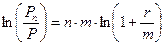 ð
ð
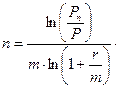
Подставим в полученную формулу числовые данные:
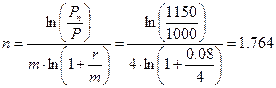 года или чуть больше чем 1 год и 3 квартала.
года или чуть больше чем 1 год и 3 квартала.
Задача 25.
В начале года инвестор открывает в банке депозит на сумму 1 млн. руб. и хотел бы получить по счету 1300000 руб. Банк начисляет 10% годовых. Процент начисляется непрерывно. Определить на какой период времени следует открыть депозит.
Решение:
Проведем преобразования формулы (1.6):
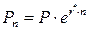 ð
ð 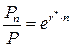 ð
ð 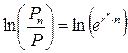 ð
ð 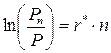 ð
ð 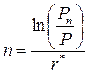 .
.
Подставим в полученную формулу числовые данные:
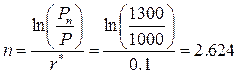 года или 2 года 228 дней.
года или 2 года 228 дней.
Задача 26.
Инвестор в течение трех лет в конце каждого года получает по 2000 руб. и размещает каждый платеж по 12% годовых до окончания четырехлетнего периода. Определить будущую стоимость аннуитета.
Решение:
Расчеты производятся по формуле (1.19):
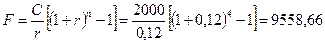 руб.
руб.
Задача 27.
Предприятие выпустило облигации с погашением через семь лет на сумму 10 млрд. руб. для погашения облигаций будет создан выкупной фонд. В выкупной фонд планируется ежегодно отчислять равные суммы средств, которые будут инвестироваться до момента погашения облигаций под 11% годовых. Определить размер ежегодных отчислений для формирования выкупного фонда.
Решение:
Расчеты производятся по формуле (1.20):
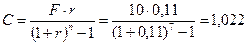 млрд. руб.
млрд. руб.
Задача 28.
Инвестору выплачивается пятилетний аннуитет. В расчете на год платеж составляет 20000 руб., однако платежи осуществляются каждый квартал. Инвестор размещает получаемые суммы по 12% годовых до истечения аннуитета. Определить будущую стоимость аннуитета.
Решение:
Расчеты производятся по формуле (1.22):
 руб.
руб.
Задача 29.
Инвестор в течение пяти лет в конце каждого года получает по 10000 руб. и размещает каждый платеж по 10% годовых до окончания пятилетнего периода. Проценты капитализируются ежеквартально. Определить будущую стоимость аннуитета.
Решение:
Расчеты производятся по формуле (1.24):
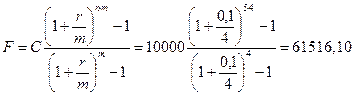 руб.
руб.
Задача 30.
Лицо А в течение следующих семи лет в конце каждого года должно выплачивать по своим обязательствам по 50 тыс. руб. Чтобы располагать данными деньгами к концу следующего года, оно решает сегодня открыть в банке семилетний депозит на некоторую сумму. По депозиту ежегодно начисляется 12%, средства со счета можно снимать полностью или частично в конце каждого года. Какую сумму следует сегодня разместить на депозите лицу А, чтобы за счет средств депозита покрыть все свои обязательства и, после очередного платежа на депозите больше не осталось денег.
Решение:
Сумма, которую лицо А должно разместить на депозите, равна приведенной стоимости аннуитета. Расчеты производятся по формуле (1.25):
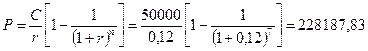 руб.
руб.
Задача 31.
Заемщик берет кредит на восемь лет в размере 10 млн. руб. под 18% годовых с условием погашения его равными суммами в конце каждого года. Проценты начисляются в конце каждого года на оставшуюся часть долга. Определить величину ежегодной выплаты по кредиту.
Решение:
Ежегодную сумму по кредиту, выплачиваемую равными частями, можно определить из формулы (1.25), выразив величину С:
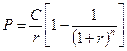 ð
ð 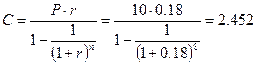 млн. руб.
млн. руб.
Задача 32.
Ежегодный платеж по шестилетнему аннуитету составляет 20000 руб. Он выплачивается равными суммами через каждый квартал и инвестируется под 12% годовых до истечения срока аннуитета. Проценты начисляются раз в год. Определить приведенную стоимость аннуитета.
Решение:
Расчеты производятся по формуле (1.26):
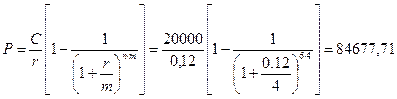 руб.
руб.
Задача 33.
Заемщик берет кредит на три года в размере 500 тыс. руб. под 18% годовых с условием погашения его равными суммами ежеквартально. Проценты по кредиту начисляются в конце каждого года. Определить величину ежеквартального платежа по кредиту.
Решение:
Из формулы (1.26) сумма ежегодного платежа определяется следующим образом:
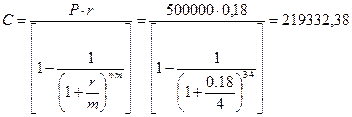 руб.
руб.
Ежеквартальный платеж равен:
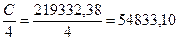 руб.
руб.
Задача 34.
Определить приведенную стоимость бессрочного аннуитета, по которому в конце каждого года выплачивается 3000 руб., если процентная ставка равна 10%.
Решение:
Расчеты производятся по формуле (1.28):
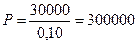 руб.
руб.
Задача 35.
Вкладчик инвестировал 50000 руб. и получил через 6 лет 150000. Определить, чему равна доходность инвестиций в расчете на пять лет.
Решение:
Расчеты производятся по формуле (1.29):
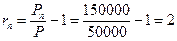 или 200% за 6 лет.
или 200% за 6 лет.
Задача 36.
Вкладчик инвестировал 60000 руб. и получил через 7 лет 170000. Определить, чему равна доходность инвестиций в расчете на год.
Решение:
Расчеты производятся по формуле (1.30):
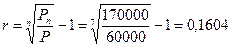 или 16.04% годовых.
или 16.04% годовых.
Задача 37.
Вкладчик инвестировал 20000 руб. и получил через 4 года 70000 руб. Процент по инвестициям начислялся ежеквартально. Определить, чему равна доходность инвестиций в расчете на год.
Решение:
Расчеты производятся по формуле (1.31):
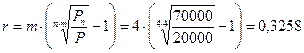 или 32.58% годовых.
или 32.58% годовых.
Задача 38.
Вкладчик инвестировал 15000 руб. и получил через 4 года 35000 руб. По инвестициям начислялся непрерывный процент. Определить, чему равна доходность инвестиций в расчете на год.
Решение:
Расчеты производятся по формуле (1.32):
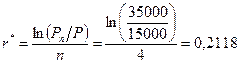 или 21.18% годовых.
или 21.18% годовых.
Задача 39.
Вкладчик разместил на счете в банке 12000 руб. и получил через 250 дней 13000 руб. По счету начислялся простой процент. Определить доходность его операции в расчете на год на основе простого процента. Финансовый год равен 365 дням.
Решение:
Расчеты производятся по формуле (1.33):
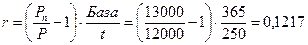 или 12.17 годовых.
или 12.17 годовых.
Задача 40.
Вкладчик разместил на счете в банке 11000 руб. и получил через 200 дней 12000 руб. По счету начислялся простой процент. Определить доходность его операции в виде эффективной процентной ставки. Финансовый год равен 365 дням.
Решение:
Подставим выражение для r из формулы (1.33) в формулу (1.34):
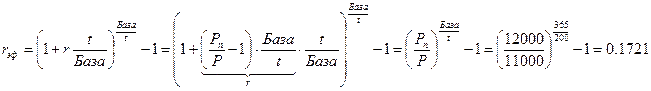
или 17.12% годовых.
Задача 41.
Инвестор разместил на банковском депозите 10000 руб. и через три года получил 14000 руб. Капитализация процентов осуществлялась ежегодно. За первый год банк начислил по счету 11%, за третий – 13%. Определить, какую ставку начислил банк за второй год.
Решение:
При начислении за каждый год разного процента формула сложных процентов имеет вид (см. задачу 7):
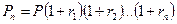
или для нашего случая:
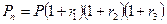 .
.
Откуда имеем:
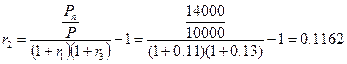 или 11.62% годовых.
или 11.62% годовых.
§
Простой процент
Задача 1.1.
Банк начисляет простой процент. Процентная ставка равна 10%. Вкладчик размещает на счете 1000 руб. Определить, какая сумма будет получена по счету через 5 лет.
Задача 1.2.
Банк начисляет простой процент. Процентная ставка равна 10%. Вкладчик размещает на счете 2000 руб. Определить, какая сумма будет получена по счету через 3 года.
Задача 1.3.
Вкладчик размещает на счете 2000 руб. на три года. Банк начисляет простой процент. Процентная ставка за первый год равна 8%, второй – 9%, третий – 10%. Определить, какая сумма будет получена по счету через 3 года.
Задача 1.4.
Банк начисляет простой процент. Процентная ставка равна 6%. Вкладчик размещает на счете 3000 руб. на 90 дней. Определить, какая сумма будет получена по счету. Финансовый год (база) равен 365 дням.
Задача 1.5.
Банк начисляет простой процент. Процентная ставка равна 8%. Вкладчик размещает на счете 4000 руб. на 180 дней. Определить, какая сумма будет получена по счету. База 360 дней.
Задача 1.6.
Банк начисляет простой процент. Процентная ставка равна 9%. Вкладчик размещает на счете 5000 руб. на 6 месяцев. Определить, какая сумма будет получена по счету.
Задача 1.7.
Процентная ставка при временной базе 365 дней равна 10%. Определить эквивалентную ей ставку по базе 360 дней.
Задача 1.8.
Процентная ставка при временной базе 360 дней равна 10%. Определить эквивалентную ей ставку по базе 365 дней.
Сложный процент. Эффективная ставка. Непрерывное начисление процентов.
Задача 1.9.
Вкладчик размещает в банке 1000 руб. под 10% годовых. Банк осуществляет капитализацию процентов на счете в конце каждого года. Определить, какая сумма денег будет получена по счету через 5 лет.
Задача 1.10.
Вкладчик размещает в банке 2000 руб. под 9% годовых. Банк осуществляет капитализацию процентов на счете в конце каждого года. Определить, какая сумма денег будет получена по счету через 3 года.
Задача 1.11.
Вкладчик размещает в банке 1000 руб. на три года. Капитализация процентов осуществляется ежегодно. За первый год банк начисляет 10%, второй – 9%, третий – 8% годовых. Определить, какая сумма денег получится на счете через три года.
Задача 1.12.
Вкладчик размещает в банке 1000 руб. под 9.5% годовых. Банк осуществляет капитализацию процентов на счете через каждые полгода. Определить, какая сумма денег получится на счете через три года.
Задача 1.13.
Вкладчик размещает в банке 2000 руб. под 8% годовых. Банк осуществляет капитализацию процентов на счете ежеквартально. Определить. какая сумма денег получится на счете через три года.
Задача 1.14.
В начале года вкладчик размещает в банке 2000 руб. под 8% годовых. Банк осуществляет капитализацию процентов а конце каждого года. В течение года по счету начисляется простой процент. Определить, какая сумма денег получится на счете через 3 года и 90 дней. База 365 дней.
Задача 1.15.
Банк начисляет о счету 10% годовых. Капитализация процентов осуществляется два раза в год. Определить величину эффективной процентной ставки.
Задача 1.16.
Банк начисляет о счету 10% годовых. Капитализация процентов осуществляется ежеквартально. Определить величину эффективной процентной ставки.
Задача 1.17.
Доходность финансового инструмента с погашением через 270 дней равна 10% годовых. Определить эффективную процентную ставку. База 365 дней.
Задача 1.18.
Доходность финансового инструмента с погашением через 50 дней равна 5.4% годовых. Определить эффективную процентную ставку. База 365 дней.
Задача 1.19.
В расчете на 80 дней доходность финансовой операции инвестора составила 10%. определить эффективную процентную ставку. База 365 дней.
Задача 1.20.
Банк предлагает три годичных депозита: 1) ставка 10% годовых, начисление процентов по завершении года; 2) ставка 9.9% капитализация процентов осуществляется ежеквартально; 3) ставка 9.8%, капитализация процентов осуществляется ежемесячно. Определить, какой депозит следует выбрать инвестору, если он планирует разместить деньги на год.
Задача 1.21.
Эффективная процентная ставка равна 8.16% годовых. Определить эквивалентную ей простую годовую процентную ставку, если начисление процентов осуществляется каждые полгода.
Задача 1.22.
Эффективная процентная ставка равна 8.77% годовых. Определить эквивалентную ей простую годовую процентную ставку, если начисление процентов осуществляется ежеквартально.
Задача 1.23.
Вкладчик размещает в банке 1000 руб. по 10% годовых. Процент начисляется непрерывно. Определить, какую сумму денег он получит на счете через 2 года.
Задача 1.24.
Вкладчик размещает в банке 1000 руб. по 10% годовых. Процент начисляется непрерывно. Определить, какую сумму денег он получит на счете через 5 лет.
Задача 1.25.
Вкладчик размещает в банке 1000 руб. по 10% годовых. Процент начисляется непрерывно. Определить, какую сумму денег он получит на счете через полгода.
Задача 1.26.
Определить величину непрерывно начисляемого процента эквивалентного 10%, начисляемым один раз в год.
Задача 1.27.
Определить величину непрерывно начисляемого процента эквивалентного 15%, начисляемым один раз в год.
Задача 1.28.
Определить величину непрерывно начисляемого процента эквивалентного 10%, если капитализация процентов осуществляется два раза в год.
Задача 1.29.
Определить величину непрерывно начисляемого процента эквивалентного 10%, если капитализация процентов осуществляется четыре раза в год.
Задача 1.30.
Непрерывно начисляемый процент равен 10%. Определить величину эквивалентного процента, начисляемого один раз в год.
Задача 1.31.
Непрерывно начисляемый процент равен 10%. Определить величину эквивалентного процента, начисляемого два раза в год.
Задача 1.32.
Непрерывно начисляемый процент равен 8%. Определить величину эквивалентного процента, начисляемого четыре раза в год.
Дисконтированная стоимость
Задача 1.33.
Инвестор открывает в банке депозит на один год под 10% годовых и хотел бы в конце периода получить по депозиту 10 тыс. руб. Определить, какую сумму ему следует разместить сегодня на счете.
Задача 1.34.
Инвестор открывает в банке депозит на два года под 10% годовых и хотел бы в конце периода получить по депозиту 10 тыс. руб. Определить, какую сумму ему следует разместить сегодня на счете.
Задача 1.35.
Инвестор открывает в банке депозит на два года под 10% годовых и хотел бы в конце периода получить по депозиту 10 тыс. руб. Банк начисляет проценты ежеквартально. Определить, какую сумму ему следует разместить сегодня на счете.
Задача 1.36.
Инвестор открывает в банке депозит на 90 дней под 10% годовых и хотел бы в конце периода получить по депозиту 10 тыс. руб. Определить, какую сумму ему следует разместить сегодня на счете. База 365 дней.
Задача 1.37.
Инвестор открывает в банке депозит на 90 дней и хотел бы в конце периода получить по депозиту 10 тыс. руб. По депозиту банк начисляет непрерывный процент в размере 10%. Определить, какую сумму ему следует разместить сегодня на счете. База 360 дней.
Определение периода начисления процентов
Задача 1.38.
Инвестор открывает в банке депозит под 10% годовых (простой процент) на сумму 10 тыс. руб. и хотел бы в конце периода получить по депозиту 10.5 тыс. руб. Определить на сколько дней следует открыть депозит. База 360 дней.
Задача 1.39.
В начале года инвестор открывает в банке депозит на сумму 10 тыс. руб. и хотел бы получить по счету 11881 руб. Банк начисляет 9% годовых, капитализация процентов осуществляется в конце каждого года. Определить на какой период времени следует открыть депозит.
Задача 1.40.
В начале года инвестор открывает в банке депозит на сумму 1 млн. руб. и хотел бы получить по счету 1092025 руб. Банк начисляет 9% годовых, капитализация процентов осуществляется каждые полгода. Определить на какой период времени следует открыть депозит.
Задача 1.41.
В начале года инвестор открывает в банке депозит на сумму 1 млн. руб. и хотел бы получить по счету 1141166 руб. Банк начисляет 9% годовых, капитализация процентов осуществляется каждые полгода. Определить на какой период времени следует открыть депозит.
Задача 1.42.
В начале года инвестор открывает в банке депозит на сумму 1 млн. руб. и хотел бы получить по счету 1271249.15 руб. Банк начисляет 8% годовых. Процент начисляется непрерывно. Определить на какой период времени следует открыть депозит.
Задача 1.43.
В начале года инвестор открывает в банке депозит на сумму 1 млн. руб. и хотел бы получить по счету 1342850.24 руб. Банк начисляет 8% годовых. Процент начисляется непрерывно. Определить на какой период времени следует открыть депозит. База 365 дней.
Аннуитет
Задача 1.44.
Инвестор в течение трех лет в конце каждого года получает по 1000 руб. и размещает каждый платеж по 10% годовых до окончания трехлетнего периода. Определить будущую стоимость аннуитета.
Задача 1.45.
Инвестор в течение пяти лет в конце каждого года получает по 1000 руб. и размещает каждый платеж по 9% годовых до окончания пятилетнего периода. Определить будущую стоимость аннуитета.
Задача 1.46.
Предприятие выпустило облигации с погашением через восемь лет на сумму 5 млрд. руб. для погашения облигаций будет создан выкупной фонд. В выкупной фонд планируется ежегодно отчислять равные суммы средств, которые будут инвестироваться до момента погашения облигаций под 10% годовых. Определить размер ежегодных отчислений для формирования выкупного фонда.
Задача 1.47.
Инвестору выплачивается пятилетний аннуитет. В расчете на год платеж составляет 1000 руб., однако платежи осуществляются через каждые полгода. Инвестор размещает получаемые суммы по 8% годовых до истечения аннуитета. Определить будущую стоимость аннуитета.
Задача 1.48.
Инвестору выплачивается восьмилетний аннуитет. В расчете на год платеж составляет 2000 руб., однако платежи осуществляются ежеквартально. Инвестор размещает получаемые суммы по 6% годовых до истечения аннуитета. Определить будущую стоимость аннуитета.
Приведенная стоимость аннуитета
Задача 1.49.
Ежегодный платеж по пятилетнему аннуитету составляет 1000 руб. и инвестируется под 10% годовых до истечения срока аннуитета. Определить приведенную стоимость аннуитета.
Задача 1.50.
Лицо А в течение следующих восьми лет в конце каждого года должно выплачивать по своим обязательствам по 20 тыс. руб. Чтобы располагать данными деньгами к концу следующего года, оно решает сегодня открыть в банке восьмилетний депозит на некоторую сумму. По депозиту ежегодно начисляется 9%, средства со счета можно снимать полностью или частично в конце каждого года. Какую сумму следует сегодня разместить на депозите лицу А, чтобы за счет средств депозита покрыть все свои обязательства и, после очередного платежа на депозите больше не осталось денег.
Задача 1.51.
Лицо А в течение следующих пяти лет в конце каждого года должно выплачивать лицу В по 30 тыс. руб. В результате переговоров А и В договорились о том, что А погасит свои обязательства единовременным платежом в начале периода. Сумма платежа должна быть такой, чтобы В, разместив деньги на счете в банке, могло обеспечить себе поступление средств, аналогичных выплатам по пятилетнему аннуитету. Определить сумму единовременного платежа, если по счету в банке ежегодно начисляется 8%, средства со счета можно снимать полностью или частично в конце каждого года.
Задача 1.52.
Заемщик берет кредит на десять лет в размере 5 млн. руб. под 15% годовых с условием погашения его равными суммами в конце каждого года. Проценты начисляются в конце каждого года на оставшуюся часть долга. Определить величину ежегодной выплаты по кредиту.
Задача 1.53.
Ежегодный платеж по пятилетнему аннуитету составляет 1000 руб. Он выплачивается равными суммами через каждые полгода и инвестируется под 10% годовых до истечения срока аннуитета. Определить приведенную стоимость аннуитета.
Задача 1.54.
Заемщик берет кредит на два года в размере 1 млн. руб. под 12% годовых с условием погашения его равными суммами ежеквартально. Определить величину ежеквартального платежа по кредиту.
Задача 1.55.
Определить приведенную стоимость бессрочного аннуитета, по которому в конце каждого года выплачивается 1000 руб., если процентная ставка равна 8%.
Доходность
Задача 1.56.
Вкладчик инвестировал 10000 руб. и получил через 5 лет 50000 руб. Определить, чему равна доходность инвестиций в расчете на пять лет.
Задача 1.57.
Вкладчик инвестировал 10000 руб. и получил через 5 лет 50000 руб. Определить, чему равна доходность инвестиций в расчете на год.
Задача 1.58.
Вкладчик инвестировал 10000 руб. и получил через 3 года 9500 руб. Определить, чему равна доходность инвестиций в расчете на год.
Задача 1.59.
Вкладчик инвестировал 10000 руб. и получил через 1.5 года 9500 руб. Определить, чему равна доходность инвестиций в расчете на год.
Задача 1.60.
Вкладчик инвестировал 10000 руб. и получил через 5 лет 50000 руб. Процент по инвестициям начислялся ежеквартально. Определить, чему равна доходность инвестиций в расчете на год.
Задача 1.61.
Вкладчик инвестировал 10000 руб. и получил через 5 лет 50000 руб. По инвестициям начислялся непрерывный процент. Определить, чему равна доходность инвестиций в расчете на год.
Задача 1.62.
Вкладчик инвестировал 10000 руб. и получил через три месяца 10800 руб. По инвестициям начислялся непрерывный процент. Определить, чему равна доходность инвестиций в расчете на год на основе непрерывно начисляемого процента.
Задача 1.63.
Вкладчик разместил на счете в банке 10000 руб. и получил через 180 дней 10540 руб. По счету начислялся простой процент. Определить доходность его операции в расчете на год на основе простого процента. Финансовый год равен 365 дням.
Задача 1.64.
Вкладчик разместил на счете в банке 10000 руб. и получил через 180 дней 10540 руб. По счету начислялся простой процент. Определить доходность его операции в виде эффективной процентной ставки. Финансовый год равен 365 дням.
Задача 1.65.
Инвестор разместил деньги на банковском депозите на шесть лет. Капитализация процентов осуществлялась ежегодно. Определить, какую ставку по депозиту начислял банк, если в конце периода капитал вкладчика увеличился в четыре раза.
Задача 1.66.
Инвестор разместил на банковском депозите 1000 руб. и через три года получил 1340 руб. Капитализация процентов осуществлялась ежегодно. За первый год банк начислил по счету 10%, за третий – 12%. Определить, какую ставку начислил банк за второй год.






