- (практическая). решение задач
- Анализ ликвидности баланса предприятия
- Задача №29.
- Задача №35.
- Задача №46.
- Задача №47.
- Задача №49.
- Задача №51.
- Задача №55.
- Задача №63.
- Задача №64.
- Задача №65.
- Задача №67.
- Задача №682 (расчет величины чистых денежных средств)
- Задача №70.
- Методы денежно-кредитной политики центрального банка
- Рынок ценных бумаг
(практическая). решение задач
Задача 3. Средний пробег автомобиля – 60 км в день. Среднее количество рабочих дней в месяце – 22. Расход бензина – 10,5 литра на 100 км пробега. Дисконт по пластиковой карте – 5%. Цена бензина – 29,50 руб./литр.
Рассчитайте эффект от использования пластиковой карты при проведении расчетов по горюче-смазочным материалам за год.
Решение:
60*22*12= 15840- км – кол-во км за год;
15840*(10,5/100)= 1663,2 л – расход бензина за год;
(1663,2*29,50)*0,95=46611,18р. – стоимость бензина за год с учетом дисконта;
(1663,2*29,50)= 49064,4 р. – стоимость бензина за год без учета дисконта.
Эффект от использования карты составляет 2453,22 р.
Задача 4. Кредит в размере 1,5 млн. руб. выдан на 1 год под 18 % годовых.
Определите сумму возврата.
Решение :
S=P*(1 R*n)
S=1500000*(1 0,18*1) = 1770000 р. – сумма возврата.
Задача 5. Через 350 дней с момента подписания контракта должна быть возвращена сумма 5 млн. руб., которая выдается по простой ставке 18 % годовых при точном числе дней в году. Продолжительность года – 366 дней.
Определите сумму процентных денег.
Решение:
S=P*(1 R*T/K)
P= S/(1 R*T/K)
P= 5000000/(1 0,17*350/365) = 4299175,5 р.- первоначальная сумма, взятая в банке;
5000000 -4299175,5 =700824,5 р.- процентные деньги.
Задача 6. Кредит в размере 2,5 млн. руб. выдан 12 марта до 25 декабря включительно под 17% годовых. Т точное = 288 дней; Т приближенное = 283 дня; К = 365 дней. Определите размер суммы возврата при точном и приближенном числе дней.
Решение:
S=P*(1 R*T/K)
S1= 5000000*(1 0,17*288/365)= 5670684,9 р. – размер наращен суммы при точном исчислении;
S2=5000000*(1 0,17*283/365)=5659041,1р. -размер наращенной суммы при приближенном исчислении;
5670684,9 -5659041,1 = 11643,8 р.- разница.
Задача 7. Кредит в размере 5 млн. руб. выдан в 2022 г. на 100 дней под 19 % годовых. Определить сумму возврата.
Решение:
S=P*(1 R*Т/К)
S=5000000*(1 0,19*100/365) = 15 780 822 р. – сумма возврата.
Задача 8. Строительная фирма по кредитному договору должна вернуть банку 10 млн. руб. через 300 дней. Кредит выдаётся под 20 % годовых. Определить сумму кредита.
Решение:
S=P*(1 R*T/K)
P= S/(1 R*T/K)
P= 10000000/(1 0,2*300/365)= 8588235 р.- первоначальная сумма, взятая в банке.
Задача 9. Размер займа – 1500 тыс. руб. под 25 % годовых на 1 год. Темп инфляции ожидается в размере 15 % годовых. Определить реальную процентную ставку, если кредитным договором не предусмотрена компенсация инфляционных потерь.
Решение:
S=P*(1 R*n)
S= 1500000*(1 0,25*1) = 1875000 р. – сумма возврата без учета инфляции
Кд = 1/(1 0,15)= 0,87
S = 1875000*0,87 = 1631250 р.- сумма возврата с учетом инфляции
(1631250-1500000)/1500000*100 = 8,75 % – реальная процентная ставка.
Задача 10. Кредит в размере 1 млн. руб. выдан на 200 дней под 19 % годовых с возвратом на условиях шарового платежа. Ожидается, что уровень инфляции составит 6 % за срок ссуды. При этом условиями кредитного договора предусмотрено обязательство заёмщика компенсировать банку инфляционные потери.
Определите:
1. процентную ставку с учетом инфляции.
2. погашенную сумму с учетом инфляции.
3. коэффициент наращения с учетом инфляции.
Решение:
200дн – 10%;
365дн – Х %;
Х = 365*10/200 = 18,25% – годовой ожидаемый темп инфляции;
18,25 19 = 37,25%- простая % ставка с учетом инфляции.
S=P*(1 R*T/K)
S= 10000000*(1 0,3725*200/365) = 12041096 р.;
12041096 /10000000 = 1,20- к-т наращения.
Задача 11. Кредит выдается 12 марта по простой процентной ставке, равной 25% годовых. Заемщик 25 декабря должен возвратить 5 млн. руб. Годовой уровень инфляции 13,5%. Временная база К=365 дней. При этом условиями кредитного договора предусмотрено обязательство заёмщика компенсировать банку инфляционные потери.
Определите:
1. Реальную ставку с учетом инфляции.
2. Сумму, выданную заемщику, с учетом инфляции.
3. Величину дисконта.
Решение:
S=P*(1 R*T/K)
P= S/(1 R*T/K)
P= 5000000/(1 0,25*288/365)= 4176201,37 р.- сумма, выданная заёмщику без учета инфляции
13,5 * 289/365=10,689 %- инфляция;
Кд = 1/(1 0,10689) = 0,90343;
S = 4176201,37 *0,90343 = 3772905,6 р.- наращенная сумма с учетом инфляции;
Sпереплаты = 5000000 -3772905,6 = 1227094,396 р.
(1227094,396 /3772905,6) *100 = 32,52 % (за 289 дней)- реальная ставка;
РПСi= 32,52*365/289= 41,08 %.
Задача 12. Фирма приобрела в банке вексель, по которому через год должна получить 6,5 млн. руб. (номинальная стоимость векселя). В момент приобретения цена векселя составила 5,8 млн. руб. Определите доходность этой сделки. Решение:
(6500000-5800000)/5800000 = 0,12068*100=12,07 %- доходность сделки.
Задача 13. Определите доходность векселя сроком обращения 6 месяцев, если номинал векселя 15 млн. руб., а текущая цена продажи 14,5 млн. руб.
Задача 13. Определите доходность векселя сроком обращения 6 месяцев, если номинал векселя 3 млн. руб., а текущая цена продажи 2,8 млн. руб.
Решение:
Ставка процента в годовом выражении=(360/срок до погашения)*(курс пог.-курс пок.)/курс пок.
Ставка процента в годовом выражении:
(360/180)*(15000000-14500000)/14500000 = 0,0689*100=6,9%.
Задача 14. Первоначальная сумма депозита составляет 1,5 млн. руб.
Определите сумму вклада через 2 года при использовании простой и сложной ставки процентов, равной 12,5 % годовых.
Решение:
Метод сложных процентов:
1500000*(1 0,125) = 1687500 р. – сумма денег на конец 1-го года;
1687500*(1 0,125) = 1898438 р. – сумма депозита на конец 2-го года .
Метод простых процентов:
S= P*(1 R*n);
S= 1500000*(1 0,125*2) = 1875000 – наращенная сумма.
Задача 15. Какова доходность к погашению 180 – дневного векселя (в годовом исчислении) номиналом 1500 тыс. руб., если он был приобретен за 1440 тыс. руб.?
Решение:
Ставка процента в годовом выражении:
(360/срок до погашения)*(курс пог.-курс пок.)/курс пок.
Ставка процента в годовом выражении:
(360/180)*(1500000-1440000)/1440000 = 8,33%.
Задача 16. Какова ставка процента в годовом выражении по 90 – дневному векселю номиналом 10 млн. руб., приобретенному в момент выпуска по 9,8 млн. руб.?
Задача 16. Какова ставка процента в годовом выражении по 90 – дневному векселю номиналом 10 млн. руб., приобретенному в момент выпуска по 9,5 млн. руб.?
Решение:
Ставка процента в годовом выражении =(365/срок до погашения)*(курс пог.-курс пок.)/курс пок.
Ставка процента в годовом выражении:
(365/90)*(10000000-9800000)/9800000 = 9,16%.
Задача 17. Малое строительное предприятие приобрело автопогрузчик стоимостью 1280 тыс. руб. Годовая норма амортизации – 12%. В целях создания финансовых условий для ускорения внедрения в производство научно-технических достижений и повышение заинтересованности предприятий в ускорении обновления и технического развития активной части основных средств (машин, оборудования, транспортных средств) субъект малого предпринимательства вправе применить ускоренный метод начисления амортизации основных производственных фондов с отнесением начисленной суммы на издержки производства (обращения) в размере, в два раза превышающем нормы, установленные для соответствующих видов основных средств. Наряду с применением механизма ускоренной амортизации данные предприятия могут списывать дополнительно как амортизационные отчисления до 50% первоначальной стоимости основных средств со сроком службы более 3-х лет.
Задача 17. Малое строительное предприятие приобрело автопогрузчик стоимостью 1250 тыс. руб. Годовая норма амортизации – 12%. Рассчитайте: сумму списания на себестоимость амортизационных отчислений за каждый год их эксплуатации ускоренным методом; срок амортизации приобретенного оборудования.
Рассчитайте:
1)сумму списания на себестоимость амортизационных отчислений за каждый год их эксплуатации;
2)срок амортизации приобретенного оборудования.
Решение:
А = 1280000*(12*2)/100 1280000*50/100 = 947200 р. – отчисления в 1-й год эксплуатации;
1280000*(12*2)/100=3072000р. – отчисления во 2-й и 3-й год эксплуатации;
1280000 – 947200 – 3072000=256000р.;
1280000*0,02=256000р.;
2% – процент амортизации.
Задача 18. Акция имеет номинальную, курсовую стоимость и рыночную цену. Цена акции, обозначенная на ней, называется номиналом акции. Цена, по которой реально покупается акция, называется рыночной, она зависит от курсовой стоимости и курса акции. Курс акции находится в прямой зависимости от размера получаемого по ней дивиденда и в обратной зависимости от уровня ссудного (банковского) процента. Рассчитайте курс акции и ее курсовую стоимость по следующим исходным данным: номинальная цена акции 30 тыс. руб., дивиденд-55%, ссудный процент-18%.
Решение:
30000*55/100 = 91670 р. – курсовая стоимость акции;
55/18*100 = 305,6% – курс акции .
Задача 19. Прибыль акционерного общества, оставшаяся после всех отчислений и предназначенная на выплату дивидендов, составила за год 12 млн. руб. Общая сумма акций 25 млн. руб., в том числе привилегированных акций – 15 млн. руб. с фиксированным размером дивиденда – 50 % к номинальной стоимости.
Определите:
1. годовую сумму дивидендов по привилегированным акциям;
2. размер и ставку дивидендов по обыкновенным акциям;
3. средний размер и ставку дивидендов по всем акциям.
Решение:
15000000 * 0,5 = 7500000р .- годовая сумма дивидендов по привилегированным акциям;
12000000-7500000 = 4500000 р.- размер дивидендов по обыкновенным акциям;
(4500000/(25000000-15000000))*100 = 45% – ставка дивидендов по обыкновенным акциям;
(12000000/25000000)*100 = 48% – ставка дивидендов по всем акциям.
Задача 20. Рассчитайте балансовую стоимость акции акционерного общества закрытого типа, если: сумма активов АО – 15 млн. руб., сумма долгов 3,5 млн. руб., количество оплаченных акций – 250 шт.
Решение:
Балансовая стоимость = (15000000-3500000)/250 = 46000 р.
Задача 21. Прибыль акционерного общества, направленная на выплату дивидендов составляет 15 млн. руб. Количество акций в обращении 1 тыс. шт. номиналом 1000 руб., из них привилегированных 40%, с объявленным уровнем дивидендов 90% к их номинальной цене. Рассчитайте размер дивидендов по привилегированным и простым акциям и ставку дивидендов по простым акциям.
Решение:
1) 1000*40% = 400 шт. – количество привилегированных акций в обращении;
2) 100-400 = 600 шт. – количество простых акций в обращении;
3) 400*1000*90/100 = 360000 р. – дивиденды по привилегированным акциям;
4) 15000000 – 360000 = 14640000 р. – дивиденды по простым акциям;
5) 14640000 /600 = 24400 р. – дивиденды на 1 шт. простых акций;
6) (24400/1000)*100 = 2440%.
Задача 22. Чистая прибыль акционерного общества 20 млн. руб.; коэффициент выплаты дивидендов 0.1, количество акций в обращении 1000 шт., их них привилегированных 40%, номинальная цена акции – 1000 руб. Объявленный уровень дивидендов по привилегированным акциям 80% к их номинальной цене. Рассчитайте размер дивидендов по акциям.
Решение:
1) 20000000*0,1 = 2000000 р. – деньги на выплату дивидендов.
2) 1000*40% = 400 шт. – количество привилегированных акций в обращении
3) 400*1000*80/100 = 320000 р. – размер дивидендов по привилегированным акциям
4) 2000000-320000 =1680000 р. – размер дивидендов по простым акциям.
Задача 23. Коммерческий банк предоставил малому предприятию кредит в сумме 10 млн. руб. Процентная ставка составляет ј ставки рефинансирования ЦБ РФ, равной 8,5 % годовых. Срок погашения кредита – 6 месяцев.
Задание:
1). Рассчитать льготную ставку.
2). Сравнить варианты погашения кредита двумя способами:
а) сумма кредита и проценты будут погашены в конце срока шаровым платежом;
б) кредит и проценты по нему будут выплачиваться ежемесячно дифференцированными платежами.
Решение:
1) 8,5/4 = 2,125%
2) S= 10 * (1 0,02125*6/12) = 10,10625 млн. р. – шаровым платежом
3) Si = K Пi
K(const) = 10000000/6 = 1666667 р.
П1 = 10000000*0,02125/12 = 17708,33 р.
S1 = 1666667 17708,33 = 1684375,33 р. – взнос за 1-й месяц;
П2 = (10000000-1666667)*0,02125/12 = 14756,94 р.
S2 = 1666667 14756,94 = 1681423,9 р. – взнос за 2-й месяц;
П3 = (10000000-2*1666667)*0,02125/12 = 11805,56 р.
S3 = 1666667 11805,56 = 1678472,6 р. – взнос за 3-й месяц;
П4 = (10000000-3*1666667)*0,02125/12 = 8854,16 р.
S4 = 1666667 8854,16 = 1675521,2 р. – взнос за 4-й месяц ;
П5 = (10000000-4*1666667)*0,02125/12 = 5902,78 р.
S5 = 1666667 5902,78 = 1672569,78 р. – взнос за 5-й месяц;
П6 = (10000000-5*1666667)*0,02125/12 = 2951,39 р.
S6 = 1666667 2951,39 = 1669618,39 р. – взнос за 6-й месяц;
Si = 10061981 р. – дифференцированными платежами.
Вывод: при дифференцированных платежах плательщик экономит 44269р.
Задача 24. Предприятие приобретает пакет облигаций с фиксированной ставкой дохода 25 % годовых. Срок погашения облигаций – 2 года. По какой цене (в % от номинала) необходимо приобрести облигации, если предприятие планирует обеспечить себе доходность от финансовой сделки:
1). 55 % за 2 года
2). 55 % ежегодно.
Решение:
1) 100-(55-25*2)=95%;
2) 2)100-(55*2-25*2)=40%.
Задача 25. Инвестор располагает свободным капиталом в сумме 200 тыс. руб. и желает положить эту сумму в банк на депозит сроком на 2 года. Один коммерческий банк предлагает ежегодное начисление процентов из расчета 12 % годовых при условии капитализации доходов. Второй коммерческий банк предлагает ежеквартальное начисление процентов из расчета 12 % годовых при условии капитализации доходов. Какой из вариантов следует предпочесть инвестору?
Решение:
S1 = 200000*(1 0,12)І = 250880 р.;
S2 = 200000*(1 0,12*1/4)^8 = 253354 р.
Вывод: инвестору лучше предпочесть второй вариант с выгодой 2474 р.
Задача 26. Рассчитать второй вариант при условии ежемесячного начисления процентов (11,5% годовых).
Решение:
S2 = 200000*(1 0,115*1/12) ^24 = 251440 р.
Задача 27. Выручка от реализации продукции к концу первого и второго года реализации проекта в постоянных ценах (при отсутствии инфляции) составит соответственно 100 и 120 денежных единиц. Та же выручка в переменных ценах (за счет инфляции) составит соответственно 125 и 170 денежных единиц. Определите номинальный и реальный индексы роста выручки за рассматриваемый период.
Решение:
120/100 = 1,2 (120%) -номинальный индекс роста;
170/125 = 1,36 (136%) -реальный индекс роста.
Задача 28. Проект предусматривает получение кредита в размере 10 млн. руб. в начале года под 20 % годовых сроком на 1 год. Ожидаемый уровень инфляции за год принят в размере 12 %. Условия возврата – шаровый платёж.
Определить реальную процентную ставку при условии, что кредитным договором не предусмотрена компенсация инфляционных потерь.
Решение:
S= P*(1 R*n);
S= 10*(1 0,2*1) = 12000000р.- наращенная сумма без учета инфляции;
Кд = 1/(1 0,12) = 0,892857142;
S=12*0,892857142=10714285,71р.-наращенная сумма с учетом инфляции;
Переплата = 714285,71 р.
РПС = (714285,71/10000000)*100 = 7,14%.
Задача 29. Пусть время работы машины до полного износа – 50 тыс. часов, стоимость ее приобретения – 2,5 млн. руб., а ликвидационное сальдо (стоимость металлолома за вычетом затрат на демонтаж) – 250 тыс. руб. Определите норму амортизации машины по методу увязки с производительностью и сумму амортизации за 1 год, если за этот период время работы машины составило 950 часов.
Решение:
Износ за весь срок службы = Первон. стоимость – ликвид. стоимость
2,5 – 0,25 = 2,25 млн. р. – износ за весь срок службы;
ОФ = 2250/50 = 45 р./час- норма амортизации;
45 * 950 = 42750 р.- амортизация за год.
Задача 30. Определите размеры амортизации и остаточной стоимости машины методом уменьшающегося остатка. Срок службы машины – 5 лет, Норма амортизации вдвое больше равномерной, рассчитанной методом линейной амортизации.
Год | Первоначальная стоимость, тыс.руб. | Остаточная стоимость на начало года | Норма амортизации, % | Сумма амортизации, тыс.руб. | Накопленная амортизация на конец года, тыс.руб. | Остаточная стоимость на конец года, тыс.руб. |
1 | 3500 | 3500 | 40 | 1400 | 1400 | 2100 |
2 | 2100 | 40 | 840 | 2240 | 1260 | |
3 | 1260 | 40 | 504 | 2704 | 756 | |
4 | 756 | 40 | 302,4 | 3006,4 | 453,6 | |
5 | 453,6 | 40 | 181,44 | 3187,84 | 312,16 |
Анализ ликвидности баланса предприятия
Ликвидность баланса — это степень покрытия обязательств предприятия активами, срок превращения которых в денежные средства соответствует сроку погашения обязательств. От степени ликвидности баланса зависит платежеспособность предприятия. Основной признак ликвидности — формальное превышение стоимости оборотных активов над краткосрочными пассивами. И чем больше это превышение, тем более благоприятное финансовое состояние имеет предприятие с позиции ликвидности.
Актуальность определения ликвидности баланса приобретает особое значение в условиях экономической нестабильности, а также при ликвидации предприятия вследствие его банкротства. Здесь встает вопрос: достаточно ли у предприятия средств для покрытия его задолженности. Такая же проблема возникает, когда необходимо определить, достаточно ли у предприятия средств для расчетов с кредиторами, т.е. способность ликвидировать (погасить) задолженность имеющимися средствами.
В данном случае, говоря о ликвидности, имеется в виду наличие у предприятия оборотных средств в размере, теоретически достаточном для погашения краткосрочных обязательств.
Для проведения анализа ликвидности баланса предприятия статьи активов группируют по степени ликвидности — от наиболее быстро превращаемых в деньги к наименее. Пассивы же группируют по срочности оплаты обязательств. Типичная группировка представлена в нижеприведенной таблице:
Таблица. Группировка активов и пассивов баланса для проведения анализа ликвидности
| Активы | Пассивы | ||||||
| Название группы | Обозначение | Состав | Название группы | Обозначение | Состав | ||
| Баланс до 2022г. | Баланс с 2022г. | Баланс до 2022г. | Баланс с 2022г. | ||||
| Наиболее ликвидные активы | А1 | стр. 260 250 | стр. 1250 1240 | Наиболее срочные обязательства | П1 | стр. 620 630 | стр. 1520 |
| Быстро реализуемые активы | А2 | стр. 240 270 | стр. 1230 | Краткосрочные пассивы | П2 | стр. 610 650 660 | стр. 1510 1540 1550 |
| Медленно реализуемые активы | А3 | стр. 210 220 — 216 | стр. 1210 1220 1260 — 12605 | Долгосрочные пассивы | П3 | стр. 590 | стр. 1400 |
| Трудно реализуемые активы | А4 | стр. 190 230 | стр. 1100 | Постоянные пассивы | П4 | стр. 490 640 — 216 | стр. 1300 1530 — 12605 |
| Итого активы | ВА | Итого пассивы | ВР | ||||
А.Д. Шеремет указывает на необходимость вычесть расходы, не перекрытые средствами фондов и целевого финансирования, и суммы расчетов с работниками по полученным ими ссудам. Расходы, не перекрытые средствами фондов и целевого финансирования, а также превышение величины расчетов с работниками по полученным ими ссудам над величиной ссуд банка, обусловленная выдачей ссуд работникам за счет средств специальных фондов организации, сокращается при вычитании иммобилизации из величины источников собственных средств. В случае обнаружения в ходе внутреннего анализа иммобилизации по статьям прочих дебиторов и прочих активов на ее величину также уменьшается итог быстрореализуемых активов. (А.Д. Шеремет. Комплексный анализ хозяйственной деятельности).
Для оценки ликвидности баланса с учетом фактора времени необходимо провести сопоставление каждой группы актива с соответствующей группой пассива.
1) Если выполнимо неравенство А1 > П1, то это свидетельствует о платежеспособности организации на момент составления баланса. У организации достаточно для покрытия наиболее срочных обязательств абсолютно и наиболее ликвидных активов.
2) Если выполнимо неравенство А2 > П2, то быстро реализуемые активы превышают краткосрочные пассивы и организация может быть платежеспособной в недалеком будущем с учетом своевременных расчетов с кредиторами, получения средств от продажи продукции в кредит.
3) Если выполнимо неравенство А3 > П3 , то в будущем при своевременном поступлении денежных средств от продаж и платежей организация может быть платежеспособной на период, равный средней продолжительности одного оборота оборотных средств после даты составления баланса.
Выполнение первых трех условий приводит автоматически к выполнению условия: A4<=П4
Выполнение этого условия свидетельствует о соблюдении минимального условия финансовой устойчивости организации, наличия у нее собственных оборотных средств.
На основе сопоставления групп активов с соответствующими группами пассивов выносится суждение о ликвидности баланса предприятия.
Сопоставление ликвидных средств и обязательств позволяет вычислить следующие показатели:
- текущая ликвидность, которая свидетельствует о платежеспособности ( ) или неплатежеспособности (-) организации на ближайший к рассматриваемому моменту промежуток времени: А1 А2=>П1 П2; А4<=П4
- перспективная ликвидность — это прогноз платежеспособности на основе сравнения будущих поступлений и платежей: А3>=П3; А4<=П4
- недостаточный уровень перспективной ликвидности: А4<=П4
- баланс не ликвиден:А4=>П4
Однако следует отметить, что проводимый по изложенной схеме анализ ликвидности баланса является приближенным, более детальным является анализ платежеспособности при помощи финансовых коэффициентов.
1. Коэффициент текущей ликвидности показывает, достаточно ли у предприятия средств, которые могут быть использованы им для погашения своих краткосрочных обязательств в течение года. Это основной показатель платежеспособности предприятия. Коэффициент текущей ликвидности определяется по формуле:
К = (А1 А2 А3) / (П1 П2)
В мировой практике значение этого коэффициента должно находиться в диапазоне 1-2. Естественно, существуют обстоятельства, при которых значение этого показателя может быть и больше, однако, если коэффициент текущей ликвидности более 2-3, это, как правило, говорит о нерациональном использовании средств предприятия. Значение коэффициента текущей ликвидности ниже единицы говорит о неплатежеспособности предприятия.
2. Коэффициент быстрой ликвидности, или коэффициент «критической оценки», показывает, насколько ликвидные средства предприятия покрывают его краткосрочную задолженность. Коэффициент быстрой ликвидности определяется по формуле:
К = (А1 А2) / (П1 П2)
В ликвидные активы предприятия включаются все оборотные активы предприятия, за исключением товарно-материальных запасов. Данный показатель определяет, какая доля кредиторской задолженности может быть погашена за счет наиболее ликвидных активов, т. е. показывает, какая часть краткосрочных обязательств предприятия может быть немедленно погашена за счет средств на различных счетах, в краткосрочных ценных бумагах, а также поступлений по расчетам. Рекомендуемое значение данного показателя от 0,7-0,8 до 1,5.
3. Коэффициент абсолютной ликвидности показывает, какую часть кредиторской задолженности предприятие может погасить немедленно. Коэффициент абсолютной ликвидности рассчитывается по формуле:
К = А1 / (П1 П2)
Показывает, какая часть краткосрочных обязательств может быть немедленно погашена за счет средств на различных счетах, в краткосрочных ценных бумагах, а также поступлений по расчетам с дебиторами. Значение данного показателя не должно опускаться ниже 0,2.
4. Для комплексной оценки ликвидности баланса в целом рекомендуется использовать общий показатель ликвидности баланса предприятия, который показывает отношение суммы всех ликвидных средств предприятия к сумме всех платежных обязательств (краткосрочных, долгосрочных, среднесрочных) при условии, что различные группы ликвидных средств и платежных обязательств входят в указанные суммы с определенными весовыми коэффициентами, учитывающими их значимость с точки зрения сроков поступления средств и погашения обязательств. Общий показатель ликвидности баланса определяется по формуле:
К = (А1 0,5*А2 0,3*А3) / (П1 0,5*П2 0,3*П3)
Оценивает изменения финансовой ситуации в компании сточки зрения ликвидности. Данный показатель применяется при выборе надежного партнера из множества потенциальных партнеров на основе финансовой отчетности. Значение данного коэффициента должно быть больше или равно 1.
5. Коэффициент обеспеченности собственными средствами показывает, насколько достаточно собственных оборотных средств у предприятия, необходимых для его финансовой устойчивости. Он определяется:
K = (П4 — А4) / (А1 А2 А3)
Значение данного коэффициента должно быть больше или равно 0,1.
6. Коэффициент маневренности функционального капитала показывает, какая часть функционирующего капитала заключена в запасах. Если этот показатель уменьшается, то это является положительным фактом. Он определяется из соотношения:
K = А3 / [(А1 А2 А3) — (П1 П2)]
В ходе анализа ликвидности баланса каждый из рассмотренных коэффициентов ликвидности рассчитывается на начало и конец отчетного периода. Если фактическое значение коэффициента не соответствует нормальному ограничению, то оценить его можно по динамике (увеличение или снижение значения).
Следует отметить, что в большинстве случаев достижение высокой ликвидности противоречит обеспечению более высокой прибыльности. Наиболее рациональная политика состоит в обеспечении оптимального сочетания ликвидности и прибыльности предприятия.
Наряду с приведенными показателями для оценки состояния ликвидности можно использовать показатели, основанные на денежных потоках:
- чистый денежный поток (NCF — Net Cash Flow);
- денежный поток от операционной деятельности (CFO — Cash Flow from Operations);
- денежный поток от операционной деятельности, скорректированный на изменения оборотного капитала (OCF — Operating Cash Flow);
- денежный поток от операционной деятельности, скорректированный на изменения оборотного капитала и удовлетворения потребности в инвестициях (OCFI — Operating Cash Flow after Investments);
- свободный денежный поток (FCF — Free Cash Flow).
При этом независимо от стадии жизненного цикла, на котором находится предприятие, менеджмент вынужден решать задачу определения оптимального уровня ликвидности, поскольку, с одной стороны, недостаточная ликвидность активов может привести как к неплатежеспособности, так и к возможному банкротству, а с другой стороны, избыток ликвидности может привести к снижению рентабельности. В силу этого современная практика требует появления все более совершенных процедур проведения анализа и диагностики состояния ликвидности.
Задача №29.
Компания намерена получить заем в 10 млн дат. крон на один год под фиксированную ставку 4% годовых. Но имеется возможность получить кредит только под «плавающую» ставку.
Компания может взять кредит в долларах США на международном рынке под 3% годовых, купить кроны на полученные доллары «на споте» и продать кроны за доллары по форварду на один год.
Сколько нужно взять долларов США в кредит и по какому форвардному курсу компании выгодно продать кроны за доллары США, если курс спот на момент получения долларового кредита равен 5 дат. крон за 1 долл. США?
Решение:
Если 1 долл. = 5,8323 дат. крон, то компании нужно взять в кредит 1 714 589,4 долл. (10 000 000 : 5,8323). Продав 1 714 589,4 долл. США на споте, компания получит искомые 10 млн дат. крон.
При ставке 3% годовых для погашения через год кредита в долларах США компании потребуется в конце года 1 766 027 долл. США (1714 589,4 х 1,03).
При ставке 4% годовых компании для погашения кредита в 10 млн крон в конце года понадобилось бы 10 400 ООО дат. крон (10 000 000 х 104%). Следовательно, компании будет выгодно продать кроны по форвардному курсу 5,8889 крон за 1 долл. (10 400 000 : : 1 766 027).
Задача №35.
В табл. 4.9 приведены данные о структуре и динамике обязательств банка. Требуется:
1) дать характеристику приведенной динамики и структуры обязательств коммерческого банка;
2) определить удельный вес отдельных статей обязательств в пассиве коммерческого банка;
3) определить отклонение обязательств от предыдущего периода;
4) сделать выводы.
Решение:
Приведем в табл. 4.10 данные о динамике и структуре обязательств.
Приведенные расчеты свидетельствуют о том, что при общем увеличении суммы обязательств банка его ресурсная база значительно ухудшилась вследствие существенного снижения средств на расчетных счетах клиентов и оттока средств населения. Значительную часть ресурсов банк привлек с межбанковского рынка от банков-резидентов.
Однако не следует забывать, что подобный рост ресурсов не может иметь долговременный характер, так как эти они могут быть использованы лишь для поддержания ликвидности на краткосрочный период. Кроме того, прирост обязательств за счет этого источника существенно повышает стоимость пассивов банка, поскольку межбанковские ресурсы относятся к наиболее дорогим пассивам. Поэтому банку следует расширить свою клиентскую базу.
Задача №46.
На вторичных торгах 26 апреля 2000 г. курс ГКО № 21139RMFS9 составлял 98,68%, курс ОФЗ-ПД № 25021RMFS5 -91,5%; курс ОФЗ-ФД № 27001RMFS5 — 78,99%. Надо определить:
1) в какие ценные бумаги инвестиции будут наиболее эффективными с точки зрения доходности к погашению (доходность рассчитать с учетом простой и сложной процентной ставки; данные по купонным облигациям следует взять из предыдущих задач; параметры ГКО № 21139RMFS9: номинал 1000 руб.; погашение 31 мая 2000 г.);
2) текущую (фактическую) доходность для купонных облигаций при условии, что цены аукционов соответствующих облигаций составляют: ОФЗ-ПД № 25021 RMFS5—80%; ОФЗ-ФД № 27001 RMFS5-70%.
Решение:
- Рассчитаем доходность к погашению по ГКО № 21139RMFS9, исходя из сложной и простой процентной ставки:
где
Простая ставка:
Сложная ставка:
- Рассчитаем доходность к погашению по ОФЗ-ПД № 25021RMFS5, исходя из сложной и простой процентной ставки:
где
Простая ставка:
Сложная ставка:
Отсюда находим 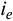
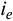
- Рассчитаем доходность к погашению по ОФЗ-ФД № 27001RMFS5, исходя из сложной и простой процентной ставки:
где
Простая ставка:
Сложная ставка: расчет эффективной доходности к погашению (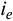
Таким образом, наибольшей доходностью обладают инвестиции в ОФЗ-ФД № 27001RMFS5. Данное обстоятельство легко объяснимо, ведь чем больше срок инвестирования, тем больше должна быть доходность инвестиционного инструмента.
- Рассчитаем текущую доходность купонных облигаций:
Задача №47.
Есть две государственные облигации ОФЗ-ФД: серии 27001RMFS5 и серии 27011RMFS4. На вторичных торгах 26 апреля 2000 г. курс этих облигаций составлял 78,99 и 61,4% соответственно. Основные показатели ОФЗ-ФД № 27001RMFS5 надо взять из предыдущих задач. Параметры ОФЗ-ФД № 27011RMFS4 указаны в табл. 6.3. Номинал 10 руб. Требуется:
1) найти среднерыночную доходность к погашению по представленным ценным бумагам;
2) определить дюрацию, модифицированную дюрацию и коэффициент Маколи (как изменится курс каждой облигации при изменении рыночночной доходности на 1%).
Решение:
- Произведем расчет доходности к погашению по ОФЗ-ФД № 2701 1RMFS4:
Расчет эффективной доходности к погашению (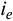
Эффективная доходность к погашению для ОФЗ-ФД № 27001RMFS5 равна 41,67% (задача 3, п. 3).
- Рассчитаем среднерыночную процентную ставку:
- Рассчитаем дюрацию и коэффициент Маколи для каждой облигации:
Таким образом, дюрация ОФЗ-ФД № 27011RMFS4 больше, чем дюрация ОФЗ-ФД № 27001RMFS5. Следовательно, первая облигация более чувствительна к изменению процентных ставок и обладает повышенным уровнем процентного риска.
Задача №49.
Надо рассчитать доходность портфеля, состоящего из государственных облигаций следующих типов: ГКО № 21139RMFS9 — 1000 шт; ОФЗ-ПД № 25021RMFS5 — 2000 шт; ОФЗ-ФД № 27001RMFS5 — 100 000 шт.
На вторичных торгах 26 апреля 2000 г. курс этих облигаций составил соответственно 98,68; 91,5 и 78,99%.
Решение:
Рассчитаем доходность к погашению по ГКО № 21139RMFS9, исходя из сложной и простой процентной ставки (данные взяты из задачи 3).
Простая ставка:
Сложная ставка:
Рассчитаем доходность к погашению по ОФЗ-ПД № 25021RMFS5, исходя из сложной и простой процентной ставки (данные взяты из задачи 3).
Простая ставка:
Сложная ставка:
Рассчитаем доходность к погашению по ОФЗ-ФД № 27001RMFS5, исходя из сложной и простой процентной ставки (данные взяты из задачи 3):
Простая ставка:
Сложная ставка:
Определим доходность всего портфеля исходя из рассчитанных доходностей отдельных облигаций. Для этих целей составим табл. 6.5.
Таким образом, доходность портфеля государственных облигаций рассчитанная на основе простой процентной ставки равна 26,27%, а на основе сложной процентной ставки — 28,93%.
Задача №51.
Допустим, коммерческий банк должен осуществить через два года платеж на 1 ООО ООО руб. На рынке имеется два вида облигаций:
• типа А — одногодичная дисконтная облигация номиналом 1000 руб. (ГКО);
• типа В — трехгодичная купонная облигация с купонной ставкой 8% и номинальной стоимостью 1000 руб. (ОФЗ-ПД).
Требуется построить портфель, полностью хеджирующий риск изменения процентной ставки при условии, что текущая процентная ставка равна 10%, и рассчитать, как изменится полная стоимость портфеля для различных процентных ставок — 9, 10 и 11%.
Решение:
Рассчитаем дюрацию трех летней облигации (табл. 6.7).
Рассчитаем число облигаций типа 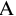
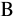
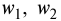
Для нахождения весов надо решить систему уравнений:
Если будущая стоимость портфеля должна быть равна 1000 000 руб., то облигаций обоих типов, с учетом текущей процентной ставки (10%), следует взять на сумму равную 1000 000/1,21 = = 826 446,28 руб.
Облигаций типа 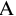
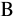
Представим в табл. 6.8 структуру портфеля, хеджирующего риск изменения процентных ставок (в штуках облигаций).
Расчет портфеля облигаций для различных процентных ставок показан в табл. 6.9.
Итак, портфель иммунизирован к риску изменения процентной ставки, но остаются риск ликвидности и риск неуплаты. В реальности сдвиг кривой доходности к погашению не всегда параллелен и обеспечить согласованность денежных потоков не всегда просто. Для этого нужно использовать более сложные формы кривых до-ходностей.
Задача №55.
Стартовая стоимость объекта лизинга 3,6 млн руб.; период полной амортизации около 12 месяцев, равномерно по месяцам; учетная ставка ЦБ РФ 11% годовых. В связи с размером вышеуказанной ставки, амортизационных отчислений, а также комиссионных лизингодателя (например, в размере 6% годовых) и других расходов ежемесячные отчисления в покрытие издержек по оказанию кредитных и других услуг составят 1,4% в месяц от фактически задействованных финансовых средств.
Составьте график лизинговых платежей и определите общую сумму расходов лизингополучателя. Выявите преимущество получения оборудования по лизингу по сравнению с приобретением его за счет кредита под проценты на уровне учетной ставки Центрального банка РФ.
В целях наглядной иллюстрации отдельных преимуществ финансовой модели лизинга по сравнению с традиционной схемой приобретения оборудования за счет кредита в данном примере используется упрощенная схема расчета лизинговых платежей по формуле
где 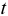
Решение:
График лизинговых платежей представлен в табл. 7.3.
Таким образом, за весь период действия лизингового соглашения, предусматривающего полную финансовую амортизацию объекта лизинга в течение одного года, расходы лизингополучателя, распределенные на 12 месяцев, составят 4320,2 тыс. руб. (без НДС), причем на долю кредитных и других услуг придется 360,2 тыс. руб., что составляет 9,1% стоимости объекта (для сравнения — учетная ставка ЦБ РФ равна 11%), т.е. ниже ставки рефинансирования на 1,9 пунктов. Следовательно, приобретение оборудования по лизингу более выгодно, нежели за счет кредита.
Лизинг имеет преимущества перед кредитом, поскольку предполагает 100%-ное кредитование, в то время как получить кредит можно только на определенную сумму оборудования (в пределах 75%). Мелким и средним компаниям проще получить лизинг, нежели кредит из-за необходимости дополнительной гарантии по кредиту.
Лизинговое соглашение более гибко, чем кредит, поскольку предоставляет возможность выработать удобную для покупателей схему финансирования, заключающуюся в сроках оплаты арендной платы, начало которой можно отсрочить на определенный период времени, что невозможно при кредитовании, суммы платежей и снижении налогооблагаемой прибыли у арендатора, так как лизинговые платежи включаются в себестоимость товара, в то время как выплаты кредита осуществляются за счет прибыли.
Однако нельзя считать, что у лизинга нет недостатков — арендатор не выигрывает на повышении остаточной стоимости оборудования, лизинг дороже кредита, при финансовом лизинге даже за устаревшее оборудование приходится платить до окончания срока договора. В то же время риск устаревания оборудования, прежде всего морального, целиком ложится на арендодателя.
Задача №63.
15 ноября 2005 г. клиент открыл в банке счет на один год и один месяц под 9% годовых (процентная ставка фиксированная, т.е. неизменна в течение всего срока хранения). Проценты согласно условиям договора начисляются по истечении каждого трехмесячного периода, определяемого с даты открытия счета по вкладу (с даты пролонгации) и по истечении основного (пролонгированного) срока хранения вклада.
В случае досрочного востребования суммы вклада в течение основного (пролонгированного) срока хранения вклада доход за неполный срок хранении исчисляется: при досрочном востребовании в течение первых 2000 дней — исходя из процентной ставки 0,1% годовых, по истечении 200 дней — исходя из 1/2 процентной ставки по вкладу.
Первоначальный взнос составил 12 140 руб. 00 коп. 14 апреля 2006 г. клиент внес дополнительный взнос 5000 руб. Счет был закрыт 19 декабря 2006 г.
Требуется определить сумму, полученную клиентом банка при закрытии счета.
Решение:
Дата окончания срока хранения вклада 15 декабря 2006 г., дата возврата вклада по договору 16 декабря 2006 г.
Произведем расчеты.
15 ноября 2005 г. открытие счета — 12 140 руб. 00 коп.
15 февраля 2006 г. осуществлена капитализация процентов:
14 апреля 2006 г. произведен дополнительный взнос: 5000 руб. 00 коп.
15 мая 2006 г. осуществлена капитализация процентов:
15 августа 2006 г. осуществлена капитализация процентов:
15 ноября 2006 г. осуществлена капитализация процентов:
15 декабря 2006 г. причислены проценты:
19 декабря 2006 г. произведено закрытие счета:
Сумма, полученная клиентом банка при закрытии счета, составит 18 676 руб. 77 коп.
Задача №64.
Пенсионный пополняемый депозит открыт 4 января 2006 г. на сумму 1000 руб. Дата окончания срока хранения 5 апреля. Процентная ставка по вкладу 7,5% годовых. 10 февраля 2006 г. сделан дополнительный взнос в сумме 500 руб. Требуется рассчитать сумму дохода, которую получит вкладчик по окончании срока вклада.
Решение:
Вначале определим, что 1 марта вкладчик получает проценты за первый полный месяц хранения, который истек 4 февраля. 9 марта вкладчик получает проценты за второй полный месяц хранения, который истек 4 марта. Расчет дохода будет следующий.
Сумма процентов, подлежащих выплате вкладчику 1 марта, составит на сумму первоначального взноса: 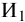
На сумму дополнительного взноса проценты не начисляются, так как дополнительный взнос не находится на хранении в месяце, за который исчисляется доход.
Сумма процентов, подлежащих выплате 9 марта составит на сумму первоначального взноса: 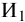
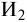
Общая сумма процентов, подлежащих выплате, составит 8,01 руб. (5,75 2,26). Сумма процентов, подлежащих причислению к остатку вклада по истечении срока 5 апреля 2006 г., будет равна:
1) на сумму первоначального взноса: 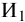
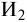
Итого получим 9,87 руб. (6,58 3,29). Данная сумма присоединяется к сумме вклада и выводится новый остаток по состоянию на начало следующего срока хранения: 1500 9,87 = 1509,87 руб.
Задача №65.
Дата окончания предыдущего срока хранения 5 апреля. Остаток вклада после пролонгации составил 1509,87 руб., из них 9,87 руб. — причисленные к остатку вклада проценты за истекший срок хранения. Дата окончания нового срока 6 июля. Процентная ставка по вкладу 7,5% годовых.
Решение:
Сумма процентов, подлежащих выплате вкладчику 6 июля составит на сумму вклада, числящего на начало срока: 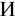
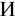
Последняя сумма (0,34 руб.) присоединяется к сумме вклада и выводится новый остаток по состоянию на начало следующего срока хранения: 1509,87 0,34 = 1510,21.
В случае востребования вкладчиком всей суммы вклада до истечения первого пролонгированного им срока хранения доход на все суммы исчисляется по ставке вклада до востребования.
Задача №67.
Вклад «Депозит Сбербанка России» (8000 руб.) был открыт 2 февраля на три месяца и один день со ставкой процентов, равной 5,25% годовых. Вкладчик пришел получить сумму вклада 8000 руб. с причитающимися процентами 9 июня (количество дней в месяце в формуле процентов по вкладу «срочный депозит» принимается за 30 дней). Требуется определить сумму причисленных процентов.
Решение.
Исчислим проценты за установленный срок:
где 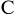
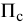
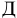
Проценты до востребования исчисляются по формуле
где 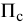
Со 2 февраля по 3 мая проценты начисляются по формуле и по ставке «Депозита Сбербанка России» (за 90 дней):
Первый вариант. С 3 мая по 9 июня (сами эти даты не включаются в количество дней) проценты рассчитываются по ставке до востребования (29 дней в мае 8 дней в июне = 37 дней), т.е.:
Второй вариант. Если вкладчик явился 15 марта, надо рассчитать причитающуюся ему сумму. Так как срочность вклада нарушена, проценты начисляются по ставке до востребования со 2 февраля по 15 марта (не включая эти даты):
Задача №682 (расчет величины чистых денежных средств)
Организация занимается производством продукции. Остаток денежных средств по состоянию на 01.01.2022 составил 400 тыс. руб. По итогам 2022 г. организация получила от покупателей денежные средства в размере 3200 тыс. руб. Сумма денежных средств, направленных на оплату сырья, – 1000 тыс. руб., услуг сторонних организаций – 300 тыс. руб.
Определите величину чистых денежных средств от текущей деятельности и чистое увеличение денежных средств и их эквивалентов.
Решение задачи:
Величина чистых денежных средств от текущей деятельности составляет:
3200 – 1000 – 300 – 70 – 50 =1780 тыс. руб.
Чистые денежные средства от инвестиционной деятельности составили -700 тыс. руб.
Финансовую деятельность организация не осуществляла, следовательно, отсутствует показатель чистых денежных средств от финансовой деятельности.
Чистое увеличение денежных средств и их эквивалентов составляет сумму показателей чистых денежных средств от текущей, инвестиционной и финансовой деятельности. Таким образом, чистое увеличение денежных средств и их эквивалентов составит:
1780 – 700 = 1080 тыс. руб.
Задача №70.
В банк за кредитом на неотложные нужды обратился заемщик, среднемесячный доход (чистый доход) которого за шесть месяцев составляет 2000 руб. Срок кредитования пять лет. Процентная ставка по кредиту 17% годовых. Требуется определить платежеспособность заемщика и максимальный размер кредита. Составить график платежей по кредиту.
Решение:
Для решения этой задачи следует знать, что при выдаче кредита оценка платежеспособности заемщика не производится. Залоговая стоимость ценных бумаг должна быть не менее суммы обязательств заемщика на момент возврата задолженности с учетом причитающихся за пользование кредитом процентов.
Максимальный размер кредита рассчитывается исходя из залоговой стоимости ценных бумаг:
где 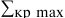
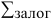
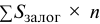
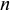
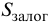
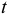
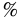
При принятии в залог разных видов ценных бумаг залоговая стоимость портфеля рассчитывается как сумма залоговых стоимостей каждого вида ценных бумаг. При принятии в залог акций Сбербанка России залоговая стоимость одной акции признается равной рыночной цене за вычетом величины установленного дисконта (величина дисконта устанавливается Кредитным комитетом Сбербанка России).
где 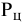
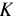
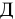
Используя указанные формулы, определим оценочную стоимость акций:
Определим размер кредита (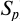
Методы денежно-кредитной политики центрального банка
В условиях развития современной банковской системы особая роль в ней принадлежит центральному банку как представителю первого яруса банковской системы. Центральный банк в настоящее время имеется в каждой стране. Его возникновение было связано в первую очередь с монополизацией денежного обращения.
Впоследствии на него были возложены и другие важные функции, например: «банк банков», когда он является кредитором последней инстанции для них, осуществляет расчеты; банк правительства; хранитель золотовалютных резервов, которые выступают в качестве балансирующей статьи платежного баланса.
Центральный банк осуществляет и такую функцию, как банковский надзор и контроль. Но со второй половины XX в. основной его функцией становится денежно-кредитное регулирование экономики, основы которого были заложены Кейнсом в 1936 г. в книге «Общая теория занятости, процента и денег».
В условиях Великой депрессии возникла необходимость вывода экономики из этого состояния, и Кейнс разработал теорию дефицитного финансирования экономики, что могло помочь увеличить темпы роста экономики, стимулировать ее развитие. Он предложил такую схему денежно-кредитного регулирования: изменение денежной масы приводит к изменению процента, что сказывается на инвестициях и отражается в изменении ВНП.
На разных этапах промышленного цикла центральный банк, благодаря своему положению имеет возможность либо увеличивать денежную массу в экономике (проводить кредитную экспансию), а это впоследствии вызывает увеличение ВНП, либо уменьшать денежную массу (кредитная рестрикция), что приводит к удорожанию денег и снижению инвестиций, а как следствие — к уменьшению ВНП.
Основными методами увеличения или уменьшения денежной массы становится не элементарное «печатание денег» или фискальное их изъятие, а воздействие на имеющуюся в стране денежную массу посредством регулирования денежных потоков у коммерческих банков. На денежном рынке в качестве основных «продавцов» денежных средств выступают коммерческие банки, покупателей — корпорации, население, государство.
Основными методами денежно-кредитной политики центрального банка являются:
- политика обязательного резервирования;
- политика открытого рынка;
- учетная политика.
Рынок ценных бумаг
Рынок ценных бумаг — часть финансового рынка государства. Как свидетельствует мировой опыт, рынок ценных бумаг играет большую роль в развитии экономики: государственные ценные бумаги дают возможность финансировать государственные расходы, поддерживать ликвидность банковской системы.
Наличие разных форм собственности, акционерных обществ и возможность привлекать необходимые средства путем выпуска ценных бумаг обусловили создание механизма перераспределения денежных накоплений через рынок ценных бумаг, способствующий мобилизации денежных ресурсов на макро- и микроуровнях.
Эмиссия ценных бумаг является важнейшей функцией процесса привлечения капитала. Именно через нее осуществляется объединение денежных средств для покрытия текущего и накопленного дефицитов государственного и муниципальных бюджетов.
Ценные бумаги и фондовые рынки представляют собой важный источник финансирования деятельности всех видов предприятий.
Первичное размещение ценных бумаг эмитирующей корпорацией (АО) или правительственным органом частному либо государственному инвестору называется первичным рынком ценных бумаг. Любая торговля ценными бумагами после их первичного предложения означает их вторичное размещение и относится ко вторичному рынку ценных бумаг.
Вложение средств в акции дает возможность получить долгосрочный прирост капитала, дивиденды и защиту от инфляции. Однако даже обладание самыми лучшими акциями не дает гарантий высокой доходности или вообще получения какого-либо дохода. Более привлекательными для инвесторов являются государственные ценные бумаги как более надежные.
В связи с этим формирование портфеля ценных бумаг инвесторами требует изучения самих этих бумаг, их различий, доходности, обращения на вторичном рынке. Кроме того, необходимо владеть методами анализа факторов, влияющих на развитие рынка ценных бумаг, его объемы, надежность состояния и доходность, формирование портфеля ценных бумаг.