Гарантированный рост

Где ar – требуемый уровень приростной капиталоемкости.
3) Естественный рост:
Где n – темп роста предложения труда;
g – темп роста производительности труда.Производственная функция Кобба-Дугласа:
Где Y – объем производства;
K – затраты капитала;
L – затраты труда;
А, б и в – параметры, или коэффициенты производственной функции: А – коэффициент пропорциональности; б и в – коэффициенты эластичности объема производства по затратам труда и капитала.
Модель роста Р. Солоу:
Где ш – капиталовооруженность труда;
qt – средняя производительность труда, или доход на одного занятого;
n – темп роста населения;
Sy – норма сбережений.«Золотое правило» накопления:
Где 
r – ставка процента.Примеры решения задач
- Экономика страны описывается производственной функцией вида Y = A·K0,4·L0,6. Известно, что темп прироста капитала равен 3% в год, а численности занятых – 2%. Общая производительность факторов растет с темпом 1,5% в год. Как меняется объем производства?
Решение
В неоклассической модели роста была использована производственная функция вида Y = AF(K,L). Объем производства Y зависит от вклада факторов – труда L и капитала K, а также от технологии. Производственная функция имеет постоянную отдачу от масштаба, т. е. увеличение всех факторов в определенной степени приводит к росту выпуска в той же степени.
Разделим это выражение на Y = AF(K,L) и получим: 
Второе и третье слагаемое в правой части уравнения умножим и разделим на К и L
В скобках мы получим доли капитала и труда в общем объеме выпуска. При условии постоянной отдачи от масштаба сумма этих долей равна единице (по теореме Эйлера), тогда
где б – доля капитала, а (1 – б) – доля труда в доходе, А – общая производительность факторов, мера уровня технологического прогресса, измеряемая обычно по остаточному принципу («остаток Солоу»).
В представленной функции Y = A·K0,4·L0,6 показатели степени представляют и долю факторов в доходе, то есть

что можно проверить математически, проведя с этой функцией все указанные выше операции.Тогда 
- Производственная функция задана уравнением

Норма сбережения s равна 0,2, норма выбытия d – 5%, тем роста населения n составляет 2% в год, темп трудосберегающего технологического прогресса g равен 3%. Каким будет запас капитала и объем выпуска в расчете на одного занятого в устойчивом состоянии? Соответствует ли устойчивая фондовооруженность уровню, при котором достигается максимальный объем потребления («золотому правилу»)? Какой должна быть норма сбережения в соответствии с «золотым правилом»?
Решение
Преобразуем производственную функцию, разделив ее на L, то есть представим все параметры в расчете на одного занятого, тогда:
где 


















Государство в системе макроэкономического регулирования
Располагаемый доход при наличии подоходного налогообложения:
Yd=Y–T
Где Yd – располагаемый доход;
Y – совокупный доход;
Т- сумма налогов.Налоговая функция:
T = Ta t*Y
Где Та – объем автономных (т.е. не зависящих от совокупного дохода) налоговых поступлений;
t – ставка налога (налоговая ставка);
У – совокупный доход.Потребительская функция с учетом налогов:
С = Са МРС*(Y-Т).Мультипликатор налогов

Сложный мультипликатор расходов:
Мультипликатор налогов при наличии встроенных стабилизаторов:
Мультипликатор сбалансированного бюджета:
Где ДВ – изменение бюджета.Эффект торможения динамики производства с учетом встроенных стабилизаторов:
Где Да- изменение компонента совокупных расходов.
Процесс мультипликативного расширения денежной массы (предложения денег):
Где Ms – денежная масса (предложение денег);
MB – денежная база;
rr – норма обязательного минимального резервирования вкладов (норма резервирования);

Примеры решения задач
Задача 1. В смешанной равновесной экономике закрытого типа имеем условия: частные сбережения = 1000 ден. ед., инвестиции = 900 ден. ед. Чему равны государственные сбережения?
Решение
В равновесной экономике инвестиции равны сбережениям:
I = S.
Однако, по условию нашей задачи, экономика является смешанной. Поэтому валовые сбережения следует разделить на две категории: личные (частные) сбережения (SP), куда входят собственно личные сбережения и сбережения предприятий, и избыток государственного бюджета (SG), равный излишку налоговых поступлений государства над его совокупными расходами. Тогда тождество сбережений и инвестиций примет вид:
I = SP SG.Отсюда, государственные сбережения:SG = I – SP.SG = 900 – 1000 = 100 ден. ед.
Задача 2. В смешанной экономике закрытого типа имеем условия: Y = 1000 грн., I = 120 грн., С = 700 грн. государственные сбережения = – 20 грн. Чему равны чистые налоги?
Решение
Для закрытой экономики смешанного типа основное макроэкономическое тождество имеет вид:Y=C G IГде С – потребительские расходы;
I – инвестиционные расходы;
G – государственные расходы.
Государственные сбережения определяются как:Sg = T-GГде Т – налоги.
Отсюда: Т = Sg G.
Величину государственных расходов определим из основного макроэкономического тождества:
G = Y – С – I = 1000-700- 120 = 180 грн.
Тогда величина чистых налогов составит:
Т= -20 180 =160 грн.
Задача 3. MPC=0,75, предельная налоговая ставка t = 0,2. В соответствии с прогнозом в условиях неполной занятости частные инвестиции возрастут на 50 млн. ден. ед., Р = 1,0. Чему равен эффект торможения реального ВВП, вызванный чистыми налогами?
Решение
Эффект торможения реального ВВП, вызванный увеличением чистых налогов и инвестиций рассчитаем при помощи следующей формулы:
Где 

Задача 4. Норма обязательных резервов составляет 0,1. Государственный бюджет сведен с дефицитом в 300 млрд. грн. Правительство решило покрыть дефицит на 1/3 за счет денежной эмиссии, а на 2/3 за счет выпуска облигаций. Как может измениться предложение денег, если НБУ выкупит 1/4 часть выпущенных облигаций.
Решение
Поскольку дефицит госбюджета покрывается частично за счет выпуска облигаций (300*2/3 = 200 млрд. грн.), то 1/4 часть выкупленных НБУ облигаций составит 200*1/4 = 50млрд. грн. Когда НБУ покупает облигации, он увеличивает сумму на резервных счетах коммерческих банков, у которых он покупает облигации, соответственно в банковскую систему поступают дополнительные «деньги повышенной мощности» и начинается процесс мультипликативного расширения денежной массы (предложения денег):
Механизм внешнеэкономической деятельности
Основные уравнения платежного баланса: в открытой экономикеСледовательно:
Где NX – чистый экспорт;
Y – совокупный выпуск внутри страны;
C I G – сумма расходов отечественных экономических субъектов на покупку товаров, произведенных внутри страны.
Далее, поскольку объем совокупного выпуска равен объему совокупного дохода, который расходуется на уплату налогов, частное потребление и частные сбережения:
Сальдо баланса по счетам капиталовложений = – Сальдо баланса по текущим операциям;
Сальдо баланса по счетам капиталовложений Сальдо баланса по текущим операциям =0.
Валютный курс:
Реальный валютный курс = Номинальный валютный курс 
Реальный прямой валютный курс = 

Условия торговли:Где 
Pex – экспортные цены;
Pim – импортные цены.Функция спроса на импорт:

Где 


Функция чистого экспорта:
Где NX – величина чистого экспорта;
Ex – объем экспорта из данной страны;
X0 – сальдо экспорта и автономного импорта.
Мультипликатор государственных закупок с учетом внешней торговли:

Где МРС – предельная склонность к сбережению;МРX – предельная склонность к импортированию.
Налоговый мультипликатор с учетом внешней торговли:
Примеры решения задач
Задача 1. Допустим, что Германия импортирует продукт А из США. Цена этого продукта составляет 5 долларов за 1 кг. Сколько он будет стоить в Германии при валютном курсе 1 евро = 0,64 доллара?
Решение
Сначала необходимо выразить стоимость доллара через евро. Поскольку 1 евро = 0,64 доллара, то составим следующую пропорцию:
1 евро = 0,64 доллара
х евро = 1 доллар.
Отсюда, 1 доллар = 1,5625 немецкой марки.
Таким образом, стоимость продукта А в Германии составит:
5 х 1,5625 = 7,8125 евро.
Задача 2. Функция спроса на товар Х в стране А имеет вид: DA = 80 – 20 Р, функция предложения SA = – 70 40Р. Функции спроса и предложения на этот товар в стране В, соответственно, DB = 90 – 10Р и SB = 30 20Р. Определить уровень мировой цены (Р), объем продаж при установлении торговых отношений между странами.
Решение
При торговле между двумя странами с большой открытой экономикой мировая цена устанавливается на таком уровне, чтобы общий объем спроса на данный товар обеих стран был полностью удовлетворен суммарным объемом предложения этого товара обеими странами, т.е. чтобы:DA DB = SA SB.Таким образом, мировую цену определим из уравнения:
(80 – 20Р) (90 – 10Р) = (-70 40Р) (30 20Р)
Рm = 2,333(3).
Теперь необходимо установить, какая страна будет экспортировать, а какая импортировать товар Х для чего необходимо рассчитать внутреннюю цену на товар Х в стране А и в стране В на основе равенства спроса и предложения:
Для страны А: DA = SA, 80 – 20 Р = – 70 40Р, следовательно, РА = 2,5.
Для страны В: DB = SB, 90-10Р = 30 20Р, следовательно, РВ = 2.
Можно сделать вывод, что страна В будет экспортировать товар Х, поскольку ее внутренняя равновесная цена ниже мировой, а страна А будет импортировать товар Х, т.к. ее внутренняя равновесная цена превышает мировую. Тогда объем экспорта из страны В и импорта в страну В составит:
SB – DB = DA-SA = 30 20Р – 90 10Р = 80 – 20Р 70 – 40 Р = 150 – 60 Р = 150 – 60х2,333 = 10 ед. товара Х.
Задача 3. Чему равен мультипликатор государственных расходов в открытой экономике, если предельная склонность к потреблению (МРС) = 0,9, предельная ставка налога (t) = 0,25, предельная склонность к импортированию = 0,2?
Решение
Мультипликатор государственных расходов в открытой экономике рассчитывается по формуле:

Мультипликатор с учетом предельной налоговой ставки примет вид:
Где МРС – предельная склонность к сбережению;
t – предельная налоговая ставка;
MPX – предельная склонность к импортированию.
Задача 4. Используя модель мультипликатора, определить прирост равновесного ВНП в результате получения экспортного заказа на 6 млн. грн при условии, что на потребление расходуется 80% прибыли, приобретение импортных товаров составляет 40% расходов.
Решение
При наличии внешней торговли
Где Y – объем произведенной продукции (ВНП);
G – государственные закупки;
I – инвестиции;
NX – чистый экспорт.
Прирост ВНП в модели открытой экономики с использованием мультипликатора определяем по формуле:

МРС – предельная склонность к потреблению;
МРХ – предельная склонность к импорту.
По условию нашей задачи, МРС = 80% или 0,8 в абсолютном выражении, а МРХ = 40% = 0,4. Таким образом, мы сможем определить прирост ВНП:
Задача: решение задач по макроэкономике –
Изменения масштаба производства в λ раз выражается переходом к объему затрат λх. Объем выпуска продукции тогда может быть описан с помощью Y=f(λх), где х=(х1, х2, …, хn), где Хi – i-й фактор производства. Вопрос об изменении эффективности в зависимости от масштабов производства легко можно решить в том случае, если производственная функция обладает свойством однородности.
Однородная производственная функция – функция, обладающая свойством:
Y=f(λх1, λх2, …, λхn)=λkf(λх1, λх2, …, λхn),
где k – степень однородности.
Однородность производственной функции означает, что пропорциональный рост всех факторов производства в λ раз ведет к увеличению роста объема производства в λk раз. При λ=1 эффективность в связи с увеличением масштабов производства не изменяется, при k>1 эффективность возрастает, при k<1 она снижается.
Проведя соответствующие преобразования выражений, данных в условиях задачи, производственных функций, получим соответствующее значение коэффициента k: k<1, k=1, k>1.
Приведем решение для каждого из предложенных вариантов задачи:
Y=(4К2 3L2)0,5 – однородная функция. Увеличение масштабов производства в λ раз для производства, описываемого функцией, соответствует замене последней функцией Y=(4(λК)2 3(λL)2)0,5=(4λ2К2 3λ2L2)0,5=λ2×0,5×(4К2 3L2)0,5 или λ×(4К2 3L2)0,5, т.е. в данном случае k=1;
Увеличение масштаба производства в λ раз для третьей функции соответствует замене производственной функции Y=2K0,4×L0,6 функцией Y=2(λK)0,4×(λL)0,6. Проведем некоторые преобразования: Y=2(λK)0,4×(λL)0,6=2λ0,4K0,4λ0,4L0,6=2λK0,4L0,6=λ×(2K0,4L0,6). Получим k=1.
В последнем варианте Y=1/3×(K×L2)0,5 – функция неоднородная. Проведем ее преобразование в соответствии с увеличением масштаба производства в λ раз. Это соответствует замене искомой функции производственной функцией Y=1/3×(λK×(λL)2)0,5=1/3×λ3×0,5×(KL)2)0,5=1/3×λ1,5×(KL)2)0,5, k>1.
Примеры решения задачи по финансовой математике в excel и видеоурок
Ниже приведены условия задач и текстовый отчет о решении. Закачка полного решения(файлы doc и xls в архиве zip) начнется автоматически через 10 секунд.
Задача 1
Постановка задачи.
Пусть инвестиции в проект к концу первого года его реализации составят 20 000 руб. В последующие четыре года ожидаются годовые доходы по проекту: 6 000 руб., 8 200 руб., 12 600 руб., 18 800 руб.
Рассчитать чистую текущую стоимость проекта к началу первого года, если процентная ставка составляет 10% годовых.
Алгоритм решения задачи.
Чистая текущая стоимость проекта для периодических денежных потоков переменной величины рассчитывается с помощью функции ЧПС.
Так как по условию задачи инвестиция в сумме 20 000 руб. вносится к концу первого периода, то это значение следует включить в список аргументов функции ЧПСсо знаком «минус» (инвестиционный денежный поток движется «от нас»). Остальные денежные потоки представляют собой доходы, поэтому при вычислениях укажем их со знаком «плюс».
Иллюстрация решения задачи представлена на рис. 4.7.
Чистая текущая стоимость проекта к началу первого года составляет:
= ЧПС (10%; -20000; 6000; 8200; 12600; 18800) = 13 216,93 руб.
Данный результат представляет собой чистую прибыль от вложения 20 тыс. руб. в проект с учетом покрытия всех расходов.
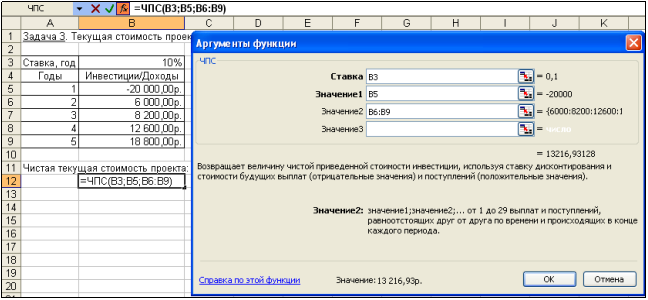
Рис. 4.7. Фрагмент окна Excel с панелью функции ЧПС
При расчете чистой приведенной стоимости инвестиций с помощью функции ЧПС учитываются периодические платежи переменной величины как суммы ожидаемых расходов и доходов в каждый из периодов, дисконтированные нормой процентной ставки, с использованием следующей формулы:
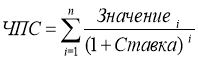 (4.8),
(4.8),
где: ЧПС – чистая текущая стоимость периодических выплат и поступлений;
Значениеi – суммарный размер i-го денежного потока на конец периода (поступления – со знаком «плюс», выплаты – со знаком «минус»);
Ставка– норма дисконтирования за один период;
n – число периодов движения денежных потоков (суммарное количество выплат и поступлений);
i– номер периода денежного потока.
Аналитический расчет задачи дает аналогичный результат:
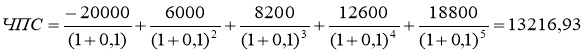
Задача 2
Постановка задачи.
Инвестор с целью инвестирования рассматривает 2 проекта, рассчитанных на 5 лет. Проекты характеризуются следующими данными:
- по 1-му проекту – начальные инвестиции составляют 550 тыс. руб., ожидаемые доходы за 5 лет соответственно 100, 190, 270, 300 и 350 тыс. руб.;
- по 2-му проекту – начальные инвестиции составляют 650 тыс. руб., ожидаемые доходы за 5 лет соответственно 150, 230, 470, 180 и 320 тыс. руб.
Определить, какой проект является наиболее привлекательным для инвестора при ставке банковского процента – 15% годовых.
Алгоритм решения задачи.
Оценку привлекательности проектов выполним с помощью показателя чистой текущей стоимости (функции ЧПС).
Поскольку оба проекта предусматривают начальные инвестиции, вычтем их из результата, полученного с помощью функции ЧПС. (Начальные инвестиции по проекту не нужно дисконтировать, так как они являются предварительными, уже совершенными к настоящему моменту времени).
Для облегчения анализа полученного решения исходные данные задачи представим в виде таблицы и в соответствующие ячейки введем значения формул с функциями ЧПС (рис. 4.8).В результате вычислений получим, что чистая приведенная стоимость инвестиций во второй проект почти на 22 тыс. руб. выше, чем в первый.


Непосредственное задание параметров в формулах расчета, как и вычисления с использованием формулы (4.8), дают те же результаты.
Для первого проекта:
= ЧПС (15%; 100000; 190000; 270000; 300000; 350000) – 550000 = 203 691,03р.
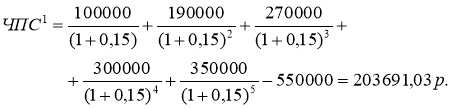
Для второго проекта:
= ЧПС (15%; 150000; 230000; 470000; 180000; 320000) – 650000 = 225 392,59р.
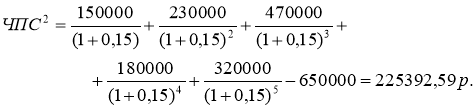
Таким образом, второй проект является для инвестора более привлекательным.
В некоторой степени функции ПС и ЧПСпохожи. Сравнивая их, можно сделать следующие выводы:
1) в функции ПС периодические выплаты предполагаются одинаковыми, а в функции ЧПС они могут быть различными;
2) в функции ПС платежи и поступления происходят как в конце, так и в начале периода, а в функции ЧПС предполагается, что все выплаты производятся равномерно и всегда в конце периода.
Из последнего вывода следует, что если денежный взнос осуществляется в начале первого периода, то его значение следует исключить из аргументов функции ЧПС и добавить (вычесть, если это затраты) к результату функции ЧПС. Если же взнос приходится на конец первого периода, то его следует задать в виде отрицательного первого аргумента массива значений функции ЧПС.
Примечание.
Нельзя непосредственно оценивать эффективность, например, с помощью функции ЧПС, нескольких инвестиционных проектов, имеющих разную продолжительность. Предполагая, что допускается реинвестирование, необходимо свести полученные результаты чистой текущей стоимости по каждому из них к единому по продолжительности периоду. С этой целью можно воспользоваться специальными методами.
Метод цепного повтора предполагает оценку эффективности проектов в рамках общего одинакового срока их действия. Находится наименьшее общее кратное продолжительности проектов и рассчитывается, сколько раз каждый из них должен повториться. Затем определяется с учетом повторов и реинвестирования чистая приведенная стоимость каждого из проектов, которая и сравнивается. Большему значению соответствует более привлекательный проект.
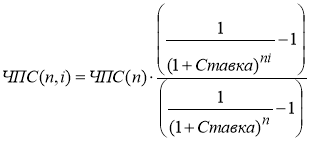
Суммарная чистая приведенная стоимость повторяющегося потока для каждого из проектов находится по формуле:
 (4.9),
(4.9),
где: ЧПС(n) – чистая приведенная эффективность исходного проекта, найденная с учетом предварительных инвестиций;
n– длительность исходного проекта;
i – число повторов исходного проекта;
Ставка – норма дисконтирования за один период.
Метод бесконечного цепного повтора предполагает, что каждый из проектов может быть реализован неограниченное число раз.
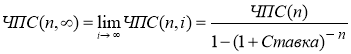 (4.10)
(4.10)
Задача 3
Постановка задачи.
Сравнить инвестиционную привлекательность двух проектов. Цена капитала составляет 10%. Предварительные инвестиции в первый проект составляют 100 млн. руб., во второй – 105 млн. руб. Продолжительность первого проекта – 2 года; доходы по годам – 50 и 70 млн. руб. соответственно. Продолжительность второго проекта – 3 года; доходы по годам – 34, 40 и 60 млн. руб. соответственно.
Алгоритм решения задачи.
Для решения задачи предварительно рассчитаем чистую приведенную стоимость проектов при их однократном выполнении, воспользовавшись функцией ЧПС и вычтя предварительные инвестиции. Затем, принимая во внимание разную продолжительность проектов, рассчитаем значения эффективности проектов по формулам (4.9) и (4.10).
При однократном выполнении проектов предпочтительным выходит второй проект (ЧПС1= 3,306; ЧПС2 = 4,046). Но такой вывод преждевременный (рис. 4.9).
Расчет эффективности проектов за 6 лет, а также при их бесконечном повторении дает результат полностью противоположный – более привлекательным является первый проект:
ЧПС1(2,3) = 8,296 ЧПС2(3,2) = 7,086
ЧПС1(2,∞) = 19,048 ЧПС2(3, ∞) = 16,269






