Задача 9
Постановка задачи.
В целях покупки недвижимости инвестор взял в банке кредит в сумме 12 млн. руб. Определить ежемесячные выплаты по кредиту для разных процентных ставок и сроков погашения кредита.
Алгоритм решения задачи.
Ежемесячные выплаты по займу рассчитываются с использованием функции ПЛТ. Однако аргументы данной функции – процентная ставка и срок погашения кредита – по условию могут принимать различные значения. Поэтому рассмотрим влияние этих параметров на заданную функцию. Воспользуемся механизмом Таблица подстановки из меню команды Данные. Выполним следующую последовательность действий.
1. В ячейку электронного листа С3 введем числовое значение суммы кредита (12 000 000).
2. В ячейки С4, С5 введем произвольные (условные) значения процентной ставки (например, 5%) и срока погашения кредита в годах (например, 1), которые нам понадобятся при построении Таблицы подстановки.
3. В ячейки В9:В22 введем различные значения процентных ставок. В ячейки С9:К9 – возможные сроки погашения.
4. В ячейку В9 введем формулу для расчета ежемесячных выплат по займу: = ПЛТ (5%/12; 1*12; 12 000 000).
Заметим, что в качестве аргументов функции можно вводить как адреса ячеек, так и конкретные исходные значения.
5. Выделим интервал для таблицы данных, включающий формулу и все исходные данные, – В9:К22.
6. Выберем команды Данные → Таблица подстановки. В появившемся диалоговом окне (рис. 1.22) заполним соответствующие поля. Поскольку наша таблица зависит от двух параметров, то в поле «Подставлять значения по столбцам в:» введем ссылку на ячейку С5 (срок погашения), а в поле
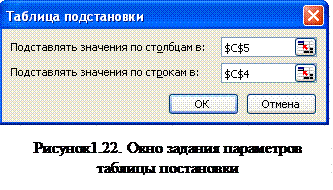
«Подставлять значения по строкам в» – ссылку на ячейку С4 (ставка).
7. Подтвердим ввод нажатием клавиши [Enter] или кнопкой ОК.
Таблица ежемесячных выплат по кредиту с помощью таблицы подстановки будет сформирована (рис. 1.23).
Задания для самостоятельной работы
1. Разработайте план погашения кредита, полученного на следующих условиях:
а) 700 тыс. руб. сроком на 6 лет под 9% годовых при выплате один раз в конце года.
б) 900 тыс. руб. сроком на 9 лет под 7% годовых при выплате один раз в квартал.
в) 500 тыс. руб. сроком на 4 лет под 11% годовых при выплате один раз в месяц.
2. Ипотечный кредит размером 2 200 000 руб. предоставлен по ставке 12% годовых сроком на 30 лет и требует ежемесячных платежей. Каков будет остаток основной суммы через 8 лет?
3. Кредит в сумме 5 000 000 руб. предоставлен под 20% годовых сроком на 10 лет. Рассчитать величину остатка основной суммы без учета выплаченных процентов на начало третьего года.
4. Рассчитать сумму процентов, начисленных на вклад в 750 тыс. руб. за 2 года, если банк начисляет проценты ежеквартально из расчета 28% годовых. Какова должна быть годовая депозитная ставка при прочих равных условиях, если за 2 года необходимо удвоить первоначальный вклад?
5. Потребитель получает заем на покупку автомобиля 20 000$ под 8% годовых сроком на три года при ежемесячных выплатах. Какова будет сумма по процентам и основной платеж за первый и последний месяцы выплат?
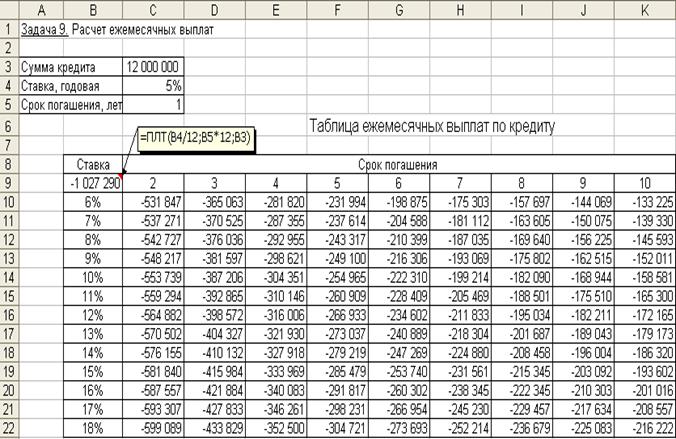
Рисунок 1.23. Фрагмент окна с таблицей ежемесячных выплат по кредит
Определить первоначальные затраты по проекту, если известно, что в последующие 4 года ожидаемые доходы будут соответственно: 300, 100, 400, 700 тыс. руб., при 9% норме дохода по проекту.
Определить внутреннюю скорость оборота инвестиции размером 55 тыс. руб., если в течение последующих 3 лет ожидаются годовые доходы соответственно: 9 тыс. руб., 17 тыс. руб., 23 тыс. руб.; на четвертый год ожидается убыток в размере 11 тыс. руб., а на пятый год – доход в размере 20 тыс. руб.
| Год | Денежный поток (тыс. руб.) |
Для реализации проекта потребовались первоначальные вложения за счет кредита в сумме 700 тыс. руб., взятого на 4 года по ставке 12% годовых. Ожидаемые доходы от проекта представлены в таблице.
· Рассчитать внутреннюю ставку доходности проекта.
· Рассчитать модифицированную ставку доходности проекта по истечении 4 лет, если все доходы реинвестировать в другой проект по ставке 15% годовых.
· Оценить экономическую эффективность проекта с учетом рыночной нормы дохода равной 11% (без реинвестирования доходов и с реинвестированием доходов).
Date: 2022-10-19; view: 4287; Нарушение авторских прав
§
Обзор ключевых категорий и положений
В Гражданском кодексе РФ (статья 142) ценная бумага определена как документ, удостоверяющий с соблюдением установленной формы и обязательных реквизитов имущественные права, осуществление или передача которых возможны только при его предъявлении.
Все ценные бумаги делятся на виды и типы.
Тип образует сочетание различных комбинаций видов ценных бумаг, объединяемых каким-либо общим признаком. Тип ценных бумаг подразделяется на их виды.
Вид – это качественная определенность какой-либо ценной бумаги, отличающая ее от других ценных бумаг. В рамках определенного вида ценной бумаги выделяются ее разновидности, которые в ряде случаев делятся еще дальше. Например, среди фондовых ценных бумаг, являющихся типом, можно выделить такие виды как акция или облигация. Разновидностью акций являются обыкновенные или привилегированные акции. Обыкновенная акция, в свою очередь, может быть одноголосной или многоголосной, с номиналом или без номинала и т.п.
Выделяют также срочные и бессрочные ценные бумаги. Последние представляют собой ценные бумаги, срок обращения которых ничем не регламентирован. Среди срочных ценных бумаг, т.е. имеющих установленный срок существования при их выпуске, выделяют краткосрочные (срок обращения до одного года); среднесрочные (срок обращения свыше одного года в пределах до 5-10 лет) и долгосрочные (срок обращения до 20-30 лет).
Основными видами ценных бумаг с точки зрения их экономической сущности являются: акции, облигации, депозитный и сберегательный сертификат, вексель, чек, коносамент, варрант, опцион, фьючерсный контракт.
Ценная бумага обладает определенным набором характеристик, среди которых можно выделить такие, как временные характеристики (срок существования и происхождение ценной бумаги), пространственные характеристики (форма существования, национальная и территориальная принадлежность), рыночные характеристики (тип использования, форма собственности и вид эмитента, форма выпуска, наличие дохода и другие).
Отметим основные экономические характеристики ценной бумаги.
Ликвидность, т.е. способность ценной бумаги к реализации, степень ее обратимости в денежные средства.
Доходность, предусматривающая отношение дохода, полученного от ценной бумаги (дивиденда, процента, премии), к инвестициям в нее.
Номинал – это стоимость ценной бумаги, которая указана на ней.
Курс – это цена, по которой ценные бумаги продаются и/или покупаются на фондовом рынке.
Надежность, предполагающая способность ценных бумаг выполнять возложенные на них функции в течение определенного промежутка времени в условиях равновесного рынка.
Каждый вид ценной бумаги характеризуется наличием в ней обязательных реквизитов – название ценной бумаги, серия, номер, наименование эмитента, наименование держателя ценной бумаги, ее номинальная стоимость и некоторые другие имущественно-обязательные условия.
Финансовые функции для работы с ценными бумагами
Для расчета и анализа различного типа ценных бумаг в Excel реализована специальная группа функций, расширенных специальным дополнением «Пакет анализа». Перечень таких функций представлен в таблице 1.4. В таблице 1.5 приведены описания аргументов функций.
Таблица 1.4– Назначение и форматы финансовых функций для анализа ценных бумаг
| Формат | Назначение |
| ДАТАКУПОНПОСЛЕ (дата_согл; дата_вступл_в_силу; частота; базис) | Возвращает число, представляющее дату следующего купона от даты соглашения. |
| ДАТАКУПОНДО (дата_согл; дата_вступл_в_силу; частота; базис) | Возвращает число, представляющее дату предыдущего купона до даты соглашения. |
| ДЛИТ (дата_согл; дата_вступл_в_силу; купон; доход; частота; базис) | Рассчитывает ежегодную продолжительность действия ценных бумаг, по которым осуществляются периодическая выплата процентов. |
| ДНЕЙКУПОН (дата_согл; дата_вступл_в_силу; частота; базис) | Возвращает число дней в периоде купона, который содержит дату расчета. |
| ДНЕЙКУПОНДО (дата_согл; дата_вступление_в_силу; частота; базис) | Возвращает количество дней от начала действия купона до даты соглашения. |
| ДНЕЙКУПОНПОСЛЕ (дата_согл; дата_вступл_в_силу; частота; базис) | Возвращает число дней от даты расчета до срока следующего купона. |
| ДОХОД (дата_согл; дата_вступл_в_силу; ставка; цена; погашение; частота; базис) | Возвращает доходность ценных бумаг (облигаций), по которым производятся периодические выплаты процентов. |
| ДОХОДКЧЕК (дата_согл; дата_вступл_в_силу; цена ) | Возвращает ставку годового дохода по ценным бумагам краткосрочного действия (доходность по казначейскому чеку или векселю). |
| ДОХОДПЕРВНЕРЕГ (дата_согл; дата_вступл_в_силу; дата_выпуска; первый_купон; ставка; цена; погашение; частота; базис) | Возвращает доход по ценным бумагам с нерегулярным (коротким или длинным) первым периодом. |
| ДОХОДПОГАШ (дата_согл; дата_вступл_в_силу; дата_выпуска; ставка; цена; базис) | Возвращает годовую доходность ценных бумаг, по которым проценты выплачиваются при наступлении срока погашения. |
| ДОХОДПОСЛНЕРЕГ (дата_согл; дата_вступл_в_силу; последняя_выплата; ставка; цена; погашение; частота; базис) | Возвращает доход по ценным бумагам с нерегулярным (коротким или длинным) последним периодом. |
| ДОХОДСКИДКА (дата_согл; дата_вступл_в_силу; цена; погашение; базис) | Возвращает годовую доходность по ценным бумагам, на которые сделана скидка. |
| ИНОРМА (дата_согл; дата_вступл_в_силу; инвестиция; погашение; базис) | Возвращает процентную ставку для полностью инвестированных ценных бумаг. |
| МДЛИТ(дата_согл; дата_вступл_в_силу; купон; доход; частота; базис) | Возвращает модифицированную продолжительность Макалея для ценных бумаг с предполагаемой номинальной стоимостью 100 руб., включая поправку, связанную с рыночным доходом и ежегодными выплатами по купонам. |
| НАКОПДОХОД (дата_выпуска; первый_доход; дата_согл; ставка; номинал; частота; базис) | Возвращает накопленный процент по ценным бумагам с периодической выплатой процентов. |
| НАКОПДОХОДПОГАШ (дата_выпуска; дата_согл; ставка; номинал; базис) | Возвращает накопленный процент по ценным бумагам, процент по которым выплачивается в срок погашения. |
| ПОЛУЧЕНО (дата_согл; дата_вступл_в_силу; инвестиция; скидка; базис) | Возвращает наращенную сумму, полученную к сроку погашения полностью обеспеченных ценных бумаг. |
| РАВНОКЧЕК (дата_согл; дата_вступл_в_силу; скидка) | Возвращает эквивалентный облигации доход по казначейскому векселю. |
| СКИДКА (дата_согл; дата_вступл_в_силу; цена; погашение; базис) | Возвращает ставку дисконтирования для ценных бумаг. |
| ЦЕНА (дата_согл; дата_вступл_в_силу; ставка; доход; погашение; частота; базис) | Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, по которым выплачивается периодический процент. |
| ЦЕНАКЧЕК (дата_согл; дата_вступл_в_силу; скидка) | Возвращает цену на 100 руб. номинальной стоимости для бумаг краткосрочного действия (казначейского чека или векселя). |
| ЦЕНАПЕРВНЕРЕГ (дата_согл; дата_вступл_в_силу; дата_выпуска; первый_купон; ставка; доход; погашение; частота; базис) | Возвращает цену за 100 рублей номинальной стоимости ценных бумаг для нерегулярного (короткого или длинного) первого периода купонных выплат. |
| ЦЕНАПОГАШ (дата согл; дата_вступл_в_силу; дата_выпуска; ставка; доходность; базис) | Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, по которым процент выплачивается в срок погашения (в срок вступления в силу одновременно с выкупом). |
| ЦЕНАПОСЛНЕРЕГ (дата_согл; дата_вступл_в_силу; Последняя выплата; ставка; доход; погашение; частота; базис) | Возвращает цену за 100 рублей нарицательной стоимости ценных бумаг для нерегулярного (короткого или длинного) последнего периода купона. |
| ЦЕНАСКИДКА (дата согл; дата_вступл_в_силу; скидка; погашение; базис) | Возвращает цену за 100 рублей номинальной стоимости ценных бумаг, на которые сделана скидка вместо выплаты процентов. |
| ЧИСЛКУПОН (дата_согл; дата_вступл_в_силу; частота; базис) | Возвращает количество купонов, которые могут быть оплачены между датой соглашения и сроком вступления в силу, округляемое до ближайшего целого купона. |
Таблица 1.5– Аргументы финансовых функций Excel анализа ценных бумаг
| Аргумент | Назначение аргумента |
| Базис | Используемый способ вычисления дня. |
| Дата_вступл_в_силу | Дата погашения ценной бумаги. |
| Дата_выпуска | Дата выпуска ценных бумаг. |
| Дата_согл | Дата приобретения ценной бумаги, дата инвестиций в ценные бумаги (более поздняя, чем дата выпуска). |
| Доход, доходность | Годовой доход по ценным бумагам. |
| Инвестиция | Объем инвестиции в ценные бумаги (цена приобретения). |
| Купон | Годовая ставка процента для купонов по ценным бумагам. |
| Номинал | Номинальная стоимость ценной бумаги (по умолчанию – 1000 руб.). |
| Первый_доход | Дата окончания первого периода (дата первой выплаты процентов по ценной бумаге). |
| Первый_купон | Дата первого купона для ценных бумаг в числовом формате. |
| Погашение | Выкупная стоимость ценных бумаг за 100 руб. номинальной стоимости. |
| Последняя_выплата | Дата последнего купона для ценных бумаг (последней выплаты процентов) . |
| Скидка | Скидка на казначейский вексель, учетная ставка в процентах к цене погашения. |
| Ставка | Годовая ставка процента на момент выпуска ценных бумаг. |
| Цена | Цена ценных бумаг за 100 руб. номинальной стоимости. |
| Частота | Количество выплат по купонам за год. |
Примечания.
1) Аргумент Частота (Периодичность) задается как число, принимающее следующие значения в зависимости от количества выплат по купонам за год:
1 – один раз в год (ежегодная выплата);
2 – два раза в год (полугодовая выплата);
4 – четыре раза в год (ежеквартальная выплата).
2) Аргумент Базис не является обязательным, однако играет важную роль, поскольку влияет на точность вычислений. В зависимости от способа вычисления временного периода аргумент Базис может принимать следующие значения:
0 – US(NASD) – американский стандарт, месяц равен 30, а год – 360 дням; принимается по умолчанию;
1 – фактический/фактический – фактическая длина месяца и года;
2 – фактический/360 – фактическая длина месяца, год равен 360 дням;
3 – фактический/365 – фактическая длина месяца, год равен 365 дням;
4 – европейский 30/360 – европейский стандарт, длина месяца равна 30 дням, длина года принимается 360 дней.
Следует отметить, что все даты должны быть выражены в числовом формате. Для этих целей служит функция ДАТА (год; месяц; день), которая преобразует заданную дату в числовой формат или, если дата задана текстом, то функция ДАТАЗНАЧ (дата_как_текст). Кроме того, Excel предоставляет возможность автоматически преобразовать дату в числовой формат, если в рассматриваемых функциях используется ссылка на ячейку, в которой содержится дата. Например, дату 3 января 2006 г. следует вводить в числовом формате как 38720.
Технология применения финансовых функций для анализа ценных бумаг
Date: 2022-10-19; view: 1885; Нарушение авторских прав
§
Постановка задачи.
Рассматривается возможность приобретения облигаций трех типов, каждая из которых с номиналом в 100 руб. и сроком погашения 9.10.2007 г. Курсовая стоимость этих облигаций на дату 25.07.2005 г. составила соответственно 90, 80 и 85 руб.
Годовая процентная ставка по купонам (размер купонных выплат) составляет:
для первой облигации 8 % при полугодовой периодичности выплат;
для второй облигации – 5 % при ежеквартальной периодичности выплат;
для третьей облигации – 10 % с выплатой 1 раз в год.
Расчеты ведутся в базисе фактический/фактический.
Провести анализ эффективности вложений в покупку этих облигаций, если требуемая норма доходности составляет 15%
Алгоритм решения задачи.
Чтобы оценить эффективность вложений в покупку каждой из облигаций, рассчитаем их годовую доходность, используя функцию ДОХОД:
ДОХОД (дата_согл; дата_вступл_в_силу; ставка; цена; погашение; частота; базис)
Для решения задачи построим на листе Excel таблицу, в ячейки которой введем исходные данные и формулы расчета требуемых величин (рис. 1.27).
Выполним также расчет доходности, непосредственно задавая значения аргументов в функции ДОХОД.
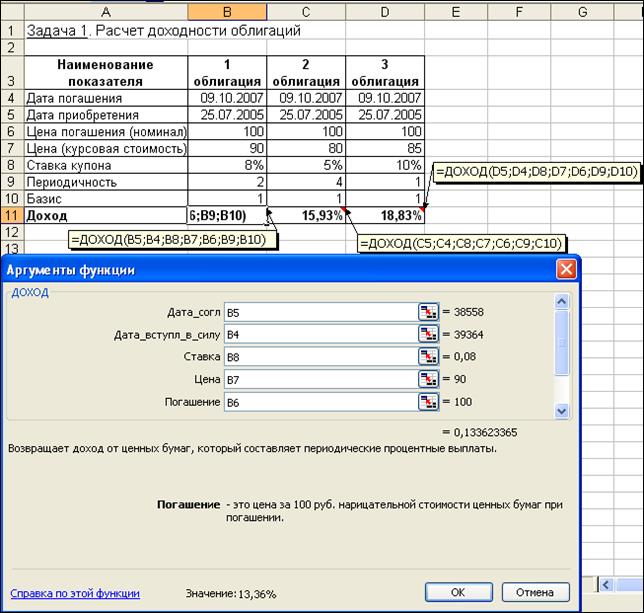
Рисунок 1.27– Применение функции ДОХОД для оценки доходности облигаций
Аргументы, содержащие даты, введем с помощью функции ДАТА (можно также указывать ссылки на ячейки, содержащие даты).
Для облигации первого типа:
=ДОХОД (ДАТА(2005;7;25);ДАТА (2007;10;9);8%;90;100;2;1)= 13,36%
Для облигации второго типа:
=ДОХОД (ДАТА(2005;7;25);ДАТА (2007;10;9);5%;80;100;4;1)= 15,93%
Для облигации третьего типа:
=ДОХОД (ДАТА(2005;7;25);ДАТА (2007;10;9);10%;85;100;1;1)= 18,83%
Результаты, полученные различными способами, совпадают.
Доходность по второй и третьей облигациям (15,93% и 18,83% соответственно) выше заданной нормы (15%), а по первой облигации (13,36%) – ниже. Следовательно, целесообразно покупать облигации второго и третьего типов.
Date: 2022-10-19; view: 1151; Нарушение авторских прав
§
§
§
Постановка задачи.
Определить стоимость ценной бумаги номиналом 1 000 руб. На ценную бумагу установлена скидка размером 11,5%. Дата приобретения ценной бумаги – 27 января 2006 г. Дата погашения – 10 января 2007 г. Расчеты выполнить в базисе Европейский/360.
Алгоритм решения задачи.
Определить стоимость ценной бумаги на дату покупки с учетом действующей скидки можно с помощью встроенной функции ЦЕНАСКИДКА, имеющей следующий формат:
=ЦЕНАСКИДКА (дата_согл; дата_вступл_в_силу; скидка; погашение; базис)
Функция при нахождении цены со скидкой реализует вычисления, вытекающие из формулы (4.18):
(1.19)
Используя функцию, найдем решение задачи, иллюстрация которого приведена на рис. 1.32. Как видно, на дату покупки стоимость ценной бумаги номиналом 1 000 руб. равна 890 руб. 43 коп. Различные варианты применения функции, а также формула (1.19) дают один и тот же результат:
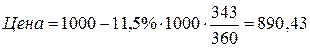
Задания для самостоятельной работы
1. Вексель номиналом 3 млн. руб. выдан 1.02.2006 г. сроком на 4 месяца. Учетная ставка составляет 15% годовых. Определить сумму, которую получит векселедатель, если при расчете используется стандартный базис 30/360.
2. Определить номинал векселя, выданного на 3 месяца при учетной ставке в 13% годовых, если векселедатель получил 17 тыс. руб.
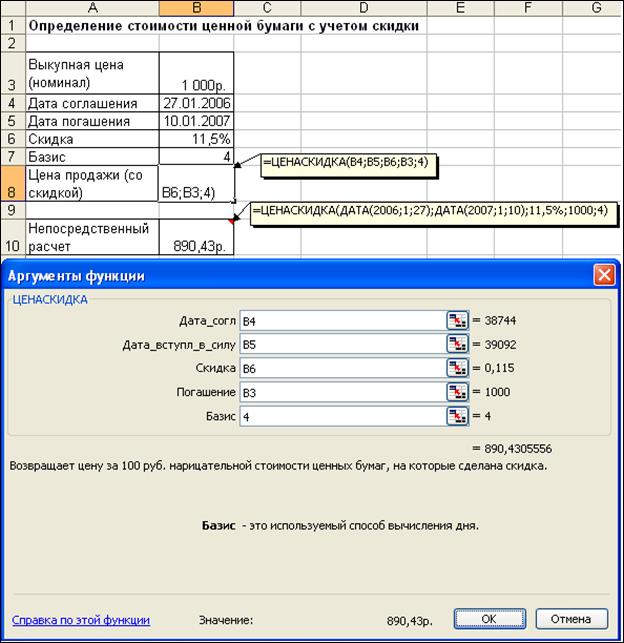
Рисунок 1.32– Иллюстрация использования функции ЦЕНАСКИДКА
3. Владелец векселя, выданного коммерческим банком, получит по нему через 4 года 180 000 руб. Определите, за какую сумму вексель был приобретен, если его доходность составляет 14% годовых.
4. Рассматривается возможность приобретения нескольких облигаций. Облигация № 1 имеет купон 13% годовых с выплатой 1 раз в год и продается по курсу 72,5. Облигация № 2 имеет купон 15% годовых с выплатой 1 раз в год и продается по курсу 65,5. Облигация № 3, имеющая купон 16 % годовых с выплатой 1 раз в год, продается по номиналу. Определите, какую облигацию следует приобрести?
5. Облигация номиналом 500 000 руб. с датой соглашения – 1.06.2005 г. и датой вступления в силу – 25.05.2006 г. имеет купон 7,5 % годовых при полугодовой периодичности выплат. Годовой доход составляет 8,5 %. Способ вычисления дня – фактический/360. Определить размер купонной выплаты и ежегодную продолжительность действия облигации.
6. Сберегательный сертификат коммерческого банка номиналом 200 тыс. руб. и сроком погашения через 6 месяцев был приобретен 12.02.2006 г. Процентная ставка по сертификату равна 30% годовых. Определить величину абсолютного дохода по сертификату на момент погашения при европейском способе начисления дня.
7. Номинальная стоимость обыкновенной акции 300 руб. Курс на вторичном рынке 330 руб. Дивиденды выплачены в размере 160 руб. Определить доходность акции.
8. Облигация номиналом 200 000 руб. и сроком погашения через 10 лет, имеет купон 5% годовых с выплатой 1 раз в полгода. Облигация приобретена через 3 года после выпуска. Дата выпуска – 20.03.2003 г. Определите цену покупки данной облигации и размер купонной выплаты, если требуемая норма доходности была равна 15%. Проанализируйте стоимость покупки облигации при разных вариантах норм доходности.
9. Рассматривается возможность приобретения облигации. Срок действия облигации с 15.06.2006 г. по 15.10.2006 г. Требуемая доходность равна 40 % годовых. Определите приемлемую стоимость для приобретения облигации на 20.09.2006 г.
10. Чеки казначейства имеют дату соглашения 14.08.2006 г. и дату погашения 14.12.2006 г. Норма скидки составляет 9%. Определить цену и доход по казначейскому чеку, а также годовой доход по казначейским чекам, эквивалентный доходу по облигациям.
11. На 15 июня текущего года имеется некоторый резерв наличности, равный 10 400 руб., который может быть внесен на депозит сроком на полгода или потрачен на покупку ценных бумаг, дата погашения которых намечена на конец года.
Депозитная ставка – 10,5% годовых. Информация о ценных бумагах приведена в таблице.
| Ценная бумага 1 | Ценная бумага 2 | Ценная бумага 3 | |
| Выкупная цена | 100,00р. | 200,00р. | 500,00р. |
| Дата соглашения | 16 июня | 15 июня | 16 июня |
| Дата погашения | 17 декабря | 19 декабря | 15 декабря |
| Цена продажи со скидкой | 95,00р. | 189,00р. | 472,00р. |
Найти скидку, действующую на указанные ценные бумаги, используя базис фактический/фактический. Определить, сколько каких ценных бумаг и на какую сумму может быть приобретено.
Рассчитать чистую прибыль в денежном эквиваленте для каждого из 4-х вариантов. Найти наиболее выгодный вариант вложения денег, обеспечивающий максимальную прибыль на каждый вложенный рубль.
Date: 2022-10-19; view: 1763; Нарушение авторских прав
§
Способы расчета амортизационных отчислений
Как известно, материальные фонды (недвижимость, транспортные средства, оборудование, станки, оргтехника и другие активы) имеют определенный срок службы. В процессе эксплуатации ресурс их вырабатывается, происходит износ и старение, соответственно уменьшается балансовая стоимость за счет амортизационных отчислений.
В соответствие с «Положением по бухгалтерскому учету (ПБУ 1-20)» амортизационные отчисления могут рассчитываться несколькими способами.
Линейный способ исходит из первоначальной стоимости или текущей (восстановительной) стоимости (в случае проведения переоценки) объекта основных средств, а также нормы амортизации, исчисленной исходя из срока полезного использования этого объекта.
Способ уменьшаемого остатка базируется на остаточной стоимости объекта основных средств на начало отчетного года и нормы амортизации, исчисленной исходя из срока полезного использования этого объекта и коэффициента ускорения, установленного в соответствие с законодательством.
Способ списания стоимости по сумме чисел лет срока полезного использования учитывает первоначальную стоимость или текущую (восстановительную) стоимость (в случае проведения переоценки) объекта основных средств и соотношение, в числителе которого число лет, остающихся до конца срока полезного использования объекта, а в знаменателе – сумма числа лет срока полезного использования объекта.
Способ списания стоимости пропорционально объему продукции (работ) обеспечивает начисление амортизационных отчислений исходя из натурального показателя объема продукции (работ) в отчетном периоде и соотношения первоначальной стоимости объекта основных средств и предполагаемого объема продукции (работ) за весь срок полезного использования объекта основных средств.
Финансовые функции расчета амортизации
Категория финансовых функций Excel обеспечивает расчет различных параметров при решении задач учета амортизации активов. Перечень таких функций соответственно представлен в табл. 1.6. В табл. 1.7 приведены описания аргументов функций.
Таблица 1.6– Финансовые функции учета параметров амортизации активов
| Формат | Назначение |
| АМОРУВ (стоимость; дата_приобр; первый_период; остаточ_стоимость; период; ставка; базис) | Возвращает при использовании французской системы бухгалтерского учета величину амортизации для каждого периода без учета зависимости коэффициента амортизации от периода амортизации актива. |
| АМОРУМ (стоимость; дата_приобр; первый_период; остаточ_стоимость; период; ставка; базис) | Возвращает при использовании французской системы бухгалтерского учета величину амортизации для каждого периода с учетом зависимости коэффициента амортизации от периода амортизации актива. |
| АПЛ (нач_стоимость; остаточ_стоимость; время_эксплуат) | Возвращает величину непосредственной амортизации актива за один период, рассчитанную линейным методом. |
| АСЧ (нач_стоимость; остаточ_стоимость; время_эксплуат; период) | Возвращает величину амортизации актива за данный период, рассчитанную методом «суммы (годовых) чисел». |
| ДДОБ (нач_стоимость; остаточ_стоимость; время_эксплуат; период; коэффициент) | Возвращает значение амортизации актива за данный период, используя метод двойного уменьшения остатка или иной явно указанный метод. |
| ПУО (нач_стоимость; остаточ_стоимость; время_эксплуат; нач_период; кон_период; коэффициент; без_переключения) | Возвращает величину амортизации актива для любого выбранного периода, в том числе для частичных периодов, с использованием метода двойного уменьшения остатка или иного указанного метода. |
| ФУО (нач_стоимость; остаточ_стоимость; время_эксплуат; период; месяцы) | Возвращает величину амортизации актива для заданного периода, рассчитанную методом фиксированного уменьшения остатка. |
Таблица 1.7– Описание аргументов функций
| Аргумент | Назначение аргумента |
| Базис | Используемый способ вычисления дня. |
| Без_переключения | Логическое значение; определяет, следует ли использовать линейную амортизацию в случае, когда амортизация превышает величину, рассчитанную методом снижающегося остатка. |
| Время_эксплуат, время_эксплуатации | Период амортизации, количество периодов, за которые собственность амортизируется. |
| Дата_приобр | Дата приобретения актива |
| Кон_период | Номер последнего периода, включенного в вычисления. |
| Коэффициент | Процентная ставка снижающегося остатка (по умолчанию – 2). |
| Месяцы | Количество месяцев в первом году эксплуатации (по умолчанию – 12). |
| Нач_период | Номер первого периода, включенного в вычисления. |
| Остаточ_стоимость, ост_стоимость | Остаточная стоимость актива в конце периода амортизации. |
| Первый_доход | Дата окончания первого периода. |
| Первый_период | Дата окончания первого периода. |
| Период | Период амортизации |
| Ставка | Процентная ставка за период амортизации. |
| Стоимость, нач_стоимость | Затраты на приобретение актива. |
Технология применения финансовых функций для расчета амортизационных отчислений
Date: 2022-10-19; view: 826; Нарушение авторских прав
§
§
Постановка задачи.
Организация сдает оборудование в аренду. Для более точного определения ее стоимости необходимо знать величину амортизационных отчислений, определяемых по методу двойного уменьшения остатка.
Переоценка оборудования перед сдачей в аренду определила его стоимость – 40 000 руб. Оставшийся срок эксплуатации – 3 года. Остаточная стоимость – 100 руб.
Рассчитать амортизационные отчисление на оборудование за первый и 365-й день аренды, первый, второй и пятый месяцы, первый год, а также некоторые периоды 2-го и 3-го годов.
Алгоритм решения задачи.
Поставленную задачу можно решить с помощью функций ПУО или ДДОБ, использующих метод двойного уменьшения остатка или иной явно указанный метод.
Функция ПУО возвращает величину амортизации актива для любого выбранного периода, в том числе для частичных и смежных периодов.
Функция ДДОБ возвращает значение амортизации актива за указанный период.
Форматы функций:
=ПУО (Нач_стоимость; Ост_стоимость; Время_эксплуатации; Нач_период;
Кон_период; Коэффициент; Без_переключения)
=ДДОБ (Нач_стоимость; Ост_стоимость; Время_эксплуатации;
Период; Коэффициент)
Описания функций требуют некоторого пояснения.
Аргументы Время_эксплуатации, Нач_период, Кон_период и Период всегда должны быть указаны в одних и тех же единицах.
Аргумент Коэффициент представляет собой процентную ставку снижающегося остатка. Если аргумент не указан (опущен), он полагается равным 2% (метод удвоенного процента со снижающегося остатка). Если нужно использовать другой метод вычисления амортизации, аргумент Коэффициент следует указать явно.
Аргумент Без_переключения представляет собой логическое значение, определяющее, следует ли при необходимости использовать линейную амортизацию. Если аргумент имеет значение ЛОЖЬ (или не задан), происходит автоматическое переключение на метод начисления линейной амортизации, если амортизация больше величины, рассчитанной методом снижающегося остатка. Если его значение ИСТИНА, переключение не происходит никогда.
Иллюстрация решения задачи с отображением введенных формул и полученных результатов приведена на рис. 1.36.
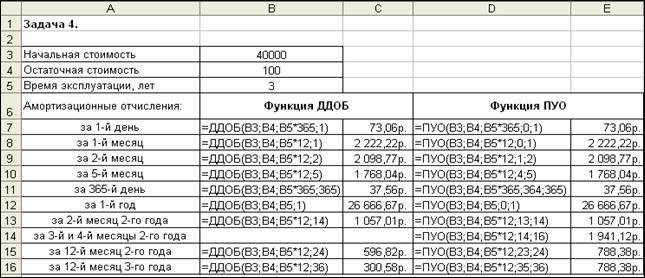
Рисунок 1.36– Применение функций ДДОБ и ПУО для вычисления амортизации
Как видно, для первых периодов амортизационные отчисления, найденные с помощью функций ДДОБ и ПУО совпадают. Совпадения будут до середины срока эксплуатации, когда балансовая стоимость оборудования сравняется с остаточной стоимостью вследствие использования метода двойного уменьшения остатка.
Для последних периодов результаты разные. Функция ПУО перешла на метод начисления линейной амортизации, а функция ДДОБ продолжает вычисления по формуле, которую она реализует:
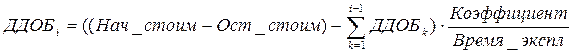(1.26)
Задания для самостоятельной работы
1. Приобретен объект основных средств стоимостью 200 000 руб. Срок полезного использования объекта – 5 лет. Используя линейный способ, рассчитать годовые амортизационные отчисления.
2. Приобретенная организацией за 25 000 долларов оргтехника имеет 6-летний срок полезного использования. Остаточная стоимость оргтехники в конце периода эксплуатации не будет превышать 500 долларов.
Применяя способ уменьшаемого остатка, рассчитать величину амортизационных отчислений за первый и второй годы.
Найти балансовую стоимость оргтехники на начало пятого года.
3. Применяя способ списания стоимости по сумме чисел лет срока полезного использования, найти годовые амортизационные отчисления для оборудования стоимостью 54 000 руб.Срок полезного использования оборудования – 8 лет. Остаточная стоимость – 1 800 руб.
Найти балансовую стоимость оборудования на начало каждого периода его эксплуатации.
4. На интенсивно используемое оборудование фирмы установлен коэффициент ускорения 3. Начальная стоимость оборудования – 125 000 руб. Остаточная стоимость – 5 000 руб. Установленный срок полезного использования – 5 лет.
Рассчитать амортизационные отчисления на оборудование за период со 2-го по 5-й месяц его эксплуатации.
Найти балансовую стоимость оборудования на начало 2-го года.
5. В марте текущего года принят на учет организации объект основных средств первоначальной стоимостью 210 000 руб. Срок полезного использования объекта – 7 лет.
Используя различные способы (линейный и уменьшаемого остатка), рассчитать величину амортизации объекта за все годы его эксплуатации. Определить балансовые стоимости объекта на начало календарных лет.
Результаты представить в графическом виде.
Date: 2022-10-19; view: 1452; Нарушение авторских прав
§
Табличный процессор Excel, безусловно, имеет широчайшие возможности по обработке данных, в том числе финансово-экономического характера. В данной книге авторы постарались эти возможности рассмотреть, иллюстрируя их необходимыми примерами и пояснениями. Однако какие-то моменты, безусловно, остались «за скобками». Что-то ускользнуло от внимания, другие вопросы были исключены преднамеренно, поскольку требовали включения в книгу сведений, непосредственно не имеющих отношения к финансово-экономической деятельности.
Практикум дает студентам опыт исследовательской работы, учит основам проектирования лабораторных моделей, знакомит с методами организации, планирования и обработки результатов экспериментов
Литература
1. Акинин П. В. Информационные системы в экономике. –М.: Кнорус, 2008. -256 с
2. Карлберг К. Бизнес-анализ с помощью Microsoft Excel. / Пер. с англ. –М.: Вильямс, 2005. -464 с.
3. Никольская Ю., Спиридонов А. Excel в помощь бухгалтеру и экономисту. –М.: Вершина, 2006. -256 с.
БОРЛАКОВА Амина Хисаевна
ПРОФЕССИОНАЛЬНО-ОРИЕНТИРОВАННЫЕ ЭКОНОМИЧЕСКИЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
Учебно-методическое пособие для выполнения
лабораторных работ для студентов 4 курса,
обучающихся по направлению подготовки
230700.62 «Прикладная информатика в экономике»
Корректор Чагова О. Х.
Редактор Батчаева Д. Р.
Сдано в набор 07.04.2022 г.
Формат 60х84/16
Бумага офсетная
Печать офсетная
Усл. печ. л. 4,18
Заказ № 1686
Тираж 100 экз.
Оригинал-макет подготовлен
в Библиотечно-издательском центре СевКавГГТА
369000, г. Черкесск, ул. Ставропольская, 36
А. Х. Борлакова
Date: 2022-10-19; view: 668; Нарушение авторских прав
