- Расчет ставки дисконтирования на основе модели wacc
- Алгоритм расчета дисконтированных денежных потоков от инвестнедвижимости
- Безрисковая ставка
- Вечная рента
- Дисконтирование аннуитетных платежей
- Другие варианты применения таблиц
- Кому придется использовать арендный стандарт в любом случае
- Модель оценки капитальных активов capm
- Понятие коэффициента дисконтирования и его значение
- Применение таблицы коэффициентов дисконтирования
- Примеры вычисления потоков денег с использованием фактора дисконта
- Расчет аннуитета — дисконтирование
- Расчет аннуитета — наращение
- Способ определения величины показателя
Расчет ставки дисконтирования на основе модели wacc
Оценка ставки дисконтирования на основе средней взвешенной стоимости капитала компании позволяет оценить стоимость всех источников финансирования ее деятельности. Этот показатель отражает фактические затраты компании на оплату заемного капитала, акционерного капитала, иных источников взвешенных по их доле в общей структуре пассива.
Если фактическая доходность компании выше WACC, тогда она генерирует некую добавленную стоимость для своих акционеров, и наоборот. Именно поэтому показатель WACC также рассматривают как барьерное значение требуемой доходности для инвесторов компании, то есть ставку дисконтирования.
Расчет показателя WACC осуществляется по формуле:
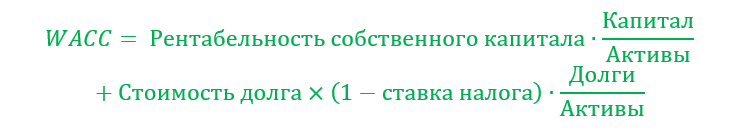
Конечно же, спектр методов обоснования ставки дисконтирования достаточно широк. Мы описали лишь основные способы, чаще всего применяемые инвесторами в той или иной ситуации. Как мы сказали ранее в нашей практике мы используем самый простой, но достаточно эффективный «интуитивный» способ определения ставки.
Выбор конкретного способа всегда остается за инвестором. Обучиться всему процессу принятия инвестиционных решений на практике можно на наших курсах в Школе разумного инвестирования. Глубоким методикам аналитики мы учим уже на втором уровне обучения, на курсах повышения квалификации практикующих инвесторов.
Если статья была для Вас полезной, поставьте лайк и поделитесь ей с друзьями!
Прибыльных Вам инвестиций!
Алгоритм расчета дисконтированных денежных потоков от инвестнедвижимости
Вопрос: Какой метод расчета ожидаемого денежного потока может быть применен для оценки ценности использования объекта инвестиционной недвижимости в банке?
Ответ: Оценка ценности использования объекта инвестиционной недвижимости может осуществляться методом дисконтирования денежных потоков (доходный метод).
Обоснование: Метод дисконтирования потоков денежных средств — это способ, используемый для оценки объектов недвижимости на основании анализа будущих доходов от эксплуатации объекта, приведенных к текущей стоимости, и позволяющий спрогнозировать величину будущих поступлений. В операциях дисконтирования денежный поток рассчитывается от будущего к настоящему.
Справочно
Дисконтирование (Present Value, PV) — определение стоимости денежных потоков, относящихся к будущим периодам.
Инвестиционная недвижимость используется банком для получения арендного дохода. В соответствии с п. 22 НСФО 40 для определения ценности использования объекта инвестиционной недвижимости рассчитывается текущая стоимость будущих потоков денежных средств, возникающих от его непрерывного использования и продажи по окончании срока полезного использования, с применением соответствующей ставки дисконтирования.
Справочно
Ценность использования объекта инвестиционной недвижимости — текущая стоимость будущих потоков денежных средств, возникновение которых ожидается от продолжающегося использования объекта инвестиционной недвижимости и его выбытия в конце срока полезного использования (оценивается по предполагаемой стоимости выбытия) <*>.
Сущность метода дисконтирования заключается в следующем:
1. Определяем прогнозируемый период, на протяжении которого происходит оценка поступающих денежных средств (не более пяти лет согласно п. 22 НСФО 40).
2. Рассчитываем чистый поток денежных средств (разница между доходами и расходами) по каждому году, включенному в прогнозируемый период, основываясь на данных бухгалтерских документов (отчета о движении денежных средств, отчета о прибылях и убытках и т.п.) и условиях договора аренды и т.п.
3. Определяемставку дисконтирования.
На заметку
Ставка дисконтирования должна отражать текущие рыночные оценки временной стоимости денежных средств и рисков, характерных для инвестиционной недвижимости на дату расчета суммы ее обесценения. В качестве ставки дисконтирования может применяться ставка рефинансирования Нацбанка <*>.
4. Осуществляем дисконтирование чистого денежного потока по годам (приводим финансовые потоки к первоначальному периоду), используя следующую формулу:

где
CF — денежные потоки во временные периоды «i», в которые поступают финансовые потоки;
i — год (шаг) расчета;
r — годовая ставка дисконта;
n — период прогнозирования.
Справочно
Потоки денежных средств — поступления и выплаты денежных средств, возникающие в процессе деятельности банка <*>.
При определении будущих потоков денежных средств, возникающих от использования и продажи инвестиционной недвижимости, не учитываются ожидаемые поступления или выбытия денежных средств вследствие <*>:
— будущей реструктуризации, относительно которой банком не признаны обязательства;
— будущих вложений в инвестиционную недвижимость;
— финансовой деятельности;
— выплат (поступлений) налога на прибыль.
5. Определяем суммарное значениенакопленного дисконтированного денежного потока за прогнозный период.
Положительное значение дисконтированного дохода означает, насколько возрастет стоимость вложенного капитала в результате реализации проекта с инвестиционной недвижимостью. Если значение дисконтированного дохода равно нулю — проект не принесет ни прибыли, ни убытков. Отрицательное же значение дисконтированного дохода покажет, какие убытки понесет банк от объекта инвестиционной недвижимости.
Для наглядности приведем пример расчета значений дисконтированных денежных потоков (DCF)(данные в таблице приведены условно):
Таблица
| Показатели | 1-й год | 2-й год | 3-й год | 4-й год | 5-й год |
| Чистый денежный поток (CF), дол. США (условно) | 20384 | 20985 | 21563 | 22412 | 22450 |
| Ставка дисконтирования (r), % <*> | 10 | 10 | 10 | 10 | 10 |
| Дисконтированный денежный поток (DCF), дол. США | 18531 <**> | 17343 <**> | 16213 <**> | 15351 <**> | 13944 <**> |
| ——————————— <*> В качестве ставки дисконтирования приведена ставка рефинансирования Нацбанка. <**> Расшифровка расчетов значений дисконтированных денежных потоков в каждом году: 1-й год: 18531 = 20384 / (1 0,10)1; 2-й год: 17343 = 20985 / (1 0,10)2; 3-й год: 16213 = 21563 / (1 0,10)3; 4-й год: 15351 = 22412 / (1 0,10)4; 5-й год: 13944 = 22450 / (1 0,10)5. | |||||
Сумма всех значений чистого дисконтированного денежного потока составит 81382 дол. США. (18531 17343 16213 15351 13944).
Так как итоговый показатель имеет положительное значение, можно говорить о привлекательности (доходности) использования объекта инвестиционной недвижимости.
Безрисковая ставка
Безрисковая ставка (или ставка доходности свободная от риска) – это ожидаемая норма доходности активов, по которым собственный финансовый риск равен нулю. Другими словами, это доходность по абсолютно надежным вариантам вложения денежных средств, например, по финансовым инструментам, доходность которых гарантирована государством.
Акцентируем внимание на том, что даже для абсолютно надежных финансовых вложений абсолютный риск не может отсутствовать (в этом случае и ставка доходности стремилась бы к нулю). В безрисковую ставку как раз и заложены факторы рисков самой экономической системы, рисков, на которые не может повлиять ни один инвестор: макроэкономические факторы, политические события, изменения законодательства, чрезвычайные антропогенные и природные события и т.п.
Следовательно, безрисковая ставка отражает минимально возможную доходность, приемлемую для инвестора. Безрисковую ставку инвестор должен выбрать для себя самостоятельно. Можно рассчитывать среднюю величину ставки из нескольких вариантов потенциально безрисковых инвестиций.
При выборе безрисковой ставки инвестор должен учитывать сопоставимость своих вложений с безрисковым вариантом по таким критериям как:
Масштаб или суммарная стоимость инвестиций.
Инвестиционный период или горизонт инвестирования.
Физическая возможность осуществления вложений в безрисковый актив.
Эквивалентность номинирования ставок в валюте, и другие.
В качестве безрисковой рекомендуется выбирать процентную ставку на уровне следующих вариантов:
Ставки доходности по срочным рублевым депозитам в банках высшей категории надежности. В России к таким банкам относят Сбербанк, ВТБ, Газпромбанк, Альфа-Банк, Россельхозбанк и ряд других, перечень которых можно посмотреть на сайте Центрального банка РФ. При выборе безрисковой ставки данным способом необходимо учитывать сопоставимость срока инвестирования и периода фиксации ставки по вкладам.
Приведем пример. Воспользуемся данными сайта ЦБ РФ. По состоянию на август 2022 г. средневзвешенные процентные ставки по депозитам в рублях на срок до 1 года составили 6,77%. Эта ставка и является безрисковой для большинства инвесторов, осуществляющих инвестирование на срок до 1 года;
Уровень доходности по российским государственным долговым финансовым инструментам. В этом случае безрисковая ставка фиксируется в виде доходности по облигациям федерального займа (ОФЗ). Эти долговые ценные бумаги эмитируются и гарантируются Министерством финансов РФ, поэтому считаются самым надежным финансовым активом в РФ. При сроке до погашения 1 год ставки по ОФЗ составляют на текущий момент от 7,5% до 8,5%.
Уровень доходности по иностранным государственным ценным бумагам. В данном случае безрисковая ставка приравнивается к доходности государственных облигаций США со сроками обращения от 1 года до 30 лет. Традиционно экономика США международными рейтинговыми агентствами оценивается на наивысшем уровне надежности, а, следовательно, доходность их государственных облигаций и признается безрисковой. Однако следует учитывать, что безрисковая ставка в этом случае номинирована в долларовом, а не рублевом эквиваленте. Поэтому, для анализа инвестиций в рублях необходима дополнительная корректировка на так называемый страновой риск;
Уровень доходности по российским государственным еврооблигациям. Такая безрисковая ставка также номинирована в долларовом эквиваленте.
Ключевой ставки ЦБ РФ. На момент написания этой статьи ключевая ставка составляет 9,0%. Считается, что эта ставка отражает цену денег в экономике. Рост этой ставки влечет удорожание кредита и является следствием нарастания рисков. Применять этот инструмент следует с большой осторожностью, так как это все-таки директивный, а не рыночный показатель.
Ставки рынка межбанковского кредитования. Эти ставки носят индикативный характер и более приемлемы по сравнению с ключевой ставкой. Мониторинг и перечень этих ставок опять же представлен на сайте ЦБ РФ. Например, по состоянию на август 2022 г.: MIACR 8,34%; RUONIA 8,22%, MosPrime Rate 8,99% (1 день); ROISfix 8,98% (1 неделя). Все эти ставки носят краткосрочный характер и представляют доходность по операциям кредитования наиболее надежных банков.
Вечная рента
Вечная рента — это аннуитет, платежи которого продолжаются в течение неограниченного срока. Другими словами – это серия одинаковых платежей, которая продолжается вечно. Такой вариант возможен, если, например, у вас есть вклад в банке, вы снимаете только ежегодные проценты, а основная сумма вклада остается нетронутой. Тогда, если ставка процента по вкладу не меняется, у вас будет так называемая вечная рента.
В викторианскую эпоху все английские аристократы жили на проценты со своего капитала. Чем больший капитал лежал в банке, тем большие средства можно было потратить на жизнь и при этом не работать. Капитал переходил по наследству, и теоретически (если бы не было банкротств банков, войн и инфляции) так могло бы продолжаться вечно.
Будущая стоимость вечной ренты не имеет смысла, так как платежи продолжаются неограниченно долго. Однако текущая стоимость вечной ренты является конечной суммой, которую можно вычислить по формуле:
PV = платеж/R,
где R – это банковская ставка %, PV — текущая стоимость
Например, если хочется снимать со счета проценты в сумме 500,000 рублей в год, а годовая банковская ставка составляет 8%, то это значит, что сумма вклада на банковском счете должна быть равна:
500,000/0,08 = 6,250,000 рублей (PV).
В этом случае (если у банка не отберут лицензию или банк не обанкротится сам) можно снимать такие проценты постоянно на протяжении неограниченного периода времени. Единственное, что может нарушить такую идиллическую картину, — это инфляция, благодаря которой деньги обецениваются. Поэтому с течением времени снимаемые проценты будут приносить всё меньше материальных благ.
Философское отступление для тех, кто дочитал до этого места.
Чтобы рента была вечной, нужно сохранять капитал, с которого мы получаем эту ренту. Этот закон действует не только в финансовом мире. Человечество живет за счет природной ренты – оно пользуется ресурсами планеты, которые, к сожалению, исчерпаемы. Если брать от природы слишком много, природная рента иссякнет. Истощение земных ресурсов происходит на наших глазах.
При традиционном рыболовстве рыбу ловили понемногу, но это могло продолжаться вечно. Индустриальные города требуют рыбу определенного сорта и качества, для вылова которой применяется промышленный рыболовный флот. Крупные суда гонятся лишь за прибылью и не уважают океан.
«Мир достаточно велик, чтобы удовлетворить нужды любого человека, но слишком мал, чтобы удовлетворить человеческую жадность» Махатма Ганди
Планета Земля – это наш единственный дом. Думаем ли мы об этом?
Дисконтирование аннуитетных платежей
ПРИМЕР 1. Необходимо выбрать наиболее выгодный вариант:
А) получить 40,000 долларов сегодня или
(Б) 5 раз по 10,000 долларов в конце каждого из следующих 5 лет.
Банковская ставка для получения кредита на данный срок составляет 10%.
На первый взгляд вариант (Б) в сумме лучше (5 х 10,000 = 50,000), чем 40,000 долларов. Но действительно ли это так? Ведь мы знаем, что у денег есть еще и «временная» стоимость. Чтобы сравнить эти два варианта между собой, надо привести их к одному моменту времени (к моменту «сейчас»), поскольку стоимость денег в разные моменты времени различна. В данном случае надо продисконтировать аннутитетный денежный поток (Б), т.е. рассчитать его сегодняшнюю стоимость.
Для начала давайте вспомним, как выглядит формула дисконтирования:
PV = FV х 1/(1 R) n
Future value (FV) – будущая стоимость Present value (PV) – текущая (дисконтированная/приведенная) стоимость. R – ставка процента (норма доходности, требуемая инвестором), N – число лет от даты в будущем до текущего момента
Коэффициенты дисконтирования, используемые для нашего примера 1/(1 R) n — это 0.9091, 0.8264 и т.д. Только эти вычисления придется повторить 5 раз и сложить. Если продисконтировать (то есть привести к текущему моменту) каждую сумму отдельно, то получится вот такая таблица:
10,000 х 0,9091 = 9,09110,000 х 0,8264 = 8,26410,000 х 0,7513 = 7,51310,000 х 0,6830 = 6,83010,000 х 0,6209 = 6,209Итого: 37,907
Здесь сумма платежа умножена на соответствующий каждому году коэффициент дисконтирования. В итоге, пять платежей по 10,000 долларов в конце каждого года с учетом дисконтирования стоят 37,907 долларов, что немного меньше, чем 40,000 сегодня. Следовательно, при ставке 10%, 40,000 долларов сегодня будет выгоднее, чем предложенный аннуитет 5 лет по 10,000 долларов.
Формулу дисконтированной стоимости аннуитета можно записать следующим образом:
PV = PMT х [1/(1 R) 1 1/(1 R) 2 1/(1 R) 3 1/(1 R) 4 1/(1 R) 5 ] = 10,000 х (0.9091 0.8264 0.7513 0.6830 0.6209) = 10,000 х 3.7907 = 37,907
где PMT (от английского payment) – это сумма аннуитетного платежа.
Как Вы могли заметить, вместо того чтобы дисконтировать каждую сумму отдельно, можно сложить все коэффициенты дисконтирования и умножить только один раз. Результат сложения коэффициентов дисконтирования за 5 лет называется коэффициентом аннуитета. В данном примере коэффициент аннуитета равен 3,7907.
Таким образом, для нахождения текущей стоимости аннуитетов необходимо разовый платеж умножить на коэффициент аннуитета (10,000*3,7907 = 37,907).
Итак, мы разобрали пример с аннуитетными платежами в конце каждого года (постнумерандо) .
ПРИМЕР 2. Давайте немного изменим условия нашего примера. Необходимо выбрать наиболее выгодный вариант:
А) получить 40,000 долларов сегодня или
Б) 5 раз по 10,000 долларов в начале каждого из следующих 5 лет.
Это будет так называемый аннуитет пренумерандо.
В данной ситуации, так как первый платеж производится в начале года, то самый важный нюанс, о котором надо помнить, это то что, первый платеж не надо дисконтировать (т.е. приводить к настоящему моменту). Другими словами, для первого платежа используется коэффициент дисконтирования равный единице.
10,000 х 1.000 = 10,00010,000 х 0.9091 = 9,09110,000 х 0.8264 = 8,26410,000 х 0.7513 = 7,51310,000 х 0.6830 = 6,830Итого: 41,698
Следовательно, предложенный аннуитет 5 лет по 10,000 в начале года будет выгоднее, чем 40,000 сегодня при ставке 10%.
Формула дисконтированной стоимости аннуитета:
PV = PMT PMT х [1/(1 R) 1 1/(1 R) 2 1/(1 R) 3 1/(1 R) 4 ] = 10,000 10,000 х (0.9091 0.8264 0.7513 0.6830) = 10,000 10,000 х 3.1698 = 41,698
Обратите внимание, что в данном примере мы определили коэффициент аннуитета для четырех отложенных во времени платежей, а не для пяти, а первый платеж не дисконтировали.
Как видно из данных примеров, большое значение имеет момент, когда производятся платежи: в начале или в конце периода. Поэтому, если нужно рассчитать дисконтированную стоимость аннуитетных денежных потоков, желательно рисовать шкалу времени, на которой отметить суммы и коэффициенты, соответствующие каждому периоду.
Источник
Другие варианты применения таблиц
По тому же алгоритму, что и таблицы дисконтирования, составляются таблицы, позволяющие рассчитать наращение капитала во времени. Здесь коэффициенты выше единицы, поскольку вычисление направлено по времени вперед и текущая стоимость потока приводится к будущему периоду.
Снова попробуем решить задачу. Бизнесмену предложили два варианта получения одолженных денег в сумме 50 тысяч долларов:
- получить их прямо сейчас;
- получить через 5 лет сумму в 90 тысяч долларов.
Нужно подсчитать, какой вариант более выгоден, исходя из стандартной банковской ставки 10%. Берем из интернета готовую таблицу или составляем ее самостоятельно в программе Excel.
Эта задача решается очень просто. В нужной ячейке таблицы находится требуемое значение 1,6105, которое подставляется в формулу наращения FV =PV * (1 R) n .
FV = 50000 * 1,6105
FV = 80525
Мы получаем приведенную стоимость сегодняшних 50 тысяч долларов через 5 лет в размере 80525 долларов при исходном условии, что партнер гарантирует через тот же срок возвращение средств в размере 90 тысяч. Таким образом, гораздо выгоднее согласиться на второй вариант из предложенных и через 5 лет получить 90 тысяч.
Удобны для применения табличные материалы и для расчета аннуитетных платежей, то есть предполагающих одинаковые выплаты в начале или конце равных отрезков времени. Такие ситуации часто возникают, когда люди берут банковские кредиты. Мы же снова рассмотрим пример, сходный с предыдущей задачей.
У нас снова есть кредитор, которому предлагают два варианта возврата данных в долг денег:
- получить свои 50 тысяч долларов сразу;
- получать ежегодно по 12 тысяч в течение 5 лет.
На первый взгляд, заманчивое предложение, можно выиграть дополнительно 10 тысяч, не прикладывая особых усилий. Однако стоит проверить это по формулам дисконтирования. Норма дисконта составляет 10%. Если использовать простую табличку, то нужно ежегодные суммы множить на соответствующие факторы, а затем все их сложить.
12000 * 0,9091 = 10909,2
12000 * 0,8264 = 9916,8
12000 * 0,7513 = 9015,6
12000 * 0,6830 = 8196,0
12000 * 0,6209 = 7450,8
В сумме мы получим 45488,4 долларов, то есть предложенный вариант получения денег частями невыгоден, поэтому лучше получить их сейчас и вложить в перспективный бизнес или просто разместить на депозитном счете.
При использовании специальной таблицы, считать придется намного меньше. Здесь достаточно найти нужный показатель, применение которого будет аналогично приведенным ранее расчетам. Сумму ежегодного платежа нужно умножить на коэффициент: 12000 * 3,7908 = 45489,6 долларов, что практически равно сумме расчетов по отдельным годам.
Из всего сказанного можно сделать логичный вывод: использование специальных таблиц с заранее просчитанными коэффициентами позволяет быстро и легко производить финансовые расчеты, связанные с временным фактором, в обоих направлениях.
Исключение здесь составляют только крупные инвестиционные проекты, которые могут быть подвержены многочисленным трудно прогнозируемым рискам. Для них более приемлемыми являются экспертная или кумулятивная оценка нормы дисконта.
Источник
Кому придется использовать арендный стандарт в любом случае
Начиная с 01.01.2022 с ФСБУ 25/2022 «Бухгалтерский учет аренды» придется разбираться каждому бухгалтеру, так как этот стандарт становится обязательным. ФСБУ 25/2022 утвержден приказом Минфина России от 16.10.2022 № 208.
Прежде чем показать пример дисконтирования арендных платежей, разберемся, все ли обязаны использовать в работе новшества.
Подробно обо всех нюансах нового стандарта можно прочитать в статье «Новое ПБУ «Аренда».
Бухгалтеры госсектора могут спать спокойно: они не обязаны применять новый стандарт. Кроме того, при соблюдении определенных условий данный стандарт может не применяться и иными хозсубъектами.
Чтобы определить перечень освобожденных от его применения, для начала определим ключевые термины арендного бухстандарта.
ВАЖНО! ФСБУ 25 определяет, как отражать в бухучете полученное или предоставленное во временное пользование имущество.
Не знаете, как перейти на применение ФСБУ 25/2022? Оформите пробный бесплатный доступ к К и получите подробный алгоритм действий для того, чтобы корректно начать применять ФСБУ 25/2022.
Что такое объект аренды:
Арендный бухстандарт не применяется для следующих ситуаций:
Рассмотрим дополнительные условия, при которых можно не применять новый арендный стандарт:
Сразу оговоримся, что если договор аренды помещения заключен на 11 месяцев, то он не относится к п. 1 (срок аренды не превышает 12 месяцев), так как данную сделку следует оценивать в целом, исходя не из «бумажного» срока аренды, а из фактического.
Подробнее об этом можно прочитать здесь.
Далее рассмотрим, что же такое дисконтирование арендных платежей, и приведем пример расчета ставки дисконтирования по аренде.
Ранее мы уже писали о новых стандартах, которые обязательны с 2022 года:
Модель оценки капитальных активов capm
Автором этой модели является нобелевский лауреат по экономике У. Шарп. Логика этой модели не отличается от предыдущей (ставка доходности складывается из безрисковой ставки и рисков), различен способ оценки инвестиционного риска.
Эта модель считается фундаментальной, поскольку устанавливает зависимость доходности от степени ее подверженности внешним факторам рыночного риска. Эта взаимосвязь оценивается через так называемый «бета»-коэффициент, по сути являющийся мерой эластичности доходности актива к изменению средней рыночной доходности аналогичных активов на рынке. В общем виде модель САРМ описывается формулой:

Где β – «бета»-коэффициент, мера систематического риска, степень зависимости оцениваемого актива от рисков самой экономической системы, а среднерыночная доходность – это средняя доходность на рынке аналогичных инвестиционных активов.
Если «бета»-коэффициент выше 1, то актив «агрессивный» (более доходный, меняется быстрее рынка, но и более рискованный по отношению к аналогам на рынке). Если «бета»-коэффициент ниже 1, то актив «пассивный» или «защитный» (менее доходный, но и менее рискованный). Если «бета»-коэффициент равен 1, то актив «безразличный» (доходность его меняется параллельно рынку).
Рассчитать «бета»-коэффициент инвестор может самостоятельно, на основе методов математической статистики. Как это делать и специальную программу для этого мы даем в курсе «Секретное оружие портфельных инвесторов».
Понятие коэффициента дисконтирования и его значение
Коэффициент дисконтирования денежных потоков – это цифровой показатель, используя который можно понять, сколько денег удастся получить через определенное время с учетом временного фактора и возможного риска. Таким образом, производится приведение потоков денег в будущем к состоянию на день анализа.
В бизнес-проектировании «деньги сейчас» всегда предпочтительнее, чем «деньги потом», поскольку их можно вложить в другое дело и получить доход или разместить на банковском депозите и получать фиксированный процент. Следовательно, перед вложением инвестор должен быть уверен, что в течение жизненного цикла проекта он не только не потеряет от удешевления денег, но и сможет получить прибыль.
Интервал времени, на протяжении которого реализуется начинание и приносит прибыль участникам, устанавливается заранее. Он, как правило, определяется по нормативным срокам применения установленного оборудования, после чего технические возможности производства продукции исчерпываются. От правильного определения временных рамок начинания во многом зависит объективность вычислений.
Значение коэффициента дисконтирования используется в разных ситуациях:
- оценка эффективности экономической деятельности какой-либо фирмы;
- расчет эффективности инвестиционного проекта;
- рассмотрение альтернативных вариантов вложения средств как между разными инициативами, так и внутри одного предприятия (выбор наиболее перспективного пути развития);
- многосторонние расчеты и кредитование.
Этот показатель фактически устанавливает некий норматив издержек или поступления капитала при вложении его в другое начинание. Иными словами, коэффициент (или фактор) дает возможность определить размер процента, на который следует множить ожидаемые доходы для того, чтобы выйти на конкретную сумму применительно к сегодняшнему состоянию.
Применение таблицы коэффициентов дисконтирования
Для большей наглядности, попробуем решить простую бизнес задачу по приведению денежного потока, используя обычный метод. Инвестор вкладывает в инвестиционный проект 500 тысяч долларов с перспективой получить через 5 лет 1 миллион долларов одноразовым платежом. Ставка дисконтирования составляет 12%.
Производим вычисления фактора по стандартной формуле Kd =1 / (1 R) n .
Kd =1 / (1 0,12) 5
Kd =1 / 1,7623
Kd =0,5674
Следовательно, каждый вложенный в предложенный замысел доллар будет стоить 56,74 цента. Далее несложно просчитать приведенную стоимость денег, используя формулу PV = FV * 1/(1 R) n .
PV = 1000000 * 0,5674
PV = 567400
В итоге имеем понимание того, что проект этот является потенциально прибыльным, однако реальный размер прибыли выглядит не так впечатляюще, как при оценке до дисконтирования. Учет удешевления денег позволяет принимать более взвешенные решения.
Для упрощения расчетов в большинстве случаев применяется таблица дисконтирования, в которой один множитель – это размер процентной ставки (указан в столбцах), а второй – период времени (в строках). На их пересечении рассчитаны коэффициенты с точностью до четырех знаков после запятой.
В нашем примере нет необходимости вычислять коэффициент с риском ошибиться. К тому же мы взяли для рассмотрения максимально простые исходные условия, поскольку если выплаты будут производиться частями через определенные периоды времени (ежеквартально или ежегодно), то расчеты станут сложнее.
Если под рукой имеются таблицы (а их легко найти в интернете), то на пересечении столбца с показателем «12%» и строки с показателем «5» мы видим ячейку со значением «0,5674», что точно соответствует произведенным нами выше вычислениям. Также здесь можно буквально за несколько секунд определить, что за тот же период при ставке в 10% вложенные полмиллиона будут стоить 620,9 тысяч долларов, а при ставке 15% — лишь 497,2 тысяч долларов, то есть проект становится потенциально убыточным.
Примеры вычисления потоков денег с использованием фактора дисконта
Рассмотрим пример расчета. Бизнесмен вкладывает в новый шестилетний проект 800 тысяч рублей. Согласно с представленным инициатором бизнес-планом, через 6 лет он сможет единоразовым платежом получить 1,5 миллиона рублей. Кумулятивным способом определена ставка дисконтирования 12%, при этом процент нормы дисконта записывается при подсчете в виде части от единицы (0,12). Теперь, используя стандартную формулу, можно посчитать величину фактора:
Kd =1 / (1 0,12) 6
Kd =1 / 1,9738
Kd =0,5066
Мы получили коэффициент приведения в размере 0,5066. После этого по формуле дисконтирования рассчитываются показатели стоимости приведенного денежного потока:
PV = FV * 1/(1 R)n.
PV = 1500000 * 0,5066
PV = 759900
Из полученного результата можно сделать неутешительный для инвестора вывод, что при таких стартовых условиях ему не следует ожидать не только прибыли, но и даже простого возврата вложенных денег. Следовательно, от такого предложения нужно отказаться или же предложить изменить основные условия проекта, если это приемлемо (сократить срок реализации или уменьшить норму дисконта).
Предположим, что норма дисконта в нашем примере снижена до 10%. В таком случае значение коэффициента составит 0,5645, а приведенный поток денег возрастет до 846750 рублей, что сделает проект прибыльным. Аналогичная ситуация возникает и в случае сокращения срока внедрения до 5 лет при ставке 12%: фактор будет 0,5674, а поток – 851100 рублей.
Следует отметить, что для того, чтобы определить коэффициент дисконтирования, нет необходимости каждый раз погружаться в математические формулы. Для упрощения этого задания разработана и широко применяется на практике таблица коэффициентов дисконтирования.
Она построена по стандартной схеме, как таблицы Пифагора или Брадиса, то есть на одной оси указаны размеры процентных ставок, на другой – временные отрезки. Для нахождения нужного показателя достаточно найти ячейку, где они пересекаются, в ней содержится величина коэффициента с точностью до десятитысячных (до четвертого знака после запятой).
Все приведенные выше значения коэффициентов, взяты из этой таблицы. Это значительно ускоряет расчеты и дает возможность без лишних усилий просчитывать альтернативные варианты развития событий.
Мы рассматривали задачу, в которой предусматривалась выплата денег одним платежом после окончания проекта. На практике, гораздо чаще встречаются ситуации, когда выплаты производятся ежегодно. Тогда для корректности расчетов необходимо находить коэффициент приведения для каждого года отдельно.
Применяя формулу годовых расчетов, можно находить коэффициенты отдельно по каждому периоду, а затем просуммировать их:
| CF1 | CF2 | CFN | |||
| NPV = | —— | —— | … | —— | |
| (1 R) | (1 R)2 | (1 R)6 |
PV = 227272 206611 187828 170765 155279 141083 = 1088838 рублей.
Если же использовать таблицу коэффициентов аннуитетных платежей, то достаточно будет размер среднегодового платежа умножить на фактор, указанный в нужной ячейке таблицы (в данном случае это 4,3553).
PV = 250000 * 4,3553 = 1088825 рублей
Таким образом, мы видим, что показатель, найденный по формуле, практически аналогичен величине, определенной при помощи таблиц (1088838 против 1088825).
Расчет аннуитета — дисконтирование
ПРИМЕР 1. Возьмем абстрактный пример. Допустим, вам надо выбрать, что лучше:
- (А) получить 100,000 долларов сегодня или
- (Б) 5 раз по 25,000 долларов в конце каждого из следующих 5 лет.
В сумме 5 * 25,000 = 125,000, что вроде бы лучше, чем 100,000 долларов. Но так ли это? Ведь у денег есть еще и «временная» стоимость. Банковская ставка в данный момент в данной стране, допустим, равна 10%.
Вариант (Б) представляет собой простой вариант аннуитета. Только не все знают, что это именно так называется. Чтобы сравнить эти два варианта между собой (что выгоднее?), надо привести их к одному моменту времени, поскольку стоимость денег в разные моменты времени различна.
В данном случае надо продисконтировать аннутитетный денежный поток (Б), т.е. рассчитать его сегодняшнюю стоимость. Если дисконтированная стоимость аннуитета будет больше, чем 100,000 долларов, значит, второй вариант выгоднее при данной ставке процента.
В предыдущей статье мы научились дисконтировать одиночную сумму. Те же вычисления можно сделать и в этот раз, только придется повторить их 5 раз.
На данной шкале времени кроме платежа в сумме 25,000 нанесены соответствующие каждому периоду коэффициенты дисконтирования. Таблица коэффициентов дисконтирования приведена в предыдущей статье про дисконтирование.
Если продисконтировать (то есть привести к текущему моменту) каждую сумму отдельно, то получится вот такая табличка:
- 25,000*0,9091 = 22,727
- 25,000*0,8264 = 20,661
- 25,000*0,7513 = 18,783
- 25,000*0,6830 = 17,075
- 25,000*0,6209 = 15,523
- Итого: 94,770
Здесь сумма платежа умножена на соответствующий каждому году коэффициент дисконтирования. В целом пять платежей по 25,000 в конце каждого года с учетом дисконтирования стоят 94,770, что несколько меньше, чем 100,000 сегодня. Следовательно, 100,000 сегодня при ставке 10% будет выгоднее, чем предложенный аннуитет 5 лет по 25,000.
Этот пример важен не только, чтобы еще раз продемонстрировать временную стоимость денег. Из таблицы становится ясно, как можно упростить вычисление дисконтированной стоимости аннуитета. Вместо того чтобы дисконтировать каждую сумму отдельно, можно сложить все коэффициенты дисконтирования и умножить только один раз:
25,000*(0,9091 0,8264 0,7513 0,6830 0,6209) что аналогично 25,000*3,7908=94,770
Из этого примера легко вывести математическую формулу расчета дисконтированной стоимости аннуитета.
Сначала вспомним, как выглядит формула дисконтирования:
PV = FV*1/(1 R) n
Коэффициент дисконтирования равен 1/(1 R) n — это 0,9091, 0,8264 и т.д. в нашем примере.
Формула аннуитета (для расчета дисконтированной стоимости аннуитетных денежных потоков)
PV = FV*[1/(1 R) 1 1/(1 R) 2 1/(1 R) 3 1/(1 R) 4 1/(1 R) 5 ]
И так далее, в зависимости от того, сколько у вас периодов времени.
Выражение в квадратных скобках можно представить математически, но вряд ли это нужно большинству людей. Это называется коэффициент аннуитета, или аннуитетный коэффициент дисконтирования, точное название не столь важно. В примере выше этот коэффициент равен 3,7908.
Гораздо полезнее уметь пользоваться таблицами таких коэффициентов для расчета приведенной (дисконтированной) стоимости аннуитетного денежного потока. Такие таблицы позволяют быстро решать простые задачи на дисконтирование аннуитетов. Пример такой таблицы дисконтирования приведен ниже:
Если кому-то нужна точная формула аннуитета, точнее формула коэффициента дисконтирования аннуитета, то вот она:
Коэффициент дисконтирования аннуитета: 1/R — 1/(R*(1 R) n )
Дисконтированная стоимость аннуитета: PV= платеж умножить на коэффициент
Расчет аннуитета — наращение
В примере выше мы считали дисконтированную стоимость денежного потока. То есть приводили стоимость денежного потока к текущему моменту времени. Можно решать и обратную задачу – узнать будущую стоимость аннуитета (аннуитетного денежного потока).
ПРИМЕР 2. В нашем первом примере мы можем посчитать будущую стоимость обоих вариантов. Если перевести из области чистой математики в жизненную плоскость, то надо выбрать, что лучше:
- (А) положить сегодня 100,000 долларов в банк под 10% годовых или
- (Б) в конце каждого года делать взносы в сумме 25,000.
Для первого варианта можно воспользоваться таблицей коэффициентов наращения (она есть в предыдущей статье).
Для варианта (А) будущая стоимость считается просто: $100,000 через 5 лет будут равны 100,000*1,6105 = $161,050
Для варианта (Б) ситуация несколько сложнее.
Мы хотим узнать, сколько будет у нас на счете через 5 лет, если мы будем откладывать 25,000 в конце каждого года. То есть мы сделаем последний взнос и сразу же посчитаем, сколько мы накопили. Чтобы не ошибиться, лучше подписать коэффициенты наращения, соответствующие каждому году, на шкалу времени.
Первый платеж будет сделан в конце первого года, это значит, что через 5 лет по нему будут наращены проценты только за 4 года. Соответственно, по второму платежу мы получим проценты за 3 года, по третьему – за два года, по четвертому – за один год, и, наконец, положив деньги в пятый раз, проценты по последнему взносу еще нее возникнут (то есть надо будет умножить на 1,10 в нулевой степени!)
25,000*(1,1) 4 25,000*(1,1) 3 25,000*(1,10) 2 25,000*(1,10) 1 25,000 (1,10) 0 что равно
25,000*1,4641 25,000*1,3310 25,000*1,2100 25,000*1,1000 25,000*1 = 25,000*6,1051 = 152,628
Будущая стоимость аннуитета (вариант Б) равняется $152,628, что существенно меньше, чем $161,050 (вариант А). Это означает, что выгоднее внести на банковский счет 100,000 долларов сегодня, чем делать взносы 25,000 в конце каждого из 5 следующих лет. Данный вывод справедлив для банковской ставки 10% годовых.
Для расчета будущей стоимости аннуитетных денежных потоков тоже имеются таблицы коэффициентов. В данном случае этой таблицей можно пользоваться для расчета аннуитетов с платежами в конце временного интервала (т.е. постнумерандо).
Для любителей математики формула аннуитета для расчета его будущей стоимости выглядит так:
Коэффициент наращения аннуитета: FV = платеж умножить на коэффициент,
где коэффициент равен: [(1 R) n – 1]/R
Это был аннуитет с платежами в конце каждого года (постнумерандо).
ПРИМЕР 3.Можно рассмотреть и другой пример. Сколько мы накопим на счете в банке, если будем вносить по 25,000 в начале каждого года, а не в конце? Это будет так называемый аннуитет пренумерандо, назовем его вариант В. Этот денежный поток можно изобразить на шкале времени таким образом:
Как видно из рисунка, платежи по 25,000 делаются в начале каждого годового периода. Например, вы решили класть на счет в банке по 25,000 каждый год 1 января. Первый платеж принесет нам проценты за 5 лет, второй — за 4 года, третий — за 3 года, четвертый — за 2 год и, наконец, платеж, сделанный в начале пятого года, принесет нам проценты за один год. Коэффициенты наращения я взяла из соответствующей таблицы, которую можно открыть по ссылке.
25,000*1,6105 25,000*1,4641 25,000*1,3310 25,000*1,2100 25,000*1,1000 = 25,000* (1,6105 1,4641 1,3310 1,2100 1,1000) = 25,000*6,7156 = 167,890
Таким образом, если начинать вносить 25,000 каждый год в начале годового периода и делать это в течение 5 лет, то через 5 лет сумма на счете будет равна $167,890. Этот вариант В выгодней, чем варианты А и Б, которые были рассмотрены раньше.
- Вариант А — $100,000, внесенные сегодня, накопят на банковском счете через 5 лет только 161,050
- Вариант Б — $25,000, внесенные на счет в конце каждого из 5 последующих лет, накопят через 5 лет только $152,628
Как видно из двух последних примеров, большое значение имеет момент, когда производятся платежи: в начале или в конце периода. Поэтому, если нужно рассчитать дисконтированную или будущую стоимость любых денежных потоков, желательно рисовать шкалу времени, на которой отметить суммы и коэффициенты, соответствующие каждому периоду.
Как эти расчеты могут пригодиться в жизни?
В примерах выше были разобраны абстрактные примеры аннуитетов. Но с аннуитетными денежными потоками мы встречаемся и в реальной жизни. Например, интересно будет рассчитать, сколько удастся накопить на сберегательном счете, если откладывать каждый месяц часть зарплаты.
Подобным же образом можно будет рассчитать, скажем, дисконтированную стоимость всех платежей по автокредиту. Выплаты банку при покупке автомобиля (и не только автомобиля) в кредит представляют собой аннуитет. Его дисконтированная (приведенная к сегодняшнему дню) стоимость — это и будет стоимость приобретаемого автомобиля.
Можно точно узнать, сколько вы переплачиваете при покупке машины в кредит в сравнении с вариантом покупки с уплатой полной суммы сразу. А также можно будет сравнить кредитные предложения разных банков. Единственная проблема в таких расчетах – выбрать правильную месячную ставку дисконтирования.
Способ определения величины показателя
Рассмотрим подробнее, как рассчитать коэффициент дисконтирования. Обычно речь идет о многошаговом расчете перспективности и экономической эффективности инвестиционного начинания, поэтому фактор дисконтирования приводит объем потока на n-м шаге к моменту приведения.
Общая формула дисконтирования потока денег имеет такой вид:
PV = FV * 1/(1 R)n
- PV – приведенная стоимость;
- FV – будущая стоимость.
В этой формуле выделяется компонент, определяющий величину фактора приведения. Собственно, формула расчета коэффициента дисконтирования выглядит так:
КД = 1/(1 R)n
- R – установленное значение нормы дисконта;
- n – количество периодов (шагов), представляющее собой число лет (месяцев) от будущего до текущего момента.
Получившийся показатель всегда имеет значение меньше единицы. Он показывает стоимость одной инвестированной денежной единицы (рубля, евро, доллара) через определенное время при соответствии условий тем, которые приняты для вычисления.
Важнейшей составной частью для расчета коэффициента является ставка дисконтирования, которую еще называют нормой дисконта. Для ее определений существует целый ряд методик, основанных на различных принципах:
- дивидендный метод (модель Гордона);
- стоимость капитальных активов предприятия (модель CAPM и ее многочисленные модификации);
- наличие заемных и собственных средств (модель WACC);
- метод значений рентабельности капитала (ROE, ROA, ROACE, ROCE);
- метод вычисления рисковых премий (кумулятивный);
- экспертный метод, основанный на субъективных прогнозах специалистов.
За норму дисконта можно принимать темпы инфляционных процессов, стоимость долгосрочных депозитов или кредитов, размер ставки рефинансирования Центробанка и т.д. В любом случае, каков будет этот критерий, решает на свой страх и риск инвестор. Если норма дисконта установлена неверно или в ней не учтены все основные риски, то и фактор приведения будет некорректным.
Это даст инвестору неверный прогноз, который может привести к убыткам. Другая составляющая формулы – это жизненный цикл начинания, то есть количество рассматриваемых периодов, в течение которых проект будет генерировать денежные потоки. Чем точнее, установлены эти две вводные, тем более точным будет конечный результат.







