Конвертация валюты и начисление процентов
Рассмотрим совмещение конвертации (обмена) валюты и наращение простых процентов, сравним результаты от непосредственного размещения имеющихся денежных средств в депозиты или после предварительного обмена на другую валюту. Всего возможно 4 варианта наращения процентов:
- Без конвертации. Валютные средства размещаются в качестве валютного депозита, наращение первоначальной суммы производится по валютной ставке путем прямого применения формулы простых процентов.
- С конвертацией. Исходные валютные средства конвертируются в рубли, наращение идет по рублевой ставке, в конце операции рублевая сумма конвертируется обратно в исходную валюту.
- Без конвертации. Рублевая сумма размещается в виде рублевого депозита, на который начисляются проценты по рублевой ставке по формуле простых процентов.
- С конвертацией. Рублевая сумма конвертируется в какую-либо конкретную валюту, которая инвестируется в валютный депозит. Проценты начисляются по валютной ставке. Наращенная сумма в конце операции обратно конвертируется в рубли.
Операции без конвертации не представляют сложности. В операции наращения с двойной конвертацией имеются два источника дохода: начисление процента и изменение курса.
Причем начисление процента является безусловным источником (ставка фиксирована, инфляцию пока не рассматриваем). Изменение же обменного курса может быть как в ту, так и в другую сторону, и оно может быть как источником дополнительного дохода, так и приводить к потерям. Далее мы конкретно остановимся на двух вариантах (2 и 4), предусматривающих двойную конвертацию.
Предварительно введем следующие ОБОЗНАЧЕНИЯ:

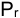
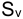
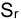
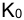
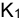
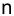
i — ставка наращения для рублевых сумм (в виде десятичной дроби);
j — ставка наращения для конкретной валюты.
ВАРИАНТ: 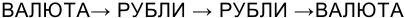
Операция состоит из трех этапов: обмена валюты на рубли, наращения рублевой суммы, обратное конвертирование рублевой суммы в исходную валюту. Наращенная сумма, получаемая в конце операции в валюте, составит
Как видим, три этапа операции нашли свое отражение в этой формуле в виде трех сомножителей.
Множитель наращения с учетом двойной конвертации равен
где 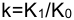
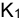
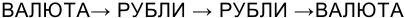
Простая годовая ставка процентов, характеризующая доходность операции в целом,равна
Подставим в эту формулу записанное ранее выражение для 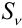
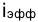
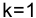
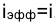
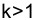 , доходность (эффективность) операции оказывается равной нулю. Из равенства
, доходность (эффективность) операции оказывается равной нулю. Из равенства 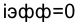
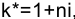
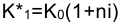
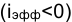
Теперь определим максимально допустимое значение курса обмена в конце операции К1, при котором эффективность будет равна существующей ставке по депозитам в валюте, и применение двойной конвертации не дает никакой дополнительной выгоды. Для этого приравняем множители наращения для двух альтернативных операций
Из записанного равенства следует, что
ВЫВОД 2: Депозит валюты через конвертацию в рубли выгоднее валютного депозита, если обменный курс в конце операции ожидается меньше max 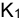
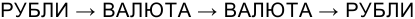
Рассмотрим теперь вариант с двойной конвертацией, когда имеется исходная сумма в рублях. В этом случае трем этапам операции соответствуют три сомножителя следующего выражения для наращенной суммы
Здесь также множитель наращения линейно зависит от ставки, но теперь от валютной ставки процентов. От конечного курса обмена он также зависит линейно.
Проведем теоретический анализ эффективности этой операции с двойной конвертацией и определим критические точки.
Доходность операции в целом определяется по формуле
Отсюда, подставив выражение для 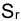
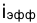
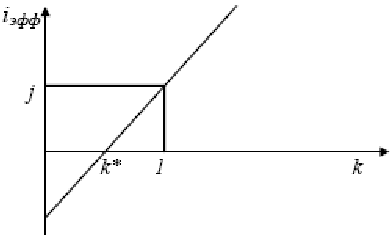
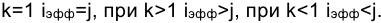
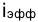
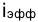
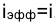
Откуда
ВЫВОД 4: Депозит рублевых сумм через конвертацию в валюту выгоднее рублевого депозита, если обменный курс в конце операции ожидается больше min 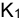
Теперь рассмотрим совмещение конвертации валюты и наращение сложных процентов. Ограничимся одним вариантом.
ВАРИАНТ: 
Три этапа операции записываются в одной формуле для наращенной суммы
где i — ставка сложных процентов.
Множитель наращения
где 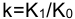
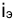
Из формулы наращения по сложным процентам
следует, что
Подставив в эту формулу значение 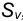
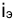
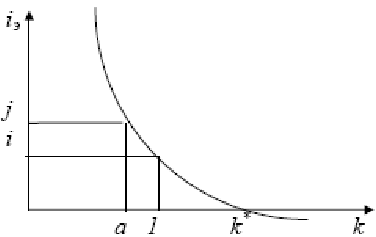
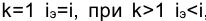
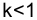
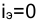
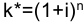
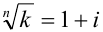
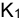
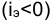
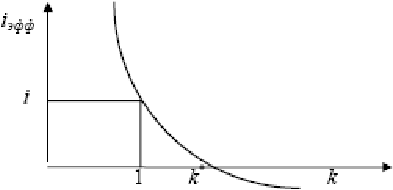
Максимально допустимое значение k, при котором доходность операции будет равна доходности при прямом инвестировании валютных средств по ставке j (т. а на рис. 4), находится из равенства соответствующих множителей наращения
откуда
ВЫВОД 6: Депозит валюты через конвертацию в рубли выгоднее валютного депозита, если обменный курс в конце операции ожидается меньше max 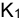
Возможно эта страница вам будет полезна:
Непрерывные проценты: наращение, дисконтирование, связь дискретных и непрерывных процентных ставок.
Для непрерывных процентов не существует различий между процентной и учетной ставками, поскольку сила роста – универсальный показатель. Однако наряду с постоянной силой роста может использоваться переменная процентная ставка, величина которой меняется по заданному закону (математической функции).
Непрерывное начисление процентов используется при анализе сложных финансовых задач, например, обоснование и выбор инвестиционных решений. Оценивая работу финансового учреждения, где платежи за период поступают многократно, целесообразно предполагать, что наращенная сумма непрерывно меняется во времени и применять непрерывное начисление процентов.
Все ситуации, которые мы до сих пор рассматривали, относились к дискретным процентам, поскольку их начисление осуществляется за фиксированные промежутки времени (год, квартал, месяц, день, час). Но на практике нередко встречаются случаи, когда проценты начисляются непрерывно, за сколь угодно малый промежуток времени. Если бы проценты начислялись ежедневно, то годовой коэффициент (множитель) наращения выглядел так:
kн = (1 j / m)m = (1 j / 365)365
Но поскольку проценты начисляются непрерывно, то m стремится к бесконечности, а коэффициент (множитель) наращения стремится к e j:
где e ≈ 2,718281, называется числом Эйлера и является одной из важнейших постоянных математического анализа.
Отсюда можно записать формулу наращенной суммы для n лет:
FV = PV • e j • n = P • eδ • n
Ставку непрерывных процентов называют силой роста (force of interest) и обозначают символом δ, в отличие от ставки дискретных процентов ( j ).
Пример. Кредит в размере на 100 тыс. долларов получен сроком на 3 года под 8% годовых. Определить сумму подлежащего возврату в конце срока кредита, если проценты будут начисляться:
а) один раз в год;
б) ежедневно;
в) непрерывно.
Решение:
Используем формулы дискретных и непрерывных процентов:
начисление один раз в год
FV = 100’000 • (1 0,08)3 = 125’971,2 долларов;
ежедневное начисление процентов
FV = 100’000 • (1 0,08 / 365)365 • 3 = 127’121,6 долларов
непрерывное начисление процентов
FV = 100’000 • e0,08 • 3 = 127’124,9 долларов.
12. Расчет срока кредита:
– при наращении по сложной годовой ставке %,
– при наращении по номинальной ставке % m раз в году,
– при наращении по постоянной силе роста.
В любой простейшей финансовой операции всегда присутствуют четыре величины: современная величина (PV), наращенная или будущая величина (FV), процентная ставка (i) и время (n).
Иногда при разработке условий финансовой сделки или ее анализе возникает необходимость решения задач, связанных с определением отсутствующих параметров, таких как срок финансовой операции или уровень процентной ставки.
Как правило, в финансовых контрактах обязательно фиксируются сроки, даты, периоды начисления процентов, поскольку фактор времени в финансово-коммерческих расчетах играет важную роль. Однако бывают ситуации, когда срок финансовой операции прямо в условиях финансовой сделки не оговорен, или когда данный параметр определяется при разработке условий финансовой операции.
Обычно срок финансовой операции определяют в тех случаях, когда известна процентная ставка и величина процентов.
Если срок определяется в годах, то
n = (FV – PV) : (PV • i),
а если срок сделки необходимо определить в днях, то появляется временная база в качестве сомножителя:
t = [(FV – PV) : (PV • i)] • T.
Так же как для простых процентов, для сложных процентов необходимо иметь формулы, позволяющие определить недостающие параметры финансовой операции:
n = [log (FV / PV)] / [log (1 i)] = [log (FV / PV) ] / [log(1 j / m)m];
- ставка сложных процентов:
Пример. Что выгоднее: увеличение вклада в три раза за три года или 46% годовых?
Решение:
Такого рода задачи приходится решать не только лицам, занимающимся финансовой работой, но и населению, когда решается вопрос о том, куда выгоднее вложить деньги. В таких случаях решение сводится к определению процентной ставки:
Таким образом, увеличение вклада за три года в три раза эквивалентно годовой процентной ставке в 44,3%, поэтому размещение денег под 46% годовых будет более выгодно.
13. Расчет срока кредита:
– при дисконтировании по сложной годовой учетной ставке,
– при дисконтировании по номинальной учетной ставке m раз в году.
14. Расчет процентной ставки:
– при наращении по сложной годовой ставке %,
– при наращении по номинальной ставке % m раз в году,
– при наращении по постоянной силе роста.
15. Расчет процентной ставки:
– при дисконтировании по сложной годовой учетной ставке,
– при дисконтировании по номинальной учетной ставке m раз в году.
§
В финансовой литературе ряд распределенных во времени выплат и поступлений называется потоком платежей.
Потоки платежей являются неотъемлемой частью всевозможных финансовых операций: с ценными бумагами, в управлении финансами предприятий, при осуществлении инвестиционных проектов, в кредитных операциях, при оценке бизнеса, при оценке недвижимости, выборе альтернативных вариантов финансовых операций и т. п.
Члены потока могут быть как положительными величинами (поступления), так и отрицательными величинами (выплатами), а временные интервалы между членами такого потока могут быть равными и неравными.
Поток платежей, все члены которого имеют одинаковое направление (знак), а временные интервалы между последовательными платежами постоянны, называется финансовой рентой или аннуитетом.
При рассмотрении финансовой ренты используются основные категории:
- член ренты (R) – величина каждого отдельного платежа;
- период ренты (t) – временной интервал между членами ренты;
- срок ренты (n) – время от начала финансовой ренты до конца последнего ее периода;
- процентная ставка (i) – ставка, используемая при наращении платежей, из которых состоит рента.
Поскольку условия финансовых сделок весьма разнообразны, постольку разнообразны и виды потоков платежей. В основе классификации финансовых рент положены различные качественные признаки:
- В зависимости от периода продолжительности ренты выделяют
- годовую ренту, которые представляют собой ежегодные платежи, т.е. период ренты равен 1 году;
- срочную ренту, при которой период ренты может быть как более, так и менее года.
- По числу начислений процентов различают
- ренты с начислением 1 раз в год;
- ренты с начислением mраз в год;
- непрерывное начисление.
- По величине членов ренты могут быть
- постоянные ренты, где величина каждого отдельного платежа постоянна, т.е. рента с равными членами;
- переменные ренты, где величина платежа варьирует, т.е. рента с неравными членами.
- По числу членов ренты они бывают
- с конечным числом членов (ограниченные ренты), когда число членов ренты конечно и заранее известно;
- с бесконечным числом (вечные ренты), когда число ее членов заранее не известно.
- По вероятности выплаты ренты делятся на
- верные ренты, которые подлежат безусловной выплате, т.е. не зависят не от каких условий, например, погашение кредита;
- условные ренты, которые зависят от наступления некоторого случайного события.
- По методу выплаты платежей выделяют
- обычные ренты, которые на практике встречаются чаще всего, – с выплатой платежа в конце периода ренты (постнумерандо);
- ренты, с выплатой в начале периода ренты (пренумерандо).
Под потоком платежей понимается некоторая последовательность платежей во времени (Cash Flow).
Потоки могут быть:
§ Регулярные;
§ Нерегулярные.
Элементами нерегулярного потока являются как положительные поступления, так и отрицательные выплаты, а соответствующие платежи могут производиться через различные интервалы времени.
Финансовая рента (аннуитет) – поток одинаковых платежей, все элементы которых положительные величины, а временные интервалы между платежами – одинаковы.
Характеристики ренты:
§ Размер платежа (Payment – PMT);
§ Период ренты;
§ Срок ренты;
§ Процентная ставка.

По моменту выплаты в пределах периода между платежами ренты делятся:
a) Постнумерандо – выплаты в конце периода;
b) Пренумерандо – выплаты в начале периода;
c) В середине периода.
21. Расчет наращенной суммы постоянной годовой ренты ПОСТНУМЕРАНДО при начислении % один раз в год.
Получатели поступлений оценивают свой доход суммарной величиной за полный срок действия платежа, разумеется, с учетом временной неравноценности денег.
Наращенная сумма – сумма всех платежей с начисленными на них процентами к концу срока ренты. Это может быть обобщенная сумма задолженности, итоговый объем инвестиций и т.п.
Наращенные отдельные платежи представляют собой члены геометрической прогрессии с первым членом равным R и множителем равным (1 i).
Рассмотрим определение наращенной суммы на примере наиболее простого случая, – годовой постоянной обычной ренты:
где FVA – наращенная сумма ренты;
R – размер члена ренты, т.е. размер очередного платежа;
i – годовая процентная ставка, по которой на платежи начисляются сложные проценты;
n – срок ренты в годах,
s n;i – коэффициент наращения ренты.
Пример. На счет в банке в течении пяти лет в конце каждого года будут вноситься суммы в размере 500 руб., на которые будут начисляться проценты по ставке 30%. Определить сумму процентов, которую банк выплатит владельцу счета.
Решение:
Поскольку период ренты равен одному году, то это годовая рента; проценты начисляются один раз в год; взносы будут в конце периода ренты, постнумерандо, значит это обычная рента; сумма платежа постоянна на протяжении всего срока ренты, что характерно для постоянной ренты; число членов ренты пять, т.е. конечно, следовательно, ограниченная рента; а выплаты носят безусловный характер, таким образом, это верная рента.
Сумма всех взносов с начисленными процентами будет равна:
Расчет современной стоимости постоянной годовой ренты ПОСТНУМЕРАНДО при начислении % один раз в год.
Помимо наращенной суммы обобщающей характеристикой потока платежей является современная величина. Современная (текущая) величина потока платежей (капитализированная или приведенная величина) – это сумма платежей, дисконтированных на момент начала ренты по ставке начисляемых сложных процентов. Это важнейшая характеристика финансового анализа, т.к. является основой для измерения эффективности различных финансово-кредитных операций, сравнения условий контрактов и т.п. Данная характеристика показывает, какую сумму следовало бы иметь первоначально, чтобы, разбив ее на равные взносы, на которые начислялись бы установленные проценты в течение всего срока, можно было бы получить указанную наращенную сумму.
В этом случае реализуется схема дисконтирования: все элементы с помощью дисконтных множителей приведены к одному моменту времени, что позволяет их суммировать.
В простейшем случае, для годовой обычной ренты с выплатами в конце каждого года, когда момент оценки совпадает с началом ренты, современная величина финансовой ренты равна:
Дробь в формуле – коэффициент приведения ренты (an;i), значения которого табулированы для широкого круга значений, поскольку зависят от ставки процентов (i) и от числа лет (n) (Приложение 5).
Пример. Определить по данным примера современную величину ренты.
Решение:
Современная величина ренты составит:
Таким образом, все производимые в будущем платежи оцениваются в настоящий момент в размере 1’217,78 руб.
22. Расчет наращенной суммы постоянной p-срочной ренты ПОСТНУМЕРАНДО при начислении % m раз в год (p=m).
Бывают случаи, когда рентные платежи вносятся несколько раз в год равными суммами (срочная рента), а начисление процентов производится только раз в году. Тогда наращенная величина ренты будет определяться по формуле:
Также нередки случаи, когда рентные платежи вносятся несколько раз в году и начисление процентов также происходит несколько раз в год, но число рентных платежей не равно числу периодов начисления процентов, т.е. p ≠ m. Тогда формула по которой можно определить наращенную величину финансовой ренты примет вид:
На практике большее распространение получил поток постнумерандо, поскольку согласно общим принципам учета принято подводить итоги и оценивать финансовый результат операции или иного действия по окончании очередного отчетного периода. Что же касается поступления денежных средств в счет оплаты, то на практике они чаще всего распределены во времени неравномерно и поэтому для удобства все поступления относят к концу периода, что позволяет использовать формализованные алгоритмы оценки.
Поток пренумерандо имеет значение при анализе различных схем накопления денежных средств для последующего их инвестирования.
Рента пренумерандо отличается от обычной ренты числом периодов начисления процентов. Поэтому наращенная сумма ренты пренумерандо будет больше наращенной суммы обычной ренты в (1 i) раз.
Для годовой ренты пренумерандо с начислением процентом один раз в год формула примет вид:
Для годовой ренты пренумерандо с начислением процентов несколько раз в год:
Расчет современной стоимости постоянной p-срочной ренты ПОСТНУМЕРАНДО при начислении % m раз в год (p=m).
Рассмотрим расчет современной величины ренты для различных ее видов:
- годовая рента с начислением процентов несколько раз в год:
- срочная рента при начислении процентов один раз в год:
- срочная рента с неоднократным начислением процентов в течение года, при условии, что число выплат не равно числе начислений, т.е. p ≠ m :
23. Определение размера очередного платежа постоянной финансовой ренты ПОСТНУМЕРАНДО (p=m=1).
Последовательные платежи в виде постоянной обычной годовой ренты определяются основными параметрами:
R – размер платежа;
n – срок ренты в годах;
i – годовая ставка процентов.
Однако при разработке условий финансовой операции могут возникать ситуации, когда заданной величиной является одна из двух обобщающих характеристик и неполный набор параметров ренты. В таких случаях находят недостающий параметр.
При определении члена ренты возможны два варианта, зависящие от того, какая величина является исходной:
а) наращенная сумма. Если сумма долга определена на какой-либо момент в будущем (FVA), тогда величину последующих взносов в течение n лет при начислении на них процентов по ставке i можно определить по формуле:
Пример. Для покупки автомобиля через 5 лет потребуется 50 тыс. руб. Определите размер ежегодных взносов, вносимых в конце каждого года в банк, который начисляет проценты по ставке 40%.
Решение:
В данном случае известна наращенная величина постоянной финансовой ренты, поэтому размер ежегодных взносов будет равен:
Таким образом, чтобы накопить на счете необходимую сумму для покупки автомобиля следует в конце каждого года в течении пяти лет откладывать 4’568 руб.
б) современная величина финансовой ренты, тогда, исходя из ставки процента и срока ренты, разовый платеж находится по формуле:
Пример. Сумма 10 тыс. долларов предоставлена в долг на 5 лет под 8% годовых. Определить ежегодную сумму погашения долга.
Решение:
Известна современная величина долга, отсюда:
Таким образом, ежегодно необходимо будет возвращать сумму 2’504,56 руб.
Можно произвести проверку: сумма долга с начисленными на нее процентами к концу пятого года будет составлять:
FV = 10’000 • (1 0,08)5 = 14’693,28 руб.
Наращенная сумма для потока платежей размером 2’504,56 руб. составит:
Следовательно, величина члена финансовой ренты определена верно. Незначительное расхождение вызвано округлением расчетов.
Современная величина ренты пренумерандо рассчитывается путем умножения современной величины обычной ренты на соответствующий множитель наращения.
24. Определение срока ссуды постоянной финансовой ренты ПОСТНУМЕРАНДО (p=m=1).
§
В финансовой математике широко представлены все виды статистических показателей: абсолютные, относительные и средние величины.
Процентные деньги или просто проценты в финансовых расчетах представляют собой абсолютную величину дохода (приращение денег) от предоставления денег в долг в любой его форме (причем эта финансовая операция может реально и не состояться): 1>>>
- выдача денежной ссуды;
- продажа в кредит;
- сдача в аренду;
- депозитный счет;
- учет векселя;
- покупка облигаций и т.п.
Таким образом, проценты можно рассматривать как абсолютную “цену долга”, которую уплачивают за пользование денежными средствами.
Абсолютные показатели чаще всего не подходят для сравнения и оценки ввиду их несопоставимости в пространстве и во времени. Поэтому в финансово-коммерческих расчетах широко пользуются относительными показателями.
Относительный показатель, характеризующий интенсивность начисления процентов за единицу времени, – процентная ставка. Методика расчета проста: отношение суммы процентных денег, выплачивающихся за определенный период времени, к величине ссуды. Этот показатель выражается либо в долях единицы, либо в процентах. Таким образом, процентная ставка показывает, сколько денежных единиц должен заплатить заемщик за пользование в течение определенного периода времени 100 единицами первоначальной суммы долга.
Начисление процентов, как правило, производится дискретно, т.е. за фиксированные одинаковые интервалы времени, которые носят название “период начисления“, – это отрезок времени между двумя следующими друг за другом процедурами взимания процентов. Обычные или декурсивные (postnumerando) проценты начисляются в конце периода. В качестве единицы периода времени в финансовых расчетах принят год, однако это не исключает использования периода менее года: полугодие, квартал, месяц, день, час.
Период времени от начала финансовой операции до ее окончании называется сроком финансовой операции.
Для рассмотрения формул, используемых в финансовой математике, необходимо ввести ряд условных обозначений:
I – проценты за весь срок ссуды (interest);
PV – первоначальная сумма долга или современная (текущая) стоимость (present value);
i – ставка процентов за период (interest rate);
FV – наращенная сумма или будущая стоимость (future value), т.е. первоначальная сумма долга с начисленными на нее процентами к концу срока ссуды;
n – срок ссуды в годах.
После начисления процентов возможно два пути:
- либо их сразу выплачивать, по мере их начисления,
- либо отдать потом, вместе с основной суммой долга.
Увеличение суммы долга в связи с присоединением к ней процентных денег называется наращением, а увеличенная сумма – наращенной суммой. Отсюда можно выделить еще один относительный показатель, который называется коэффициент наращения или множитель наращения, – это отношение наращенной суммы к первоначальной сумме долга. Коэффициент наращения показывает, во сколько раз наращенная сумма больше первоначальной суммы долга, т.е. по существу является базисным темпом роста.
Основу коммерческих вычислений составляют ссудо-заемные операции, в которых проявляется ярче всего необходимость учета временной ценности денег. Несмотря на то, что в основе таких расчетов заложены простейшие на первый взгляд схемы начисления процентов, эти расчеты многообразны ввиду многообразия условий финансовых контрактов в отношении частоты и способов начисления процентов, а также вариантов предоставления и погашения ссуд.
Существуют различные способы начисления процентов и соответствующие им виды процентных ставок.
Российская экономика все более интегрируется в мировую экономику, что требует использования финансового инструментария, применяемого развитыми странами и международными организациями в финансовой практике.
Становление рыночных отношений в России сопровождается появлением навыков и методов, которыми приходится овладевать для оценки инвестиционных проектов, в операциях на рынке ценных бумаг, в ссудо-заемных операциях, в оценке бизнеса и др.
Кардинальное изменение банковской системы, внедрение новых форм собственности, развитие фондового рынка и финансовой самостоятельности предприятий сделали актуальным управление финансовыми ресурсами, одним из краеугольных элементов которого являются финансовые вычисления, базирующиеся на понятии временной ценности денег.
Известный всем лозунг “время – деньги” имеет под собой реальную основу, позволяющую определить истинную ценность денег с позиции текущего момента.
Важность учета фактора времени обусловлена принципом неравноценности денег, относящихся к различным моментам времени: равные по абсолютной величине денежные суммы “сегодня” и “завтра” оцениваются по разному, – сегодняшние деньги ценнее будущих
Существуют два подхода и соответствующие им два типа экономического мышления:
- статический подход не учитывает фактор времени, – в соответствии с этим, здесь возможно оперирование денежными показателями, относящимися к различным периодам времени, и их суммирование;
- динамический подход используется в финансовом анализе и финансовом менеджменте, где фактор времени играет решающую роль и его необходимо обязательно учитывать, поэтому здесь неправомерно суммировать денежные величины, относящиеся к различным моментам времени.
Эти два подхода соответствуют “бухгалтерскому” и “экономическому” принципам анализа затрат. Именно динамический подход предполагает включение в расходы так называемых неявных затрат, определяемых на основе принципа альтернативной ценности.
В условиях централизованно планируемой экономики на внутреннем уровне господствовал первый тип экономического мышления. Почему?
- Во-первых, ни юридические, ни физические лица, как правило, не располагали крупными суммами временно свободных денежных средств, поскольку для юридических лиц ресурсы жестко лимитировались, а для физических лиц заработать крупные суммы денег было невозможно.
- Во-вторых, единственный путь использования временно свободных денежных средств был связан с размещением их в Сбербанке.
Переход к рыночной экономике изменил ситуацию и тип экономического мышления, поскольку деньги приобретают для широкого круга людей объективно существующую временную ценность. Сегодня можно заработать любую сумму денег, поскольку нет жестких ограничений ни для физических, ни для юридических лиц. Заработанные деньги можно пустить на потребление или инвестировать в экономику, поскольку ликвидируется монополия государства на пользование сбережениями населения. Финансовые и коммерческие расчеты стали постоянно сопровождать любого человека, будь то предприниматель или пенсионер.
Если процентные деньги не выплачиваются сразу по мере их начисления, а присоединяются к первоначальной сумме долга, то долг, таким образом, увеличивается на невыплаченную сумму процентов, и последующее начисление процентов происходит на увеличенную сумму долга:
FV = PV I = PV PV • i = PV • (1 i)
– за один период начисления;
FV = (PV I) • (1 i) = PV • (1 i) • (1 i) = PV • (1 i)2
– за два периода начисления;
отсюда, за n периодов начисления формула примет вид:
FV = PV • (1 i)n = PV • kн,
где FV – наращенная сумма долга;
PV – первоначальная сумма долга;
i – ставка процентов в периоде начисления;
n – количество периодов начисления;
kн – коэффициент (множитель) наращения сложных процентов.
Эта формула называется формулой сложных процентов.
Как было выше указано, различие начисления простых и сложных процентов в базе их начисления. Если простые проценты начисляются все время на одну и ту же первоначальную сумму долга, т.е. база начисления является постоянной величиной, то сложные проценты начисляются на увеличивающуюся с каждым периодом начисления базу. Таким образом, простые проценты по своей сути являются абсолютными приростами, а формула простых процентов аналогична формуле определения уровня развития изучаемого явления с постоянными абсолютными приростами. Сложные проценты характеризуют процесс роста первоначальной суммы со стабильными темпами роста, при наращении ее по абсолютной величине с ускорением, следовательно, формулу сложных процентов можно рассматривать как определение уровня на базе стабильных темпов роста.
Пример №15
В течение 3 лет на расчетный счет в конце каждого года поступает по 10 млн. руб., на которые начисляются проценты по сложной годовой ставке 10%. Требуется определить сумму на расчетном счете к концу указанного срока.
Решение:
Годовая рента, начисление процентов m раз в году.
Посмотрим как усложнится формула, если предположить теперь, что платежи делают один раз в конце года, а проценты начисляют m раз в году. Это означает, что применяется каждый раз ставка j/m, где j — номинальная ставка процентов. Тогда члены ренты с начисленными до конца срока процентами имеют вид
Если прочитать предыдущую строку справа налево, то нетрудно увидеть, что перед нами опять геометрическая прогрессия, первым членом которой является R, знаменателем 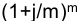
Сумма членов этой прогрессии и будет наращенной суммой ренты. Она равна
Рента р-срочная, m=1
Найдем наращенную сумму при условии, что рента выплачивается р раз в году равными платежами, а проценты начисляются один раз в конце года. Если R — годовая сумма платежей, то размер отдельного платежа равен R/p. Тогда последовательность платежей с начисленными до конца срока процентами также представляет собой геометрическую прогрессию, записанную в обратном порядке,
у которой первый член R/p, знаменатель 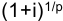
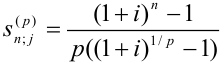
р-срочной ренты при m=1.
Рента р-срочная, р=m
В контрактах часто начисление процентов и поступление платежа совпадают во времени. Таким образом число платежей р в году и число начислений процентов m совпадают, т.е. р=т. Тогда для получения формулы расчета наращенной суммы можно воспользоваться аналогией с годовой рентой и одноразовым начислением процентов в конце года, для которой
Различие будет лишь в том, что все параметры теперь характеризуют ставку и платеж за период, а не за год.
Таким образом получаем
Рента р-срочная, 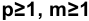
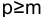
Первый член ренты R/p, уплаченный спустя 1/р года после начала, составит к концу срока вместе с начисленными на него процентами
Второй член ренты к концу срока возрастет до
и т.д. Последний член этой записанной в обратном порядке геометрической прогрессии равен R/p, ее знаменатель 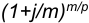
В результате получаем наращенную сумму
Отметим, что из нее легко получить все рассмотренные выше частные случаи, задавая соответствующие значения р и т.
Пример №1
Определим проценты и сумму накопленного долга, если ссуда равна 100000 руб., срок долга 1,5 года при ставке простых процентов, равной 15% годовых.
Решение:
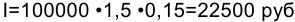
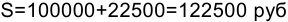
Процентная ставка i — относительная величина, измеряемая в десятичных дробях или %, она определяется делением процентов на первоначальную сумму:
На рис. 1.1. представлен график роста по простым процентам.
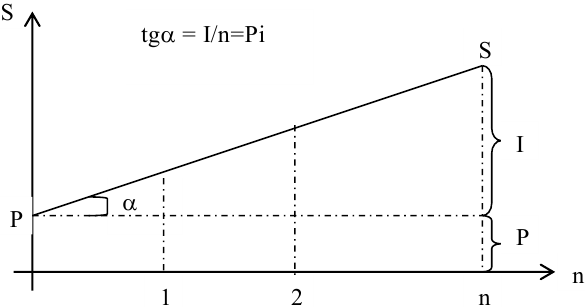
Практика начисления простых процентов
При анализе краткосрочных операций (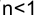
где t — срок контракта в днях;
К — временная база, число дней в году.
Здесь возможно несколько вариантов расчета процентов, различающихся выбором временной базы К и способом измерения срока пользования ссудой.
Часто за базу измерения времени берут год, условно состоящий из 360 дней (12 месяцев по 30 дней в каждом).
Если К= 365 (366), то получают точный процент, если K=12*30=360, получают обыкновенный процент.
Определение числа дней пользования ссудой также может быть точным, либо приближенно. В первом случае вычисляют фактическое число дней между двумя датами, во втором -продолжительность ссуды определяется числом месяцев и дней ссуды, приближенно считая все месяцы равными, содержащими по 30 дней. В обоих случаях счет дней 12 начинается со следующего дня после открытия операции.
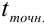
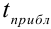
Комбинируя различные варианты временной базы и методов подсчета дней ссуды, получаем три варианта расчета процентов, применяемые в практике (цифры в скобках обозначают соответственно величину t и К):
1) (365/365) — точные проценты с точным числом дней. Британский метод. Используют в России, США, Великобритании;
2) (365/360) обыкновенные проценты с точной длительностью операции — французский метод;
3) (360/360) обыкновенные проценты с приближенной длительностью операции — германский метод .





