- § 9.1. дисконтирование: задача 1. дисконтирование потока дохода инвестор предоставил кредит
- 1.1Простые ставки
- 1.2Сложные ставки
- 2.1Учет по простой учетной ставке
- 2.2Учет по сложной учетной ставке
- Дисконтированный – сборник задач-экономика – методические рекомендации по решению задач по соответствующим темам…
- Задача – срок окупаемости проекта простым способом и с учетом дисконтирования | инфо экономика
- Задачи с решениями по финансовой математике
- Решение:
§ 9.1. дисконтирование: задача 1. дисконтирование потока дохода инвестор предоставил кредит
Задача 1. Дисконтирование потока дохода
Инвестор предоставил кредит размером 10000 долларов на 5 лет. В конце каждого года он получает 900 долларов, а по истечении 5 лет ссуда будет полностью возвращена.
Для подобных кредитов на рынке установилась ставка дохода (дисконта) в 11% годовых.
Какова чистая текущая стоимость (ЧТС) подобного инвестирования денег?
Таблица шести функций денег.
Ставка дисконта 11% (начисление процентов ежегодно)

Решение. С использованием таблиц шести функций денег (колонка текущей стоимости аннуитета) текущая стоимость ежегодного (в течение пяти лет) дохода в 900 долларов при ставке 11% составляет:
900 X 3,69590 = 3326,31 доллара.
Текущая стоимость платежа в 10000 долларов, ожидаемого к получению через 5 лет, при ставке 11% (колонка текущей стоимости единицы) составляет:
10000 X 0,59345 = 5934,51 доллара.
Текущая стоимость инвестиционных средств равняется сумме текущей стоимости потока ежегодных поступлений (3326,31 доллара) и текущей стоимости реверсии (5934,51 доллара):
3326,31 5934,51 «= 9260,82 доллара.
Эти величины могут быть также получены с использованием финансового калькулятора или персонального компьютера.
Описанная процедура иллюстрирует базовый алгоритм расчетов в методе дисконтирования. Во многих ситуациях, когда величина прогнозируемого рентного дохода меняется от периода к периоду, может потребоваться дополнительная процедура.
Задача 2. Дисконтирование потока дохода и реверсии
Инвестор приобретает недвижимость за 275000 долларов и сдает ее в аренду на 10 лет с получением следующих абсолютных сумм чистого рентного дохода, выплачиваемых авансом.
Ожидается, что к концу срока аренды недвижимость будет стоить порядка 300000 долларов.
Какова текущая стоимость данного недвижимого имущества, если рыночная ставка дисконта для данного типа недвижимости 11%?
Текущая стоимость рентных платежей
| г» | Годовая арендная плата, долларов | Текущая стойкость единицы при 11%, долларов | Текущая стоимость, долларов |
| 0 | 30000 | 1,000000 | 30000,00 |
| 1 | 31000 | 0,900901 | 27927.93 |
| 2 | 32000 | 0,811622 | 25971,92 |
| 3 | 33000 | 0,731191 | 24129,32 |
| 4 | 34000 | 0,658731 | 22396.85 |
| 5 | 35000 | 0,593451 | 20770,80 |
| 6 | 36000 | 19247,07 | |
| 7 | 37000 | 0,481658 | 17821,36 |
| 8 | 38000 | 0.433926 | 16489.21 |
| 9 | 39000 | 0.390925 | 15246,07 |
| Чистая текущая стоимость рентного потока | 220000,53 1 | ||
Чистая текущая стоимость реверсии (платежа в 300000 долларов, ожидаемого к получению через 10 лет при ставке 11%) составляет:
0, 352184 X 300000 = 105655,20 доллара.
Чистая текущая стоимость недвижимости составляет: 220000,53 #9830; 105655,20 = 325655,73 доллара.
Задача 2 базировалась на абсолютно чистой ренте. Часто арендодатель несет ответственность за оплату части расходов по содержанию недвижимости. Эти расходы вычитаются из арендной платы, и полученный результат дисконтируется в текущую стоимость. Следующий пример показывает, как вычислять текущую стоимость потока дохода и текущую стоимость реверсии в том случае, если операционные расходы оплачиваются владельцем из рентных платежей, а расходы по продаже вычитаются из поступлений от продажи недвижимости в конце срока владения.
Задача 3 иллюстрирует типичный набор информации, доступной оценщику для определения стоимости недвижимости с использованием метода дисконтирования денежных потоков (ДДП).
Задача 3. Использование дисконтирования для оценки вариантов инвестирования
Инвестору сделали предложение приобрести офисное здание полезной площадью 15000 кв. м. На момент предложения оно сдается в аренду единственному арендатору, имеющему высший рейтинг платежеспособности. Ежегодная абсолютная величина арендной платы рассчитывается, исходя из ставки 14 долларов за кв. м
в год, и выплачивается авансом. Срок аренды истекает через 4 года. Арендатор уведомил хозяина, что в конце срока он освободит помещения.
По мнению оценщика, после отъезда сегодняшнего арендатора лучшим и наиболее эффективным использованием здания будет его перемоделирование под три офисных секции — площадью 5000 кв. м каждая. Есть основания полагать, что в этом случае все секции можно будет сдавать в аренду за 22 доллара за кв. м в течение пятого года. Перемоделирование здания обойдется в 25000 долларов.
Предполагается, что в течение пятого года на перестройку здания потребуется полгода, а в оставшиеся месяцы оно будет занято арендаторами в среднем на 1/3. Постоянные расходы должны составить за год 50000 долларов, операционные расходы — 15% от годовых рентных поступлений.
В течение шестого года ожидается, что пустовать будет только одна секция. Ставка арендной платы, фиксированные и операционные расходы составят 22 доллара за кв.
м, 55000 долларов и 15% соответственно.
Ожидается, что с седьмого по десятый год заполняемость возрастет до 90%. Арендная ставка за 1 кв. м составит в 7-м, 8-м, 9-м и 10-м годах 23, 24, 25 и 26 долларов соответственно. Постоянные расходы будут возрастать на 5000 долларов ежегодно, начиная с седьмого года. Доля операционных расходов останется прежней.
По оценкам, через 10 лет данное здание можно будет продать не менее чем за 4 млн. долларов.
На ближайшие 4 года, когда здание будет арендовано первым арендатором, ставка дохода принята за 9%. На вторую часть прогнозного периода ставка дохода оценивается в 10%. Для реверсии принята ставка дисконта в 11%.
Инвестору сделали предложение приобрести это офисное здание за 3 млн. долларов.
Каков ваш ответ? Используя приведенную информацию, рассчитайте текущую стоимость данного объекта.
Решение. Калькуляция арендной платы (абсолютная чистая годовая рента) с 1-го по 4-й год:
14 долларов/кв. м X 15000 кв. м – 210000 долларов.
5- й год: 22 X 15000 X 1/2 X 1/3 – 55000 долларов.
6- й год: 22 X 15000 X 2/3 = 220000 долларов.
7- й год: 23 X 15000 X 0,9 « 310500 долларов.
8- й год: 24 X 15000 X 0,9 « 324000 долларов.
9- й год: 25 X 15000 X 0,9 = 337500 долларов.
10- й год: 26 X 15000 X 0,9 – 351000 долларов.
Текущая стоимость ежегодного периодического дохода определяется по таблице.
Текущая стоимость ежегодного периодического дохода
| і | Годовая ранта | Постоянные расход | Операци онные расходы | Расходы на модернизацию | Периодиче ский поток дохода | Норма дисконтирования, % | Текущая стоимость |
| 0 | 210000 | 0 | 0 | 0 | 210000 | 9 | 210000,00 |
| 1 | 210000 | 0 | 0 | 0 | 210000 | 9 | 192660,55 |
| 2 | 210000 | 0 | 0 | 0 | 210000 | 9 | 176752,80 |
| 3 | 210000 | 0 | 0 | 0 | 210000 | 9 | 162158,53 |
| 4 | 55000 | 50000 | 8250 | 25000 | -28250 | 10 | -19295,13 |
| 5 | 220000 | 55000 | 33000 | 0 | 132000 | 10 | 81961,61 |
| 6 | 310500 | 60000 | 46500 | 0 | 204000 | 10 | 115152,68 |
| 7 | 324000 | 65000 | 48600 | 0 | 210400 | 10 | 107968,47 |
| 8 | 337500 | 70000 | 50625 | 0 | 223350 | 10 | 101173,79 |
| 9 Пол | 351000 ная текущая | 75000 СТОИМОСТЬ I | 52650 . іериодическ | 0 эго потока д | 223350 охода | 10 | 94722,20 1223255,50 |
Текущая стоимость реверсии (платежа в 4000000 долларов, ожидаемого к получению через 10 лет при ставке 11%):
0, 352184 X 4000000 = 1408737,92 доллара.
Полная текущая стоимость объекта равняется сумме текущей стоимости периодического потока дохода (1223255,50 доллара) и текущей стоимости реверсии (1408737,92 доллара):
1223255,50 * 1408737,92 = 2631993,42 доллара.
lt;
Рекомендации инвестору. Вам следует сообщить инвестору сделанные вами предположения относительно показателей доходов, расходов, ставки дохода и стоимости реверсии в течение предстоящих 10 лет. Проинформируйте инвестора, что на основании указанных предположений рыночная стоимость имущества оценивается в 2630000 долларов (округленно). Это ниже цены предложения в 3 млн. долларов. Видимо, от этого предложения придется отказаться.
1.1Простые ставки
Из формулы (1) следует (вывод формулы в задаче 20):
(8)![]() ;(9)
;(9)![]() ;(9)
;(9)
Формулу для расчета дисконта получим исходя из условия:
![]()
![]()
(10)
![]()
Вышеприведенные формулы применимы при выражении срока в годах. При выражении интервала начисления в более мелких единицах времени следует поменять в формулах n на t/K, тогда получим:
(8.1) ;(9.1)
;(9.1) ;(9.1)
;(9.1)(10.1)

- Задача
1.2Сложные ставки
(11)![]() ;(12)
;(12)![]() ;(12)
;(12)(13)
![]() (11.1)
(11.1) (11.1)
(11.1);(12.1)
 (13.1)
(13.1) (13.1)
(13.1)
- Задача
Сумма 5 млн. руб. выплачивается через 5 лет. Необходимо определить ее современную величину при условии, что применяется ставка сложных процентов 12% годовых.
Решение.
Дисконтный множитель для данных условий составит
![]()
Для каких целей необходимо дисконтировать будущие платежи? Примером ответа на этот вопрос является следующая задача.
- Задача
Вы хотите вложить свои 100 тыс. руб. в интересующую Вас финансовую операцию, которая через 3 года и 3 месяца закончится и принесет Вам 120 тыс. руб. Оцените целесообразность данного вложения, если у вас есть альтернативная возможность гарантированного размещения средств с ежеквартальным начислением процентов по номинальной ставке 10% годовых.
Решение.
Очевидно, что современная стоимость альтернативного размещения составляет 100 тыс. руб. Найдем современную стоимость дохода, который Вы можете получить по итогам финансовой операции, используя для дисконтирования в качестве ставки сравнения ставку по гарантированному размещению.
Вывод. Ваши инвестиции в интересный проект убыточны по сравнению с гарантированным использованием средств, поэтому оно не целесообразно.
2.1Учет по простой учетной ставке
Размер дисконта, или суммы учета, очевидно равен
(14)![]()
d годовая учетная ставка,
n срок от момента учета до даты погашения в годах.
Таким образом
(15)![]()
Дисконтный множитель здесь равен
(16)![]()
Из формулы (15) вытекает, что при n > 1/d величина kд и PV станет отрицательной.
Учет посредством учетной ставки чаще всего осуществляется при временной базе К = 360 дней, число дней ссуды обычно берется точным (метод 365/360). Однако в практике российских банков на текущий момент чаще применяется метод 365/365.
Для учета при сроках, измеряемых в единицах времени меньше года расчетные формулы имеют вид:
(14.1)![]() (15.1)
(15.1)![]() (15.1)
(15.1)(16.1)
![]()
- Задача
Тратта (переводной вексель) выдан на сумму 100 тыс. руб. с уплатой 17 ноября 2006г. Владелец векселя учел его в банке 23 сентября 2006г. по учетной ставке 20% (метод 365/365). Определить сумму, полученную при учете и доход банка, который он получит при предъявлении векселя.
Решение.
Оставшийся до конца срока период равен 55 дням:
| Сентябрь | 8 |
| Октябрь | 31 |
| Ноябрь | 17-1=16 |
| Всего дней: | 55 |
![]()
сумма, полученная при учете.
![]()
![]()
2.2Учет по сложной учетной ставке
В практике учетных операций иногда применяют сложную учетную ставку. В этих случаях процесс дисконтирования происходит с замедлением, так как каждый раз учетная ставка применяется не к большой конечной сумме (как при простой учетной ставке), а к сумме, уменьшенной дисконтированием на предыдущем шаге. Дисконтирование по сложной учетной ставке осуществляется по формуле
(17)![]()
d сложная годовая учетная ставка,
(18)![]() (19)
(19)![]() (19)
(19)
А при периодичности начисления дисконта меньше года:
(17.1)![]()
f номинальная годовая учетная ставка,
(18.1)![]() (19.1)
(19.1)![]() (19.1)
(19.1)
- Задача
Дисконтированный – сборник задач-экономика – методические рекомендации по решению задач по соответствующим темам…
Подборка по базе: Николаева 193гр 75 задач -1.docx, Решение логических задач – справочник.pdf, Теория вероятности. Примеры решения задач.docx, Методические рекомендации по организации внеурочной деятельности, Решение ситуационных задач.docx, цели и задачи.docx, Финансы задача.docx, 13 задача.docx, Клинические рекомендации Желтуха инф.генеза.doc, 2022. Методические материалы. 13.02.03.pdf
Дисконтированныйпотокденежныхсредств(discounted cash flow) – будущие величины денежных потоков, рассчитанные в текущих денежных единицах, исходя из ожидаемого значения ставки дисконтирования.
Риск потока денежных средств называемый риском изменения величины будущих поступлений и инвестиций, связанного с денежными финансовыми инструментами, должен учитываться в норме дисконта.
Приведение (дисконтирование) затрат и доходов заключается в определении их исходных (начальных) сумм на основе конечных сумм путем умножения фактического размера на дисконтирующий коэффициент для соответствующих норм (учетных ставок) процента и периода дисконтирования (в годах).
Дисконтирующий коэффициент – at =1/(1 r) используется для умножения планируемого размера затрат или дохода.
Дисконтирование будущих объемов инвестиций (инвестиционных затрат) и доходов (поступлений от реализации проекта) к расчетному (текущему) периоду времени с учетом нормы дисконта позволяет определить настоящую (текущую, т.е. современную) стоимость будущих денежных потоков по следующей формуле:
где Iб,, Pб – будущая стоимость инвестиций и дохода (денежного потока);
rd– дисконтная ставка (норма дисконта);
t – годы (шаги) расчетного периода (времени дисконтирования);
Из вышеприведенных формул следует, что будущая стоимость современного (настоящего) потока инвестиций или дохода (денежного потока) определяется по формулам:
Iб = Iн* (1 rd)t, или Pб=Pн* (1 rd)t,
Чистаясовременнаястоимостьбудущихинвестиций (Net present value of future investments) – современная стоимость суммы чистых стоимостей, ожидаемых по всем будущим инвестициям в инновационный проект в форме капитальных вложений.
Экономическаяэффективность инновационного проекта – относительный показатель, соизмеряющий полученный результат реализации инновационного проекта с инвестиционными затратами, обусловившими этот результат, или с ресурсами, использованными для достижения этого результата.
Примеры решения задач
Пример 9.1.
На предприятии разработан инновационный проект “НИОКР и освоение производства нового товара”, предусматривающий три варианта инвестиций в форме капиталовложений объемом 600 тыс. руб. Смета расходов на проект по вариантам и сроки осуществления инвестиций одинаковы. Структура инвестиционных затрат по годам расчетного периода различна, t – номер шага (года) расчета. Расчетным годом (t=0) является год начала финансирования инвестиций. Расчетный инвестиционный период (горизонт расчета – Т,измеряемыйколичествомшагов) – четыре года. Норма дисконта (rd) равна 10% (0,1).
Определить дисконтированную сумму инвестиций по вариантам и какой из вариантов осуществления инвестиций с учетом фактора времени является более эффективным. Исходные данные представлены в таблице.
Варианты инвестиций
в форме капиталовложенийРасчетный период (годы осуществления
инвестиций)Сумма инвестицийПервыйВторойТретийЧетвертыйПервый вариант24018012060600Второй вариант102138156204600Третий вариант150150150150600Решение:
Дисконтированная сумма инвестиций (I1 ), тыс. руб.
240 180 120 60
I1 = ──── ──── ──── ──── = 218,2 148,8 90,2 41,1 = 498,3
1 0,1 (1 0,1)2 (1 0,1)3 (1 0,1)4
2. Дисконтированная сумма инвестиций (I2 ), тыс. руб.
102 138 156 204
I2 = ──── ──── ──── ──── = 92,7 114 117,3 139,7 = 463,7
1 0,1 (1 0,1)2 (1 0,1)3 (1 0,1)4
3. Дисконтированная сумма инвестиций (I3), тыс. руб.
150 150 150 150
I3 = ──── ──── ──── ──── = 136,4 124 112,8 102,7 = 475,9
1 0,1 (1 0,1)2 (1 0,1)3 (1 0,1)4
Наиболее эффективным вариантом осуществления инвестиций является второй, с наименьшей дисконтированной суммой инвестиций (I2).
Задачи для самостоятельного решения
Задача 9.1. Оценить потребность в инвестициях (Iп) в форме капитальных вложений (тыс. руб.) в текущем году и общую потребность для осуществления инновационного проекта предприятия, планируемую на следующий год (Iп = Iо1 Iо2 Iо3 … Iоn) . Исходные данные о необходимых для проекта инвестициях, связанных с приобретением активов: оборудования, вычислительной техники, транспортных средств, нематериальных активов представлены в таблице. В расчете использовать текущий курс доллара США Центробанка России. Определить коэффициент изменения суммы инвестиций на планируемый год в сравнении с текущим годом.
ПоказателиТекущий годПлан на следующий годИнвестиции в форме капитальных вложений (I), всего, в том числе: – приобретение оборудования:5394 тыс. руб. и
105845$18555 тыс. руб. и
65 550 $ – вычислительной техники2000 тыс. руб. – транспортных средств200 тыс. руб. – на приобретение нематериальных активов (программного обеспечения)
640 тыс. руб. – прочие капвложения –Задача 9.2. Определить инвестиции в форме капитальных вложений для реализации инновационного проекта на планируемый период (год) на основе данных задачи 9.1 при дополнительных данных о вложении капитала: в оборудование – уменьшится в 2 раза;
в транспортные средства – снизится на 15%;
в нематериальные активы – потребность отсутствует;
прочие капитальные вложения составят 609 тыс. руб.
Задача 9.3. Определить объем инвестиций в форме капитальных вложений с дисконтированием на момент начала инвестирования, требуемый на первый и второй год разработки, экспериментальных исследований, документального оформления и утверждения инновационного проекта, а также на третий год расчетного периода, в котором планируется освоение производства нового товара и выведение его на целевой сегмент рынка.
Исходные данные: расчетным годом принимается первый год расчетного периода; установленная общая потребность в инвестициях на указанные мероприятия 143800 тыс. руб.; предполагается неравномерное инвестирование по годам в двух вариантах: 1-й вариант: первый год 60% от общей потребности, второй год-20%, третий год 20%; 2-й вариант: первый год 25% от общей потребности, второй год-60%, третий год – 15%. Норма дисконта (rd) равна 11 % (0,11). Сделать оценку – какой из вариантов структуры инвестиционных затрат на проект в большей степени будет способствовать повышению эффективности его разработки и освоения.
Задача 9.4. Предприятие планирует реализовать инновационный проект по разработке нового товара, освоению его производства и выведению товара на рынок. Предполагаемый на три года объем инвестиций в форме капитальных вложений при равномерном по годам финансировании объектов инвестирования следующий:
1. Маркетинговые исследования 945 тыс. руб.;
2. Ноу-хау 1280 тыс. руб.;
3. НИОКР 2135 тыс. руб.;
4. Разработка новых технологий 1428 тыс. руб.;
5. Проектирование технологического оснащения 725 тыс. руб.;
6. Приобретение оборудования 1666 тыс. руб.;
7. Создание норматива оборотных средств 593 тыс. руб.;
8. Рекламная компания 1376 тыс. руб.
Определить потребность в инвестициях в инновационный проект предприятия:
– по каждому объекту инвестирования по годам без дисконтирования;
– на каждый планируемый год в целом по всем объектам инвестирования без дисконтирования и с дисконтированием. Норма дисконта (rd) равна 11 % (0,11). Вышеуказанные исходные данные и рассчитанные показатели занести в таблицу.
Объект инвестированияВсего инвестиций на 3 годав том числе по годампервыйвторойтретий1. …8.Общая потребность в инвестициях
без дисконтированияПотребность в инвестициях
с дисконтированиемЗадача 9.5. Определить в каком из двух вариантов инновационного проекта предприятия по модернизации действующего производства сумма дисконтированных инвестиций в форме капитальных вложений составит меньшую величину.
Норма дисконта (rd) равна 12 % (0,12). Исходные данные представлены таблице.
ПоказателиВариантыIIIОбщий объем инвестиций, тыс. руб.,
в том числе:
первый год
второй год
третий год
четвертый год45200
11300
11300
11300
1130045200
–
15000
16000
14200Задача 9.6. В соответствии со стратегией развития предприятия планируется реализовать инновационный проект по обновлению технологии изготовления и повышения качества товара, пользующегося спросом у покупателей, который прорабатывается в двух вариантах. Смета расходов на проект по вариантам и срок осуществления инвестиций одинаковы, но структура инвестиционных затрат различна по годам расчетного периода. Расчетный период 3 года. Расчетным годом принимается первый год расчетного периода. Проектом предусмотрены два варианта вложения капитала размером 1350 тыс. руб. В первом варианте предусмотрено равномерное вложение капитала по годам, во втором – в следующем соотношении: первый год – 50%, во второй год – 40%, в третий год – 10% от общей суммы инвестиций.
Определить чистуюсовременнуюстоимостьбудущихинвестиций (дисконтированную сумму инвестиций (Iq) с учетом фактора времени) при норме дисконта (rd) 10% по годам. Обосновать выбор более эффективного варианта вложения инвестиционного капитала.
Задача 9.7. Определить чистуюсовременнуюстоимостьбудущихинвестиций как дисконтированную сумму инвестиций в инновационный проект со сроком его реализации 4 года, при норме дисконта 11%.
Планируемая сумма инвестиций в проект 2880 тыс. руб., в качестве расчетного года принимается год начала финансирования инвестиций.
Предусматривается следующий порядок осуществления инвестиций:
Первый вариант: первый год – 30%, второй год – 40%, третий год – 10% и четвертый год – 20% от планируемой суммы инвестиций.
Второй вариант: равными долями по годам.
Третий вариант: первый год – 40%, второй, третий и четвертый годы – равными долями от оставшейся суммы инвестиций.
Задача 9.8. В планируемый к разработке и реализации инновационный проект предприятия по освоению наукоемкого производства требуется 84600 тыс. руб. инвестиций. Расчетный период – 5 лет (t=0, 1, 2, 3, 4). Вложение инвестиционного капитала осуществляется в первые два года расчетного периода по 50%. Ежегодные планируемые поступления от продаж нового продукта со следующего (третьего) года составят соответственно 72500, 105200, и 179800 тыс. руб. Норма дисконта (rd) равна 10 % (0,1).Оценить двумя методами: без дисконтирования и с дисконтированием (то есть с учетом фактора времени), уровень обоснованности установленного объема инвестиций в форме капитальных вложений с точки зрения их окупаемости.
- Чистый_доход_от_осуществления_инновационного_проекта_и_срок_окупаемости_инвестиций_в_проект’>Чистый доход от осуществления инновационного проекта и срок окупаемости инвестиций в проект
К основным показателям, используемым для оценкиэкономическойэффективности инновационных проектов предприятия, соизмеряющей полученный результат (доход, прибыль) от их реализации с инвестиционными затратами, обусловившими этот результат, относится чистый доход, чистый дисконтированный доход, чистый денежный поток, срок окупаемости инвестиций в форме капитальных вложений и другие.
Чистыйдоход – сумма дохода от реализации инновационного проекта за каждый год за вычетом сумм затрат, возникающих в ходе реализации проекта. Чистый доход определяется как сумма чистой прибыли (прибыли от реализации товара после налогообложения) и амортизации оборудования, применяемого в рамках проекта.
Чистыйдисконтированныйдоход – современная (приведенная) стоимость суммы чистых стоимостей доходов, ожидаемых по всем будущим поступлениям по годам реализации инновационного проекта.
Для сопоставления альтернативных инновационных проектов проводится дисконтирование будущих доходов, что позволяет оценить планируемые доходы от их реализации с учетом современной стоимости денежных средств. Если инвестиции в течение “n” лет будут приносить годовой доход “P”, то общий дисконтированный доход (PV) рассчитывается по формуле:Pt
PV=
t=1 (1 rd) t
Чистыйденежныйпоток(net cash flow) – разность между суммами поступлений и инвестиционных затрат за определенный период времени. Чистый денежный поток рассчитывается с учетом выплат, дивидендов и налогов.
При сопоставлении альтернативных инновационных проектов и выборе из их числа наиболее эффективного используется метод чистой приведенной стоимости – Net present value method (NPV метод). Это – инвестиционное правило, согласно которому инвестиции в проект следует производить, если их чистая приведенная (текущая, т.е. современная) стоимость имеет положительное значение. Современная стоимость – текущая сумма наличными, эквивалентная размеру инвестиций или доходов, которые должны быть получены в будущем. Чистая современная стоимость используется для оценки инновационных проектов, требующих инвестиций в форме капитальных вложений. Проекты с отрицательной чистой современной стоимостью следует отвергать.
При выборе из альтернатив инновационных проектов используется метод окупаемости (recoupment method) – метод оценки инновационных проектов, требующих инвестиций в форме капитальных вложений, согласно которому предпочтение должно отдаваться проектам с наименьшим сроком окупаемости.
Срококупаемости(paybackperiod – PP) инвестиций в форме капитальных вложений – период, в течение которого возмещается первоначальная стоимость проекта независимо от временной стоимости денег.
PP – число лет, которое необходимо для возмещения первоначальных (исходных) инвестиций за счет прибыли от реализации инновационного проекта.
Величина срока окупаемости зависит от равномерности или неравномерности осуществления инвестиций и распределения по годам прогнозируемых доходов от инвестиций.
Срок окупаемости инвестиций (PP), достигаемыйв течение одного интервала планирования (одного года), а также при равномерном распределении денежных поступлений по годам определяется без дисконтирования отношением инвестиций к полученной прибыли по формуле:
I
PP = ,
Pt
гдеPt-чистый доход от реализации инновационного проекта (чистая прибыль годовая плюс амортизация за год), руб. / год.При интервале планирования более одного года для расчета срока окупаемости, характеризующего период возврата капитала (Capital recovery period), требуется дисконтирование. Если денежные доходы поступают по годам неравномерно, то используется алгоритм расчета PP прямым подсчетом числа лет, в течение которых капитальные вложения будут погашены кумулятивным доходом. Срок окупаемости инвестиций равен периоду времени (числу лет), за который суммарные денежные поступления (кумулятивный доход) превысят величину инвестиций:
Т
PP – это число лет, при котором Pt > I, Т-минимально
t=0
Срококупаемости инвестиций в форме капитальных вложений с учетом дисконтирования тесно связан с NPV инновационного проекта, так как определяется на основе тех же показателей.
Примеры_решения_задач__Пример_9.2.’>Примеры решения задач
Пример 9.2.
Определить чистый доход (сумму чистой прибыли и амортизации), ожидаемый от реализации инновационного проекта и срок окупаемости инвестиций в форме капитальных вложений в проект, который предприятие планирует внедрить в пределах двух лет. Исходные данные представлены в таблице.
ПоказателиПланируемый периодпервый годвторой год1. Объем инвестиций в форме капиталовложений, тыс. руб.450015002. Объем реализации товара (без НДС), тыс. руб.850095003. Себестоимость реализуемого объема товара, тыс. руб.
в том числе амортизация, тыс. руб. 5900
8506700
8804. характеристика организации пивоваренная компания «Балтика», часть CarlsbergGroup, один из крупнейших производителей товаров народного потребления России, с 1996 год”>Налоги и прочие отчисления от прибыли, тыс. руб.310405Решение:
1. Общий объем инвестиций в форме капиталовложений (Iобщ) без дисконтирования, тыс. руб.
Iобщ = 4500 1500 = 6000
2. Прибыль от реализации товара (объем реализации минус себестоимость), тыс. руб.
первый год 8500 – 5900 = 2600
второй год 9500 – 6700 = 2800
3. Чистая прибыль (прибыль от реализации минус налоги и прочие отчисления от прибыли), тыс. руб.
первый год 2600 – 310 = 2290
второй год 2800 – 405 = 2395
4. Чистый доход (чистая прибыль плюс амортизация), тыс. руб.
первый год 2290 850 = 3140
второй год 2395 880 = 3275
5. Срок окупаемости (PP) инвестиций в форме капиталовложений (без учета дисконтирования) отражает минимальный период времени, начиная с которого инвестиции покрываются суммарной величиной чистого дохода.
Срок окупаемости определяется следующим образом:
за первый год реализации проекта инвестиции окупятся за счет чистого дохода в сумме 3140,0 тыс. руб.;
требуемый объем инвестиций в форме капиталовложений на реализацию проекта составляет 6000 тыс. руб., который больше суммы дохода за первый год. Это означает, что за первый год инвестиции полностью не окупаются;
за счет чистого дохода второго года (3275,0) необходимо окупить инвестиции в сумме 2860,0 тыс. руб. (6000,0 – 3140,0 = 2860,0);
коэффициент определяющий временной интервал (количество месяцев) второго года (Квр), когда чистый доход становится неотрицательным рассчитывается следующим образом: Квр = 2860,0 / 3275,0 = 0,87. Число месяцев (Чмес) определяется по формуле: (Чмес) =Квр* 12 = 0,87 * 12= 10мес.
Следовательно, срок окупаемости (PP) инвестиций в форме капиталовложений (без учета дисконтирования) составит 1 год 10 мес.
Пример 9.3. Определить чистый дисконтированный доход от осуществления инновационного проекта по освоению нового производства на предприятии и срок окупаемости инвестиций в форме капитальных вложений. Норма дисконтирования равна 0,12. Исходные данные представлены в таблице.
Показатели
Планируемый периодпервый годвторой годтретий год1. Объем инвестиций в форме капиталовложений, тыс. руб.1020025000-2. Объем реализации товара (без НДС), тыс. руб.870017400193003. Себестоимость реализуемого объема товара тыс. руб.
в том числе амортизация, тыс. руб.6200
60011400
72022900
7004. Налог на прибыль и другие выплаты, тыс. руб.400700730Решение:
1. Общий объем инвестиций в форме капиталовложений (I) с учетом дисконтирования, тыс. руб.:
10200 2500
I = ──── ──── = 9107 1994 = 11101
(1 0,12) (1 0,12)2
2. Прибыль от реализации товара, тыс. руб.:
1-й год 8700 – 6200 = 2500
2-й год 17400 – 11400 = 6000
3-й год 19300 – 11900 = 7400
3.Чистая прибыль (прибыль от реализации товара минус налог на прибыль), тыс. руб.:
1-й год 2599 – 400 = 2100
2-й год 6000 – 700 = 5300
3-й год 7400 – 730 = 6670
4. Чистый доход (чистая прибыль плюс амортизация), тыс. руб.:
1-й год 2100 600 = 2700
2-й год 5300 720 = 6020
3-й год 6670 700 = 7370
5. Чистый дисконтированный доход, тыс. руб.:
2700
1-й год ──── = 2410,7
(1 0,12)
6020
2-й год ──── = 4801,0
(1 0,12)2
7370
3-й год ──── = 5249,2
(1 0,12)3
6. Срок окупаемости инвестиций в форме капиталовложений (PP) с учетом дисконтирования, тыс. руб.:
за первый год окупятся 2410,7 тыс. руб.
за второй год окупятся 2410,7 4801,0 = 7211,7 тыс. руб.
за третий год необходимо окупить 11101,0 – 7211,7 = 3889,3 тыс. руб.
Эта сумма окупится за 0,74 года (3889,3 5249,2) или 9мес
(12 0,74).
Следовательно, срок окупаемости (PP) составит 2 года 9 месяцев.
Задача – срок окупаемости проекта простым способом и с учетом дисконтирования | инфо экономика
Вариант Б
Коэффициент дисконтирования при ставке 10%:
1-й год Кд = 1 / (1 0,1)^1 ≈ 0,909
2-й год Кд = 1 / (1 0,1)^2 ≈ 0,826
3-й год Кд = 1 / (1 0,1)^3 ≈ 0,751
4-й год Кд = 1 / (1 0,1)^4 ≈ 0,683
5-й год Кд = 1 / (1 0,1)^5 ≈ 0,621
6-й год Кд = 1 / (1 0,1)^6 ≈ 0,564
7-й год Кд = 1 / (1 0,1)^7 ≈ 0,513
8-й год Кд = 1 / (1 0,1)^8 ≈ 0,467
9-й год Кд = 1 / (1 0,1)^9 ≈ 0,424
10-й год Кд = 1 / (1 0,1)^10 ≈ 0,386
Для нахождения дисконтированного дохода необходимо каждый годовой доход умножить на соответствующий коэффициент дисконтирования. Результаты расчетов приведены в таблице ниже:
| Период времени | Стоимость проекта, тыс. руб. | Денежные поступления, тыс. руб. | Коэффициент дисконтирования | Дисконтированный доход, тыс. руб. | Кумулятивная стоимость, тыс. руб. |
| 0 | 600 | — | — | — | -600 |
| 1 | — | 95 | 0,909 | 86 | -514 |
| 2 | — | 95 | 0,826 | 79 | -435 |
| 3 | — | 95 | 0,751 | 71 | -364 |
| 4 | — | 95 | 0,683 | 65 | -299 |
| 5 | — | 95 | 0,621 | 59 | -240 |
| 6 | — | 95 | 0,564 | 54 | -186 |
| 7 | — | 95 | 0,513 | 49 | -138 |
| 8 | — | 95 | 0,467 | 44 | -93 |
| 9 | — | 95 | 0,424 | 40 | -53 |
| 10 | — | 95 | 0,386 | 37 | -16 |
| Итого | 600 | 950 | 584 |
Срок окупаемости проекта простым способом составляет: 600 / 95 = 6,32 года или 6 лет и 4 месяца (6 0,32*12).
Как видно из таблицы, кумулятивный денежный поток отрицателен на конец 10 года, что говорит о том, что с учетом дисконтирования срок окупаемости превысит 10 лет. Срок окупаемости с учетом дисконтирования составит: 10 (16/95*(1/(1 0,1)^11)) = 10,48 лет или 10 лет и 6 месяцев (10 0,48*12).
Ответ: срок окупаемости проектов А и Б простым способом составит 6 лет и 4 месяца, а с учетом дисконтирования проект А окупится за 9 лет и 2 месяца, а проект Б – за 10 лет и 6 месяцев.
Задачи с решениями по финансовой математике
Задачи с решениямипофинансовойматематике
1. Банкначисляет 50 рублейобыкновенногопростогопроцентазаиспользование 3000 рублей в течение 60 дней. Какованормапростогопроцентатакойсделки?
Решение:
Простойпроцентвычисляетсяпоформуле:
R = iP * (t/T);
50 =i 3000* (60/365);
I = 365*50 /(3000*60) = 0,1014 (10,14%)
Или:
S = P (1 i); (50 3000) = 3000 (1 i); 3050 = 3000 3000 i; 50/3000 = i; i = 0,0167 (1,67 %) – за 60 дней (два месяца); за год: i = 0,0167*365/60 = 0,101388 (10,14%);
Решение:
В случаепростогодисконта:
P = S (1 – nd);
Выручка:
P = 100000 (1 – 0,035* 72/365)= 100000 *0,993 = 99300 руб.
Дисконтсоставит:
100000 – 99300 = 700 руб.
Решение:
Sn = P(1 i)n
2 = 1 (1 i)12
(1 i)12 =2
Прологарифмируемполученноевыражение:
12 lg (1 i) = lg2; lg2 = 0,3
12 lg (1 i) = 0,3
Lg (1 i) = 0,0025; (1 i) = 1, 06; i = 0,06 (6%)
Можнобылонеделатьтакихсложныхрасчетов. В учебникахпобанковскомуделу и ценнымбумагамприлагаютсятаблицы, в которыхпоказываетсябудущаястоимостьединицы при определеннойгодовойставкечерезопределенныйпериодвремени.
Единица удваивается через 12 лет при 6% годовых.
Решение:
Эквивалентная процентная ставка:
J = (1 i)m/n -1 =(1 0,05)10/3 -1;
(1 i)m = (1 j)n = (1 0,05)10
(1 j)n = (1 0,05)10 = 1,6289
Отсюда:
(1 i)3 =1,6289; (1 i) = 1,1768; i = 0,1768 ≈ 17,7%
По ставке сложного процента:
При n = 3 и 5 %
Будущая стоимость единицы: 1,1576
Sn = P(1 i)n
Р = 10000/1,6289 = 6139,11 руб.
Тогда: 6139,11*1,1576 = 7139,63 руб.
Решение:
Полагающийся аннуитет:
500 000 = R *[(1 0,015 )4*5 -1] /0,015 * (1 0,015);
(1,34685-1)/0,015* 1,015 = 23,47044;
Отсюда: R = 500000/ 23,47044= 21303,4 руб.
Решение:
По формуле обыкновенного общего аннуитета:
S = 500 * ((1 0,04)5*1 -1)/ ((1 0,04)1/4 -1 ) = 500* 0,2167/0,00985 = 11 000 руб.
Решение:
Вечная рента – это аннуитет, платежи которого продолжаются в течение неограниченного времени
Эквивалентная процентная ставка равна:
J =(1 i)m/p -1 = (1 0,03)4/12 -1= 1,0108 -1 = 0,0108
M=4; p =12
А =R/j = 1500/0,0108 = 138888,88 руб.
Годовых?
Решение:
Доход по облигации представляет собой поток периодических платежей в конце каждого года (простой аннуитет) и разовую выплату в конце всего срока действия облигации.
С=N = 100000 руб.,
Ежегодные выплаты: R = 5000 руб., i =0,03
Цена покупки:
Р = 5000* [ 1-(1 0,03)-15]/0,03 100000 (1 0,03)-15 = 5000 *(1-1/1,5580)/0,03 100000(1/1,0315) = 5000 * 11,9384 100000*0,64185 = 123877 руб.
Решение:
Рассчитаем будущюю стоимость 20000 рублей через 3 года, под 17% годовых.
FV = 20000 * (1 0,17)3 = 32032 рубля.
Ответ. Получить 35000 рублей через 3 года является более выгодным решением, при данном значении процентной ставки.
Преобразуем формулу к следующему виду:
(1 r)n = FV / PV и подставим значения;
1,14n = 20000 / 1000 = 20, отсюда n = log 1,14 20 = 22,86 года.
Ответ. 1000 рублей нарастится до 20000 рублей при 14% годовой ставке за 22,86 года.
При расчете числа лет необходимо учитывать, что в формуле подразумевается целое число лет и цифры, рассчитываемые после запятой, имеют приблизительные значения, характеризующие близость к целому значению лет.
Нарастились до 30 000 рублей, за срок вклада 5 лет?
Преобразуем формулу к следующему виду:
R = (FV / PV)1/n – 1 и подставим значения;
R = (30 000 / 10 000)1/5 – 1;
R = 0,24573 или 24,573 %.
Ответ. 10 000 рублей нарастятся до 30 000 рублей за 5 лет при ставке ссудного процента 24,573%
Решение.
Способ 1.
![]() ,
,
K’ = K I = 4000 44=4044,
где K – капитал или заем, за использование которого заемщик выплачивает определенный процент;
I – процентный платеж или доход, получаемый кредитором от заемщика за пользование денежной ссудой;
P – процентная ставка, показывающая сколько д. е. должен заплатить заемщик за пользование 100 ед. капитала в определенном периоде времени (за год);
D – время, выраженное в днях.
360 – число дней в году.
Способ 2.
Время t = 80/360 = 2/9.
K’ = K K×i×t = 4000(1 0.05×2/9) = 4044,
Где i – процентная ставка, выраженная в долях единицы,
T – время, выраженное в годах.
Решение
2×K = I.
2×K = K×9×g/100,
G = 2×100/9 = 22.22
14. Величина предоставленного потребительского кредита – 6000 д. е., процентная ставка – 10% годовых, срок погашения – 6 месяцев. Найти величину ежемесячной выплаты (кредит выплачивается равными долями).
Решение
Таблица – План погашения кредита (амортизационный план)
Месяц | Долг | Процентный | Выплата долга | Месячный взнос |
6000 | 10% | |||
1 | 5000 | 50 | 1000 | 1050 |
2 | 4000 | 42 | 1042 | |
3 | 3000 | 33 | 1033 | |
4 | 2000 | 25 | 1025 | |
5 | 1000 | 17 | 1017 | |
6 | ¾ | 8 | 1008 | |
175 | 6000 | 6175 |
Объяснение к таблице
Месячная выплата основного долга составит:
K / m = 6000/6 = 1000.
Месячный взнос представляет собой сумму выплаты основного долга и процентного платежа для данного месяца.
Процентные платежи вычисляются по формуле:
![]() ,
,
Где I1 – величина процентного платежа в первом месяце;
P – годовая процентная ставка, %.
Общая величина выплат за пользование предоставленным кредитом:
![]() =175.
=175.
Общая величина ежемесячных взносов:
![]() =1029.
=1029.
Годовых. Найти дисконт и дисконтировать величину векселя.
Решение
Так как нам известна номинальная величина векселя, дисконт, находим по формуле:
![]() =409,
=409,
Где Kn – номинальная величина векселя;
D – число дней от момента дисконтирования до даты погашения векселя;
D – процентный ключ или дивизор (D = 3600/p = 36000/8 = 4500).
Дисконтированная величина векселя равна разности номинальной стоимости векселя и дисконта (процентного платежа):
20000 – 409 = 19591.
D) годовых. Найти конечную сумму капитала, если расчетный период составляет: а) 3 месяца; б) 1 месяц.
Решение
При декурсивном (d)расчете сложных процентов:
Kmn = K×Ip/mmn, Ip/m = 1 p/(100×m),
Где Kmn – конечная стоимость капитала через N лет при p% годовых и капитализации, проводимой M раз в год.
А) K = 20000×I2.54 = 20000×(1 10/(100×4))4 = 20000×1.104 = 22076 д. е.
Б) K = 20000×I10/1212 = 20000×(1 10/(100×12))12 = 20000×1.105 = 22094 д. е.
При антисипативном (a) способе расчета сложных процентов:
Kmn = K×Iq/mmn, Iq/m = 100m/(100m – q),
Где q – годовой прцент.
А) K = 20000×(100×4/(100×4 – 10))4 = 20000×1.107 = 22132 д. е.
Б) K = 20000×(100×12/(100×12 – 10))12 = 20000×1.106 = 22132 д. е.
Решение
 = 6.779%.
= 6.779%.
Решение
Сначала для годовой процентной ставки 8% определим процентную уравнивающую ставку:
![]() =1.9427%
=1.9427%
Затем полученную уравнивающую ставку поместим в следующую формулу:
Svmn = u× ![]() , где rk = 1 pk/100,
, где rk = 1 pk/100,
Где v – число вкладов в расчетном периоде,
n – число лет,
m – число капитализаций в год.
Тогда
Rk = 1 1.9427/100 = 1.0194
S4×10 = 500× ![]() = 500×60.8157 = 30407.84 д. е.
= 500×60.8157 = 30407.84 д. е.
Решение
![]() ,
,
U1 = u×I2%4 / III2% = 2000×1.0824 / 4.204 = 514.93 д. е.
Snm = 514.93×III2%3×4 2000 = 514.93×13.6803 2000 =
= 9044.41 д. е.
D) составляет 8%.
Решение
K0 = Kn×r-n = Kn×II8 = Kn×(1 p/100)-n = 200000×(1 8/100)-20 =
= 200000×0.21454 = 42909 д. е.,
Где r = (1 p/100) – сложный декурсивный коэффициент.
Постнумерандо, процентная ставка – 4% годовых, капитализация ежегодная.
Решение

Постнумерандо по 5000 д. е. при 8% годовых, если капитализация осуществляется каждые полгода.
Решение
При ежегодной капитализации:
C0 = a×IVpn = 5000×IV8 = 5000×6.71=33550
Решение
Таблица – План погашения займа (амортизационный план)
Год | Долг | Процентный | Выплата долга | Аннуитет |
1 | 20000 | 400 | 1826.53 | 2226.53 |
2 | 18173.47 | 363.47 | 1863.06 | |
3 | 16310.41 | 326.21 | 1900.32 |
Пояснения к таблице
Аннуитет вычисляем по формуле:
A = K×Vpn = 20000×V2 = 20000×0.1113 = 2226.53 д. е.
Чтобы определить выплату задолженности b1, вычисляем величину процентного платежа I:
I1 = K1×p/100 = 20000×2/100 = 400 д. е.
Выплата задолженности представляет собой разницу между аннуитетом и процентным платежом:
B1 = a – I1 = 2226.53 – 400 = 1826.53 д. е.
Таким образом, после первого года долг сократится на 1826.53 д. е. Остаток долга равен:
K2 = 20000 – 1826.53 = 18173.47 д. е.
Вычислим процентный платеж на остаток долга:
I2 = 18173.47×2/100 = 363.47 д. е.
Вторая выплата составит:
B2 = a – I2 = 2226.53 – 363.47 = 1863.06 д. е.
Долг уменьшится на величину 1863.06, остаток долга составит:
K3 = 18173.47 – 1863.06 = 16310.41 д. е.
Далее
I3 = 16310.41×2/100 = 326.21 д. е.
Третья выплата задолженности составит:
B3 = a – I3 = 2226.53 – 326.21 = 1900.32 д. е.
Решение:
Вывод формулы для простой ставки процентов: ![]()
![]()


Ответ: простая ставка процентов равна 180%.
5. Кредит в размере 15 000 руб. выдан с 26.03 по 18.10 под простые 24% годовых. Определить размеры долга для различных вариантов начисления процентов.
Решение:
Размер долга:
 ;
;
1) «английская практика»: Т=365 или 366 дней.
![]() (дней)
(дней)
 (руб.)
(руб.)
2) «французская практика»: T=360 дней.
![]() (дней)
(дней)
 (руб.)
(руб.)
3) «германская практика»: T=360 дней.
![]() (дня)
(дня)
 (руб.)
(руб.)
Ответ: размер долга составляет:
– согласно «английской практике»: 17 031,781 руб.;
– согласно «французской практике»: 17 060 руб.;
– согласно «английской практике»: 17 020 руб.
I квартал ссудный процент 24%, а в каждом последующем квартале процентная ставка по ссуде увеличивается на 3%. Определить сумму к возврату в банк, если ссуда выдана на год и составляет 15 000 руб.(простые проценты)
Решение:
![]()
![]()
![]()
![]()
T = 1 год = 360 дней PV = 15 000 руб. ![]() 30×3 = 90 дней
30×3 = 90 дней
Сумма начисленных процентов:
 ;
;
![]()
![]()
![]()
![]()
![]()
Сумма к возврату:
![]()
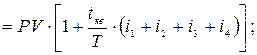

= 19 275 (руб.)
Ответ: сумма к возврату в банк составит 19 275 руб.
Решение:
PV = 15 000 руб. N = 2 года J = 16% = 0,16 M = 2
Сумма на счёте клиента к концу срока:

 20 407,334 (руб.)
20 407,334 (руб.)
Ответ: сумма на счёте клиента к концу срока составит 20 407,334 руб.
Годовых. Определить дисконтированную величину, то есть сумму, полученную владельцем векселя, и величину дисконта.
Решение:
FV = 19 000 руб. T = 1 год = 360 дней T = 60 дней N = 1 год D = 60% = 0,6
Величина дисконта:
![]()
![]() (руб.)
(руб.)
Сумма, полученная владельцем векселя:
PV = FV – D ;
PV = 19 000 – 1 900 = 17 100 (руб.)
Ответ:
– величина дисконта равна 1 900 руб.;
– сумма, полученная владельцем векселя, равна 17 100 руб.
N = 1 год).
Решение:
I = 24% = 0,24
N = 1 год
Эквивалентная годовая учётная ставка:
![]() ;
;

Ответ: эквивалентная годовая учётная ставка равна 19,4%.
Решение: FV = 19 000 руб. j = 16% = 0,16, m = 4, n = 1,5 года = ![]() года.
года.
Сумма вклада:

 15 015,976 (руб.)
15 015,976 (руб.)
Ответ: сумма вклада равна 15 015,976 руб.
Решение: N = 1 год
1) M = 4, J =24% = 0,24
2) M = 2, J =26% = 0,26
3) M = 12, J = 20% = 0,2
Эффективная процентная ставка:

при N=1 год:  ;
;



Ответ: выдача кредитов под 26% годовых с полугодовым начислением процентов банку выгоднее, т. к. эффективная годовая процентная ставка в этом случае больше (сумма кредита возрастает на 27,7% за год).
Годовых. Полугодовой уровень инфляции составил 3%. Определить реальную годовую ставку процентов с учётом инфляции.
Решение: n = 1 год i = 24% = 0,24 ![]() = 3% = 0,03 N = 2
= 3% = 0,03 N = 2
Индекс цен:
![]()
![]()
Реальная годовая процентная ставка:


Ответ: реальная годовая ставка процентов равна 16,9%.
Решение: ![]() = 3% = 0,03 n = 1
= 3% = 0,03 n = 1 ![]() = 3% = 0,03 n = 1
= 3% = 0,03 n = 1 = 10% = 0,1
Вывод формулы для процентной ставки:

![]()
![]()
Ответ: нужно назначить ставку процентов по вкладам, равную 13,3%.
Решение: ![]() N = 12 месяцев
N = 12 месяцев
Индекс цен:
![]()
![]()
Уровень инфляции:
![]()
![]()
Ответ: уровень инфляции за год равен 42,6%.
Решение: PV = 15 000 руб. j = 72% = 0,72 m = 12 месяцев n = 6/12 года p = 3% = 0,03,
N = 6 месяцев
Реальная покупательная способность вклада через определённое время:



(руб.)
Реальный доход вкладчика:
![]()
![]() (руб.)
(руб.)
Ответ: реальный доход вкладчика равен 2 819,811 руб.
S1=19 000 руб., S2=20 000 руб., S3=21 000 руб. в конце 1-го, 3-го и 5-го годов. По новому графику платежей вносится две суммы: S4=22 000 руб. в конце 2-го года и S5 в конце 4-го года. Ставка банковского процента 5%. Определить S5.
Дано: ![]()
Суммы платежей,
S1=19 000S4 =22 000S2=20 000S5 – ?S3=21 000 руб.
|__________|__________|__________|__________|__________|
0 1 2 3 4 5 Сроки платежей,
Годы
![]()
![]()
наращение дисконтирование
На рис. отмечены: Полужирным шрифтом – исходный график платежей, Курсивом – новый график платежей. Моментом приведения выбран год, совпадающий с годом платежа суммы ![]() :
: ![]() :
: 4 года.
Решение:
Уравнение эквивалентности: графики платежей будут эквивалентны, если сумма приведённых на какую-либо дату (на момент приведения) платежей одного графика будет равна сумме платежей другого графика, приведённых на ту же дату при неизменной ставке процентов:
![]()
Коэффициент приведения (наращения или дисконтирования):
![]()
Где: N – число лет до момента приведения:
N = N0 – Ni,
Где: Ni – срок I-го платежа.
При ![]() – коэффициент наращения;
– коэффициент наращения;
При ![]() – коэффициент дисконтирования;
– коэффициент дисконтирования;
При ![]()
![]()
![]()
![]()
(руб.)
Ответ: сумма второго платежа по новому графику платежей равна 38 739,875 руб.
Решение: i = 5% = 0,05 n = 6 лет FVA = 19 000 000 руб.
Размер ежегодных платежей:


(руб.)
Ответ: размер ежегодных платежей равен 2 793 331,894 руб.
Решение: R = 19 000 руб. N = 2 года I = 5% = 0,05
Величина будущего фонда:

 (руб.)
(руб.)
Ответ: величина будущего фонда равна 38 950 руб.
Годовых.
Решение: R = 1 800 руб. j = 48% = 0,48 m = 12 n = 1 год
Авансовая приведённая сумма аренды:



 (руб.)
(руб.)
Ответ: равноценный платёж, взимаемый за год вперёд, равен 17 568,858 руб.
Полугодовых купона доходностью 20% годовых каждый. Рассчитать цену её первоначального размещения, приняв ставку сравнения 16%.
Решение: N = 2 года N = 1 000 руб. M = 2 J = 16% = 0,16 Q = 20%
Цена первоначального размещения облигации:



 1 066,243 (руб.)
1 066,243 (руб.)
Ответ: цена первоначального размещения облигации равна 1 066,243 руб.
Решение: ![]()
![]()
![]() дней Т = 360 дней
дней Т = 360 дней
1) доходность по схеме простых процентов:


2) доходность по схеме сложных процентов:


Ответ:
– доходность по схеме простых процентов равна 180%;
– доходность по схеме сложных процентов равна 342,1%.
Решение: I = 5% = 0,05 N = 5 лет PVA = 1 500 000 руб.
1) амортизация займа, погашаемого равными суммами
Сумма погашения основного долга: ![]()
![]() (руб.)
(руб.)
Сумма срочной уплаты: ![]()
Остаток долга на начало периода: ![]()
Таблица –
2) амортизация займа, погашаемого равными срочными уплатами
Срочный платёж:


(руб.);
Сумма процентов: ![]()
Погасительный платёж: ![]()
Остаток долга на начало периода: ![]()
Таблица –
№ Года К | Остаток долга на начало периода
| Остаток долга на конец периода,
| Срочный платёж R, руб. | Сумма процентов | Погасительный платёж |
1 | 1 500 000,00 | 1 228 537,80 | 346 462,20 | 75 000,00 | 271 462,20 |
2 | 1 228 537,80 | 943 502,49 | 346 462,20 | 61 426,89 | 285 035,31 |
3 | 943 502,49 | 644 215,42 | 346 462,20 | 47 175,13 | 299 287,07 |
4 | 644 215,42 | 329 963,99 | 346 462,20 | 32 210,77 | 314 251,43 |
5 | 329 963,99 | -0,01 | 346 462,20 | 16 498,20 | 329 964,00 |
Итого: | Х | Х | 1 732 311,00 | 232 310,99 | 1 500 000,01 |
Решение.
Способ 1.
K’ = K I = 4000 44=4044,
где K – капитал или заем, за использование которого заемщик выплачивает определенный процент;
I – процентный платеж или доход, получаемый кредитором от заемщика за пользование денежной ссудой;
P – процентная ставка, показывающая сколько д. е. должен заплатить заемщик за пользование 100 ед. капитала в определенном периоде времени (за год);
D – время, выраженное в днях.
360 – число дней в году.
Способ 2.
Время t = 80/360 = 2/9.
K’ = K K×i×t = 4000(1 0.05×2/9) = 4044,
Где i – процентная ставка, выраженная в долях единицы,
T – время, выраженное в годах.
Решение
2×K = I.
2×K = K×9×g/100,
G = 2×100/9 = 22.22
Постнумерандо по 5000 д. е. при 8% годовых, если капитализация осуществляется каждые полгода.
Решение:
При ежегодной капитализации: C0 = a×IVpn = 5000×IV8 = 5000×6.71=33550
Решение
Таблица – План погашения займа (амортизационный план)
Год | Долг | Процентный Платеж | Выплата Долга | Аннуитет |
1 | 20000 | 400 | 1826.53 | 2226.53 |
2 | 18173.47 | 363.47 | 1863.06 | |
3 | 16310.41 | 326.21 | 1900.32 |
Пояснения к таблице
Аннуитет вычисляем по формуле: a = K×Vpn = 20000×V2 = 20000×0.1113 = 2226.53 д. е.
Чтобы определить выплату задолженности b1, вычисляем величину процентного платежа I:
I1 = K1×p/100 = 20000×2/100 = 400 д. е.
Выплата задолженности представляет собой разницу между аннуитетом и процентным платежом:
B1 = a – I1 = 2226.53 – 400 = 1826.53 д. е.
Таким образом, после первого года долг сократится на 1826.53 д. е. Остаток долга равен:
K2 = 20000 – 1826.53 = 18173.47 д. е.
Вычислим процентный платеж на остаток долга:
I2 = 18173.47×2/100 = 363.47 д. е.
Вторая выплата составит:
B2 = a – I2 = 2226.53 – 363.47 = 1863.06 д. е.
Долг уменьшится на величину 1863.06, остаток долга составит:
K3 = 18173.47 – 1863.06 = 16310.41 д. е.
Далее
I3 = 16310.41×2/100 = 326.21 д. е.
Третья выплата задолженности составит:
B3 = a – I3 = 2226.53 – 326.21 = 1900.32 д. е.
Решение:
Используем формулу наращения для простых процентов:
где Р – первоначальная сумма ссуды;
i – ставка простых процентов;
P=20 тыс. руб.
I=0.5
1) точные проценты с точным числом дней ссуды (английская практика):
K=365 (дней) – количество дней в году;
t – количество дней, за которые начисляются проценты;
15 марта – порядковый номер в году – 74;
5 июля – порядковый номер в году – 186.
Точное число дней ссуды:
T=186-74=112 дней.
2) обыкновенные проценты с точным числом дней ссуды (французская практика):
K=365 (дней) – количество дней в году;
T=112 (дней) – количество дней, за которые начисляются проценты;
3) обыкновенные проценты с приближенным числом дней ссуды (германская практика):
K=365 (дней) – количество дней в году;
t – количество дней, за которые начисляются проценты;
Рассчитаем приближенное число дней ссуды t. Продолжительность ссуды определяется из условия, согласно которому месяц принимается за 30 дней:
15.03 – 30.03 – 16 дней;
апрель, май, июнь – по 30 дней;
1.07 – 5.07 – 5 дней.
T=16 30*3 5-1=110 дней.
Ответ: совокупный доход за период при начислении процентов по английской практике составит 20920 руб., при использовании французской практики начисления процентов – 20933 руб., а при начислении процентов по германской практике совокупный доход за данный период составит 20917 руб.





