Формула для анализа текущей стоимости инвестиций по ЧПС в Excel

Анализ текущей стоимости денег при разных суммах взносов и выплат

Допустим, что вместо разового инвестиционного взноса 300 000$ можно вложить только 150 000$ в первом году, 100 000$ – во втором и 50 000$ – в третьем году. Суммы, которые будут инвестированы уменьшаются в меру развития предприятия так как с каждым годом оно может позволить себе использовать большую сумму рефинансирования своих собственных средств.

Ниже на рисунке изображен график инвестиционных взносов на протяжении 3-х лет и выплаты дивидендов на протяжении остальных 4-х лет. Используется та же функция ЧПС, что и в предыдущем примере изменены только входящие значения и нет вычитания в формуле, так как в аргументах функции уже используются отрицательные числа:

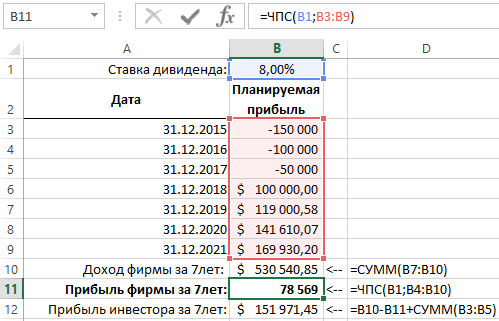
В первом примере инвестированная сумма не использовалась в вычислениях функции ЧПС. Просто итоговый результат вычисления сравнивался с объемом необходимых инвестиционных средств. В данном примере инвестированная сумма, разбитая на части и все они выражены отрицательными числами (расход), а суммы прибыли фирмы выражены положительными числами (приход).

В данном примере уже не сравнивается результат вычислений с объемом инвестиций, а сразу получаем итоговый результат через функцию ЧПС, поэтому нет смысла делать вычитание. Если в итоговом результате вычислений получаем число больше чем >0 – это значит, что серия прибыли фирмы, приносит больше чем >8% годовых.

Если же в результате было число меньше чем <0 – тогда доходность фирмы составляла меньше <8% годовых (чего не хватило бы даже чтобы рассчитаться с инвесторами). Как видно на рисунке данный инвестиционный план имеет положительный результат с точки зрения привлекательности для инвесторов, но значительно менее привлекательный для собственников фирмы.

Дисконтирование простыми словами

Рассмотрим пример

Банк сделал Васе персональное предложение по кредиту на сумму 200 тыс. руб. по ставке 10% годовых, сроком на год. Причем вернуть сумму с процентами можно всю сразу по завершении этого года.

Вася рассказал об этом своему другу Пете. И заметил, что все 200 тыс. руб. ему не нужны, но некоторой суммой он бы воспользовался. Петя предложил Васе взять весь кредит и ссудить часть суммы ему, а он, по прошествии года, вернет ее с такими же процентами.

Вася прикинул свои возможности и понял, что на возврат кредита он сможет набрать через год порядка 120 тыс. руб. Значит, вторую часть – еще 100 тысяч – должен к тому моменту вернуть Петя.

Сколько же нужно сегодня ссудить Пете под 10% годовых, чтобы через год он вернул 100 тысяч?

Считать нужно, исходя из формулы банковского (сложного) процента.

Например, общая сумма к возврату по Васиному кредиту:

S=200*(1 0,10)1 = 220

Степень 1 в формуле означает, что у кредита только один период выплаты – через год. Если бы срок был 2 года – в степень в формулу следовало бы поставить 2. И так далее.

Чтобы узнать, какая сумма, выданная под 10% годовых, через год превратиться в 220, нужно принять 200 тыс. руб. за Х и решить получившееся уравнение.

Х = 220/(1 0,10)1 = 200

А теперь Вася по той же методике посчитает, какая сумма превратится в 100 тыс. руб.

100/(1 0,10)1 = 90,91 тыс. руб.

Вася произвел дисконтирование и получил приведенную стоимость Петиной ссуды к возврату.

А мы запомним формулу дисконтирования:

   К

ПС = ————-

        (1 r) ^t

ПС – приведенная (дисконтированная) стоимость

К – дисконтируемая сумма

r – процентная ставка

t – период кредитования

Зачем берется банковская ставка

Снова приведем пример

Костя выиграл в лотерею. После уплаты налогов у него остался 1 миллион рублей. Костя решил открыть свой бизнес – небольшое кафе. Арендовал помещение, купил оборудование, нанял персонал, сам за всем следил, практически в своем кафе поселился… Через год получил первую чистую прибыль – 50 тысяч рублей.

В то время как на момент открытия кафе можно было положить деньги в банк на депозит по 6% годовых. И получить по окончании года доход в 60 тысяч рублей, миллион обратно в свое распоряжение и все это не особо напрягаясь и с минимальными рисками.

С этим примером мы вплотную подошли к тому, для кого в идеале делается бухгалтерская отчетность по МСФО. А делается она для потенциальных инвесторов, которые, посмотрев на нее, должны принять решение: вложить свои деньги в эту компанию или проще отнести их в банк на депозит?

То есть инвестор, анализируя состояние дел компании по отчетности, подготовленной по принципам МСФО, оценивает выбор между двумя инвестиционными проектами – с компанией и с банком.

А, поскольку, в бухотчетности мы отражаем то, что есть именно на текущий момент, то для информативного отражения, например, расчетов по аренде и лизингу, мы пользуемся вторым способом, позволяющим сравнить разные проекты – дисконтированием. И из этих же соображений часто подставляем в формулу ставку дисконтирования – величину банковского процента.

Зачем нужен показатель npv

Если у вас на примете есть перспективный бизнес-проект, в который вы готовы вложить деньги, советуем рассчитать его чистую приведенную стоимость.

Как рассчитать NPV проекта? Используйте такой порядок действий:

1. Оцените денежные потоки от проекта, то есть первоначальное вложение (отток) и ожидаемые поступления (притоки) денежных средств.
2. Определите стоимость капитала (cost of capital), так как этот показатель станет для вас ставкой дисконтирования.
3. Продисконтируйте притоки и оттоки от проекта по ставке, которую вам удалось рассчитать на предыдущем шаге.
4. Сложите все дисконтированные потоки – это и будет NPV проекта.

Далее можете принимать решение об инвестициях, но помните: в проект стоит вкладываться при NPV больше нуля, если же этот показатель ниже нуля, лучше отказаться от своей задумки.

На самом деле, все просто – если NPV равен нулю, значит, денежных потоков от проекта хватит, чтобы:

• возместить инвестированный капитал;
• обеспечить доход на этот капитал.

При положительном NPV проект принесет прибыль, и чем выше его уровень, тем выгоднее окажутся вложения в проект.

Кредиторы, то есть люди, дающие деньги в долг, имеют фиксированный доход, поэтому все средства, превышающие этот показатель, остаются акционерам. Если компания решает одобрить проект с нулевым NPV, акционеры сохранят свою позицию – компания станет больше, но акции не поднимутся в цене. При положительном NPV проекта акционеры станут богаче.

NPV позволяет рассчитать, какой из инвестиционных проектов выгоднее, когда их несколько, но компания не имеет средств на реализацию сразу всех. В этом случае приступают к проектам с наибольшей возможностью заработать или с самым высоким NPV.

Сегодня нужно просто рассчитать NPV, чтобы оценить выгодность инвестиционных проектов. Среди достоинств этого показателя аналитики называют:

• четкие критерии принятия решения об инвестировании – первоначальные инвестиции, выручка на каждом этапе, доходность альтернативных вложений;
• учет изменения стоимости денег с течением времени;
• учет рисков за счет использования различных ставок дисконтирования.

Но не стоит заблуждаться и считать этот показатель абсолютно точным коэффициентом. Нередко сложно корректно рассчитать ставку дисконтирования, особенно когда речь идет о многопрофильных проектах. Также отметим, что при расчете не учитывается вероятность исхода каждого проекта.

Значение ставки дисконтирования при расчёте npv

Как определить ставку дисконтирования

Отметим, что в случае с долгосрочной арендой или лизингом у сторон сделки будет немного разный подход к оценке.

Арендатор (или лизингополучатель) должен показать, что для него взять объект в аренду или лизинг выгоднее, чем взять кредит и купить такой же объект. (Ну, или не выгоднее, и тогда отражение по приведенной стоимости даст убыток). Поэтому арендатор в качестве ставки для подстановки в формулу дисконтирования берет ставку, по которой он мог бы взять кредит на приобретение аналогичного объекта.

Если у арендатора уже есть подобные кредиты – можно опираться на ставку по ним. Если нет – нужно определять по какой ставке арендатор, на дату получения объекта,  мог бы взять кредит с аналогичным сроком и обеспечением для приобретения примерно такого же.

Важно! В МСФО процесс выбора ставки дисконтирования гораздо более обусловлен и имеет несколько вариантов расчета. Причем выбранный вариант еще надо обосновать аудиторам. Российские ФСБУ, дублируя необходимость применения дисконтирования, пока не настолько усложнены и можно следовать общим предписаниям стандарта и логике.

У арендо- и лизингодателя ситуация больше похожа на ситуацию Кости, получившего миллион. У Кости заключен договор аренды, куплено оборудование и мебель. Как отбить обратно свой миллион, чтобы подумать, куда его дальше лучше вложить?

Продолжим пример

Костя нашел арендатора, который готов арендовать его кафе. Помещение, соответственно, пойдет в субаренду, а оборудование и мебель – в аренду от самого Кости. Договор заключен на 4 года, для упрощения расчетов примем, что арендатор рассчитывается сразу за год по 250 000 рублей. То есть, через 4 года Костя вернет свой миллион.

При этом у Кости уже есть вложения по объекту аренды:

480 000 – аренда (опять же, чтобы не перегружать пример, будем считать, что Костя оплатил всю сумму на 5 лет авансом);

280 000 – затраты на покупку оборудования и мебели;

40 000 – расходы на монтаж и обслуживание оборудования.

Итого можно определить стоимость инвестиционного вложения Кости – 800 тыс. руб.

То есть, следуя все тем же формулам, выполняется равенство:

800*(1 r)4 = 1 000 000

Вот эта ставка r, при которой валовая стоимость инвестиции в аренду (будущий 1 миллион) равна справедливой стоимости вложений арендодателя (800 тысяч) и будет ставкой дисконтирования, которая нужна арендодателю. Зависящей от условий конкретного договора и позволяющей сравнивать его с другими подобными договорами.

Для полноты картины следует учесть, что оборудование и мебель, которые вернутся к Косте по окончании срока аренды, возможно, еще будут иметь какую-то ценность. Например, их можно будет продать как б/у, но еще годные к использованию. Поэтому, на практике, нужно эту ценность, называемую негарантированной ликвидационной стоимостью, оценить и добавить в равенство, приплюсовав к поступлениям от аренды.

Допустим, Костя договорился по окончании срока аренды помещения продать оптом находящееся в нем к тому моменту имущество (мебель и оборудование) за 50 000 рублей.

Тогда равенство для вычисления ставки дисконтирования примет вид

800*(1 r)4 = 1 050 000 (1 000 000 50 000)

Отметим также, что на практике решить как уравнение подобное равенство для большого временного отрезка, а потом вычислить дисконтированные величины арендных платежей не так просто. Не всякий и не со всяким калькулятором справится. Поэтому далее мы поговорим о том, какие есть способы упростить расчеты.

Округление в финансовых формулах

При использовании финансовых формул проблема округления значений ощущается особенно остро. Excel предлагает несколько функций для выполнения этой задачи: ОКРУГЛ, ОКРУГЛВНИЗ И ОКРУГЛВВЕРХ. Чтобы предотвратить накопительные ошибки, округляйте только конечный получаемый результат.

Другими словами, избегайте округления промежуточных данных. Обычно результаты финансовых расчетов отображаются в виде чисел с двумя десятичными разрядами или вообще без таковых. В промежуточных расчетах это предполагает получение результатов с точностью до цента или доллара.

В отдельных случаях вычисления базируются на приблизительных данных или данных, полученных в результате эмпирического анализа или подбора параметров. Поэтому уже давно обычной практикой стало применение округленных значений (чтобы не утруждать себя вводом длинных значений).

Однако вы знаете, что арендная плата может изменяться (скажем, в диапазоне от 42 до 45 долларов). В результате конечная сумма аренды будет колебаться в небольших пределах. Чтобы избежать излишней неточности, конечную сумму можно округлить до ближайших ста или даже тысячи долларов.

Определение текущей стоимости в excel

Плюсы и недостатки

Универсальный метод расчёта приведённой стоимости был разработан экспертами для того, чтобы каждый человек имел возможность получения итоговой прибыли. Но, как и у любого другого финансового инструмента, у чистого приведённого NPV есть выгодные и негативные стороны.

К основным преимуществам можно отнести:

• Проводить корректировку объёма финпотоков и приведённой стоимости во времени можно за счёт учёта дисконтставки проекта.
• Действуют простые однозначные правила, помогающие со сложными решениями, которые касаются инвестпривлекательности идеи.
• Можно ввести учёт премии за рисковую составляющую в составе дисконтставки. Стоит отметить, что для высокорисковых проектов допустимо использовать повышенный процент.

Несмотря на все вышеперечисленные преимущества, у чистого приведённого NPV есть и негативные стороны. Каждый специалист должен помнить о ряде ограничений:

• Неопытному человеку сложно спрогнозировать будущие денежные потоки. Если пользователь решил разобраться в столь ответственном этапе работы, то все полученные им расчёты должны быть точными, так как от этого зависит итоговый объём приведённого NPV.
• Трудно оценить сложные инвестпроекты. Особые сложности возникают из-за многочисленных рисков, которых очень много в долгосрочном горизонте. Специалист должен скорректировать дисконтставки.
• Приведённый NPV может использоваться только для отображения абсолютного показателя дохода. Чтобы результаты анализа были достоверными, нужно дополнительно рассчитывать относительные показатели (внутренней нормы по доходности, инвестрентабельности).
• Стандартная форма приведённого NPV не корректируется на реинвест финансовых потоков.

Применение приведённой npv на практике

Универсальные формулы приведённой стоимости активно используют опытные и начинающие инвесторы. Такой подход помогает оценить целесообразность внесения финсредств. Эксперты рекомендуют использовать три варианта расчёта приведённой NPV:

1. Если чистая стоимость в приведённый период =0, это указание, что инвестиции окупаются, но сам вкладчик не получит никакой прибыли. К примеру: если гражданин использовал кредитные деньги, то поступающие финпотоки благоприятствуют расчёту с кредитором полностью. Инвестор сможет выплатить все начисленные %, а сам счёт останется неизменным. Здесь лучше найти иные варианты вклада, с более оптимистичным приведённым результатом чистой итоговой стоимости.
2. Когда при изучении приведённого показателя NPV было получено плюсовое значение стоимости, то инвестиция полностью окупается. А сама цифра отображает цифру прибыли вкладчика. Конечно, в этом случае инвестиции более чем оправданы, так как в итоге человек получает хорошую прибыль.
3. В редких случаях после многочисленных расчётов стоимости выходит отрицательное значение приведённой цифры. В такой ситуации инвестиции пользователя не окупаются, а сам вкладчик остаётся с убытками. Если исследуемый проект с минусовым значением, от работы с ним правильнее отказаться.

К инвестпроектам могут относиться только те бизнес-идеи, у которых преобладают положительные значения цифр. Когда вкладчик не может определиться, тогда предпочесть лучше вариант с наибольшим показателем чистого приведённого NPV.

Функция чиствндох

С помощью этого средства как раз можно вычислить ставку внутренней доходности для арендодателя (лизингодателя).

Чтобы воспользоваться данным инструментом, нужно внести в лист Excel данные по датам и платежам договора. А в первой строке отразить величину инвестиционных вложений со знаком «-».

Возьмем данные из примера про сдачу в аренду Костиного кафе. Пусть кафе он передал арендатору 01.01.2022, а платит арендатор по истечении года. Для упрощения не станем учитывать негарантированную ликвидационную стоимость.

Далее ставим курсор в свободную ячейку и нажимаем на значок формул. Формула ЧИСТВНДОХ находится в разделе Финансовые. В англоязычном Excel она же называется XIRR.

Вносим данные для расчета, выделяя нужные области. На первое место ставим суммовые значения, на второе – даты

Далее жмем ОК и получаем ставку дисконтирования, с помощью которой арендодателю надо производить вычисления для отражения в отчетности договоров по ФСБУ 25/2022.

Важно!

Переписывать по датам обязательно нужно все платежи по условиям договора. Если у вас, к примеру, договор заключен на 5 лет с платежами ежемесячно, то придется заполнить 60 строк под каждый платеж.

А вот такие параметры как периодичность, аннуитетность – на точность вычислений не влияют. С помощью формулы можно рассчитывать ставку внутренней доходности и в случае, если платежи идут произвольно, и в случае, если их суммы не равные.

Функция чистнз

С помощью этой формулы, зная ставку дисконтирования, можно быстро вычислить чистую стоимость инвестиций в аренду на дату отражения в отчетности. Английская аббревиатура функции XNPV. Эта формула тоже больше подойдет для арендодателя (лизингодателя).

Для вычислений можно завести еще один столбец в табличке, которая получилась из платежей и их дат.

На момент передачи стоимость инвестиций принимаем равной справедливой стоимости вложений в объект аренды или лизинг. Скажем по секрету, что если объект ОС, передаваемый в аренду, учитывался с соблюдением правил приема на баланс, оценки и тестирования на обесценение, то его стоимость при  передаче вполне можно считать справедливой.

А далее начинаем вычислять чистую стоимость инвестиций для каждого последнего дня года.

Важно! Если на дату, на которую определяется приведенная чистая стоимость инвестиций, приходится и дата платежа по договору, то сумму платежа нужно вычесть из значения, получившегося по формуле ЧИСТНЗ.

Выбираем значения, начиная от того, на дату которого считаем и далее до конца договора. Даты выбираем соответственно.

Вычитаем из получившегося по формуле значения сумму платежа по договору, чтобы получить справедливое значение на конец дня 31 декабря.

При наступлении следующей даты поступаем так же. Расчеты рекомендуется сохранить для каждого договора.