Методы оценки эффективности реальных инвестиций на основе расчета чистого приведенного дохода
Методика определения чистого приведенного дохода NPV (Net Present Value) заключается в суммировании дисконтированных сальдо потоков реальных денег в течение расчетного периода времени.
Определяя коэффициент дисконтирования, обычно исходят из гарантированного уровня доходности финансовых инвестиций, который обеспечивается государственным банком по вкладам или при операциях с ценными бумагами. При этом часто предусматривается надбавка за риск, причем, чем рискованнее проект, тем больше размер надбавки. Т.о. процентная ставка, используемая в качестве коэффициента дисконтирования имеет вид: r = i rр, где i – безрисковая доходность (процентная ставка по банковским депозитам или ставка доходности государственных облигаций), rp – надбавка за риск.
Рассматриваемый проект может быть признан эффективным, если чистый приведенный доход положителен (NPV >0), значит проект доходный. При сравнении вариантов осуществления инвестиционных проектов одинаковой продолжительности следует руководствоваться критерием максимума чистого приведенного дохода (NPV→max). Если рассматриваемые варианты различаются продолжительностью расчетного периода, то в качестве ключевого оценочного показателя используется среднегодовой чистый приведенный доход. Следовательно, и выбор наилучшего варианта осуществляется по критерию максимума среднегодового значения NPV.
При однократном инвестировании для оценки NPV производится сопоставление величины исходной инвестиции (IС) с общей суммой дисконтированных чистых денежных поступлений в течение прогнозируемого срока. Приток денежных средств осуществляется в различные моменты времени. В соответствие с этим он дисконтируется с помощью коэффициента r, устанавливаемого аналитиком (инвестором) самостоятельно, исходя из ежегодного процента возврата, который он хочет или может иметь на инвестируемый им капитал. Допустим, прогнозируется, что в результате инвестирования средств в объем IC в течение n лет будут поступать годовые доходы в размере 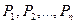 . Общая накопленная величина дисконтированных доходов в этом случае определяется по формуле:
. Общая накопленная величина дисконтированных доходов в этом случае определяется по формуле:
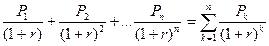 ,
,
Тогда чистый приведенный доход равен:
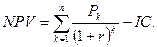
Очевидно, что если NPV>0, то проект прибыльный, его следует принять, если NPV<0, то проект убыточный, его следует отвергнуть, если NPV=0, то проект ни прибыльный, ни убыточный.
Пример. Требуется проанализировать проект со следующими характеристиками по годам: – 150;30;70; 70;30 млн. рублей. Требуемая норма доходности по проекту 12%.
Решение: 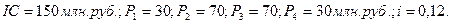
Определим чистый приведенный доход:
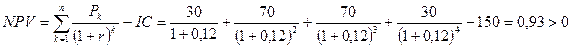
Поскольку чистый приведенный доход положителен (составляет 930 тысяч рублей), то проект принимается, так как является прибыльным.
Если предполагается не разовое инвестирование финансовых ресурсов, а последовательное в течение m лет в объемах 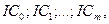 то формула для вычисления NPV будет иметь вид:
то формула для вычисления NPV будет иметь вид:
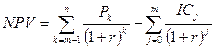
Пример.Мясокомбинат планирует приобрести новое оборудование. Для этого необходимо подготовить соответствующее помещение. Подготовка займет несколько месяцев. Подготовительные затраты составят 500 тыс. рублей. Оборудование стоимостью 3 млн. рублей, планируют приобрести в конце первого года и затем эксплуатировать в течение 3 лет. Денежный доход от эксплуатации этого оборудования за этот период по годам составит 1млн. руб.; 1,5 млн. руб. и 2 млн. руб. соответственно. Оцените этот инвестиционный проект, если требуемый уровень доходности составляет 10%.
Решение: Затраты на подготовку помещения могут рассматриваться как прединвестиционные затраты в 0-вом году.
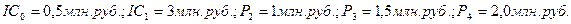
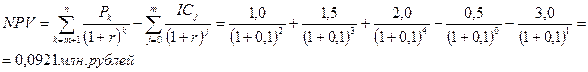
Поскольку NPV= 92,1 тыс. руб. >0, то проект прибыльный.
В случае если в результате инвестирования определенных средств возникает регулярный финансовый поток (финансовая рента), то для оценки NPV можно использовать теорию финансовых рент.
Пример. Некая фирма собирается за 55 млн. рублей прибрести помещение для магазина. Предполагается, что организация продаж в этом магазине обеспечит приток денежных средств в размере 10 млн. рублей на протяжении 10 предстоящих лет. Стандартный уровень доходности по альтернативным формам инвестирования составляет 9,5%. Решите вопрос о целесообразности приобретения магазина.
Решение: 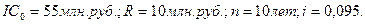
В результате инвестирования средств в размере 55 млн. рублей образовалась финансовая рента длительностью 10 лет с членом, равным 10 млн. рублей. Найдем современную стоимость этой ренты.
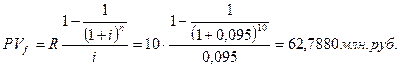
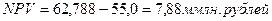 .
.
Поскольку NPV  > 0, то целесообразно приобрести помещение.
> 0, то целесообразно приобрести помещение.
§
Индекс рентабельности инвестиций – это отношение суммарного дисконтированного сальдо денежного потока, определённого без учёта инвестиций по проекту, к суммарным дисконтированным инвестициям.
В простейшем случае, когда в результате инвестирования средств в размере IС возникает денежный поток 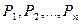 , индекс рентабельности инвестиций рассчитывается по формуле:
, индекс рентабельности инвестиций рассчитывается по формуле:
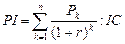
При неоднократном инвестировании эта формула приобретает вид:
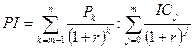 .
.
В отличие от чистого приведённого дохода индекс рентабельности является относительным показателем. Он характеризует уровень доходов на единицу затрат, т.е. эффективность вложений.
Очевидно, что, если PI >1 , то проект следует принять. Если PI<1, то проект следует отвергнуть. Если PI=1, то проект не является ни прибыльным, ни убыточным.
Чем больше значение индекса рентабельности, тем выше отдача от каждого рубля, инвестированного в данный проект, благодаря чему критерий PI очень удобен при выборе одного проекта из нескольких альтернативных, имеющих примерно одинаковые значения NPV, но разные объёмы требуемых инвестиций. Из этих проектов выгоднее тот, который обеспечит большую эффективность вложений.
Пример.Предприятие закупило новую технологическую линию за 1000 тыс. руб. Срок эксплуатации оборудования 6 лет. Денежный доход от использования оборудования по годам составит 250; 300; 350; 400; 450; 500 тыс. руб. соответственно. Рассчитать индекс рентабельности, если норма дисконта составляет 20%.
Решение: 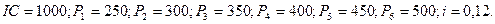
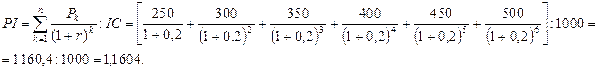
Поскольку индекс рентабельности PI= 1,1604>1, то проект следует принять.
§
Срок окупаемости (период возмещения) – это минимальный период времени, в течение которого чистый дисконтированный доход становится положительным. Этот показатель характеризует период времени, в течение которого сделанные инвестором вложения в проект возместится доходами от его реализации.
Формула для расчета дисконтированного срока окупаемости:
DРР=min n, при котором выполняется неравенство: 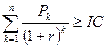
Применяются следующие подходы к оценке инвестиционных проектов по критерию срока окупаемости:
а) проект принимается, если окупаемость имеет место;
б) проект принимается только в случае, если срок окупаемости не превышает установленного в компании лимита (например, 5 лет).
Пример. Рассчитайте дисконтированный срок окупаемости инвестиционного проекта, характеризующегося по годам следующим денежным потоком:
-250; 100; 150; 160; 100 тысяч рублей. Норма дисконта 11%.
Решение:
Вычисления удобно свести в расчетную таблицу:
(тыс. рублей)
| Годы | Денежный поток | Дисконтный множитель | Дисконтирован-ный денежный поток | Дисконтирован-ный денежный поток нарастаю-щим итогом |
| – 250 | 1,000 | – 250,00 | – 250,00 | |
| 0,901 | 90,10 | – 159,90 | ||
| 0,812. | 121,80 | – 38,10 | ||
| 0,731 | 116,96 | 78,86>0 | ||
| 0,659 | 65,90 |
Как видим, инвестиционный проект полностью окупится в течение трех лет.
Для того, чтобы определить более точное значение DРР, разделим последнее из отрицательных значений в последнем столбце таблицы на следующее за ним число в предпоследнем столбце: 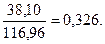
Таким образом, DРР= 2, 326 года или 2 года и 119 дней.
§
Внутренняя норма доходности IRR (international rate of return) – показатель, широко используемый при оценке эффективности инвестиционных проектов.
Реализация любого инвестиционного проекта требует привлечения финансовых ресурсов, за которые необходимо платить. Так за заемные средства платят проценты, за привлеченный акционерный капитал -дивиденды и т.д.
Показатель, характеризующий относительный уровень этих расходов, является ценой за использованный (авансируемый) капитал. При финансировании проекта из различных источников этот показатель определяется по формуле средней арифметической взвешенной.
Чтобы обеспечить доход от инвестированных средств или, по крайней мере, их окупаемость, необходимо добиться такого положения, когда чистая текущая стоимость будет больше нуля или равна нулю.
Для этого необходимо подобрать такую процентную ставку дисконтирования членов потока платежей, которая обеспечит получение неотрицательного чистого приведенного дохода (NPV 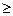 0).
0).
Такая ставка должна отражать ожидаемый усредненный уровень ссудного процента на финансовом рынке с учетом фактора риска.
Поэтому под внутренней нормой доходности понимают ставку дисконтирования, использование которой обеспечивает равенство текущей стоимости денежных оттоков и текущей стоимости ожидаемых денежных притоков, т.е. при начислении на сумму инвестиций процентов по ставке, равной внутренней норме доходности, обеспечивается получение распределенного по времени дохода.
Показатель внутренней нормы доходности – IRR характеризует максимально допустимый относительный уровень расходов, которые могут быть произведены при реализации данного проекта.
Например, если для реализации проекта получена банковская ссуда, то значение IRR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которой делает проект убыточным.
Таким образом, смысл этого показателя заключается в том, что инвестор должен сравнить полученное значение IRR с ценой привлеченных финансовых ресурсов (cost of capital – CC).
Если IRR>СС, то проект следует принять;
IRR<СС – проект следует отвергнуть;
IRR=СС – проект ни прибыльный, ни убыточный.
Практическое применение данного метода сводится к последовательной итерации, с помощью которой находится дисконтирующий множитель, обеспечивающий равенство NPV=0.
При этом алгоритм решения следующий.
Ориентируясь на существующие в момент анализа процентные ставки на ссудный капитал, выбирают два значения коэффициента дисконтирования 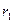 <
< 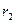 таким образом, чтобы в интервале [
таким образом, чтобы в интервале [ 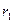 ,
, 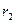 ] функция
] функция 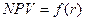 меняла свое значение с « » на «− » или наоборот. Затем используют формулу:
меняла свое значение с « » на «− » или наоборот. Затем используют формулу:
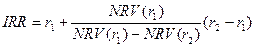 ,
,
где 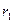 – значение процентной ставки в дисконтном множителе, при котором
– значение процентной ставки в дисконтном множителе, при котором 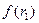 >0
>0 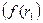 <0);
<0);
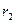 – значение процентной ставки в дисконтном множителе, при котором
– значение процентной ставки в дисконтном множителе, при котором 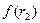 <0
<0 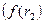 >0).
>0).
Точность вычислений обратно пропорциональна длине интервала [ 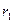 ,
, 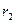 ]. Наиболее точный результат достигается в случае, когда длина интервала минимальна, т.е. когда
]. Наиболее точный результат достигается в случае, когда длина интервала минимальна, т.е. когда 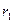 и
и 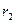 – ближайшие друг к другу значения коэффициента дисконтирования, в случае изменения знака NPV с « » на «-» удовлетворяющие условиям:
– ближайшие друг к другу значения коэффициента дисконтирования, в случае изменения знака NPV с « » на «-» удовлетворяющие условиям:
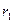 – значение коэффициента дисконтирования, минимизирующее положительное значение NPV,т.е.
– значение коэффициента дисконтирования, минимизирующее положительное значение NPV,т.е. 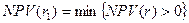 ;
;
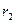 – значение коэффициента дисконтирования, максимизирующие отрицательное значение показателя NPV, т.е.
– значение коэффициента дисконтирования, максимизирующие отрицательное значение показателя NPV, т.е. 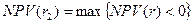 в случае изменения знака NPV с « » на «-»).
в случае изменения знака NPV с « » на «-»).
Подобным же образом описывается ситуация для случая когда функция меняет знак с «−» на « ».
Пример. Определить значение внутренней нормы доходности IRR для проекта, рассчитанного на 3 года, требующего инвестиции в размере 20 млн. руб. и имеющего предполагаемые денежные поступления в размере 6 млн. руб.(первый-год), 8 млн.руб. (второй год) и 14 млн.руб. (третий год).
Решение:
Возьмем два произвольных значения процентной ставки для коэффициента дисконтирования 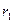 =15% и
=15% и 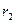 =20%.
=20%.
Соответствующие расчеты сведем в таблицу:
| Год | Денежный поток | Расчет I | Расчет II | ||
Дисконтный множитель для 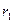 =15% =15% | 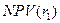 | Дисконтный множитель для 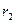 =20% =20% | 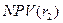 | ||
| 0-й | −20,0 | 1,0 | −20,0 | 1,0 | −20,0 |
| 1-й | 6,0 | 0,8696 | 5,2176 | 0,8333 | 4,9998 |
| 2-й | 8,0 | 0,7561 | 6,0488 | 0,6944 | 5,5552 |
| 3-й | 14,0 | 0,6575 | 9,2050 | 0,5787 | 8,1018 |
| Σ | 0,4714 | −1,3432 |
Для расчета IRR применим формулу:
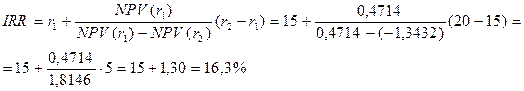
Уточним величину ставки. Для этого примем значения процентных ставок, равными 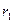 =16% и
=16% и 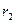 =17% , т.к. 16,3
=17% , т.к. 16,3 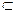 (16, 17).
(16, 17).
Произведем новый расчет.
| Год | Денежный поток | Расчет I | Расчет II | ||
Дисконтный множитель для 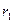 =16% =16% | 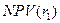 | Дисконтный множитель для 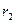 =17% =17% | 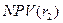 | ||
| 0-й | −20,0 | 1,0 | −20,0 | 1,0 | −20,0 |
| 1-й | 6,0 | 0,8662 | 5,1972 | 0,8547 | 5,1282 |
| 2-й | 8,0 | 0,7432 | 5,9200 | 0,7305 | 5,8440 |
| 3-й | 14,0 | 0,6407 | 8,9698 | 0,6244 | 8,7416 |
| Σ | 0,0870 | −0,2862 |
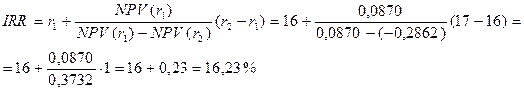
Таким образом, IRR=16,23 является верхним пределом процентной ставки, по которой фирма может окупить кредит для финансирования инвестиционного проекта. Для получения прибыли фирма должна брать кредит по ставке менее 16,23%.
§
Ценные бумаги классифицируются по ряду признаков. Подробно классификация ценных бумаг рассматривается в курсе «Рынок ценных бумаг». Мы остановимся на наиболее существенных для проведения инвестиционного анализа признаках: функциональное назначение; срок обращения и доход по ценным бумагам.
По функциональному назначению ценные бумаги подразделяются на долговые и долевые ценные бумаги и платежные документы.
К долговым ценным бумагам относятся облигации, депозитные и сберегательные сертификаты, банковские книжки на предъявителя.
К долевым ценным бумагам относятся акции.
К платежным документам относятся векселя и чеки.
Обращение ценных бумаг всегда ограничено временными рамками. Существуют ценные бумаги со сроком обращения до одного года, так называемые краткосрочные ценные бумаги. Ценные бумаги, которые имеют срок обращения от одного до пяти лет, называются среднесрочными, а более пяти лет – долгосрочными.
Доходом по ценным бумагам могут быть процентные выплаты в денежной форме, в виде купонных выплат, дивидендов. Все зависит от того, каков порядок погашения, выплаты дохода, и в какой форме доход заложен в условиях выпуска, обращения и погашения ценных бумаг. Согласно этому признаку классификации ценные бумаги можно представить как процентные с постоянным и переменным доходом, купонные, дисконтные, выигрышные и дивидендные.
Рассмотрим, что представляют собой такие виды ценных бумаг, как облигации, акции и векселя.
Облигация – это кредитная ценная бумага, удостоверяющая внесение средств ее владельцем и подтверждающая право владельца требовать ее погашения (выплату номинальной стоимости или номинальной стоимости и процентов) в установленные сроки. При этом условия и сроки погашения (в том числе досрочного) оговариваются в решении о выпуске облигаций.
Доход по облигациям может быть представлен, как разница между ценой покупки и ценой продажи (погашения). Такой вид дохода называется дисконтным. Кроме того, доход может быть в виде процентного (купонного) дохода.
Акции – ценные бумаги, выпускаемые акционерным обществом, свидетельствующие о вложении их владельцами определенной суммы денег в капитал акционерного общества и дающие право получать ежегодный доход – дивиденд. Дивиденды выплачиваются из чистой прибыли общества.
Акции бывают привилегированные и обыкновенные. Владельцы привилегированных акций получают дивиденды обычно в виде не зависящего от размера прибыли процента, Владельцы обыкновенных акций получают часть прибыли, которая остается после оплаты привилегированных акций. Обыкновенные акции дают возможность участвовать в управлении акционерным обществом и получать интересующую акционера информацию. (Облигации такого права не дают). Владельцы привилегированных акций не имеют права голоса.
Вексель представляет собой разновидность письменного долгового обязательства векселедателя оплатить сумму, указанную на векселе, его владельцу (векселедержателю) при наступлении срока платежа или по его предъявлении.
Инвестор, принимая решение о целесообразности приобретения той или иной ценной бумаги, пытается оценить экономическую эффективность планируемой операции. При этом он ориентируется на абсолютные или на относительные показатели. В первом случае речь может идти о цене или стоимости актива, во втором — о его доходности.
Логика рассуждений инвестора в первом случае такова. Ценная бумага имеет две взаимосвязанные абсолютные характеристики: объявленную текущую рыночную цену ( 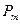 ), по которой ее можно приобрести на фондовом рынке, и теоретическую, или внутреннюю, стоимость (
), по которой ее можно приобрести на фондовом рынке, и теоретическую, или внутреннюю, стоимость ( 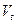 ).
).
Обе характеристики динамично меняются во времени, и с позиции конкретного инвестора часто не совпадают. Дело в том, что по сравнению с ценой, которая реально существует и объективна, поскольку она объявлена и ценная бумага по ней равнодоступна любому участнику рынка, внутренняя стоимость гораздо более неопределенна и субъективна. Под субъективностью в данном случае понимается то обстоятельство, что каждый инвестор имеет свой взгляд на внутреннюю стоимость актива, полагаясь в ее оценке на результаты собственного субъективного анализа.
Любая ценная бумага имеет внутренне присущую ей ценность, которая может быть количественно оценена как дисконтированная стоимость будущих поступлений, генерируемых этой бумагой, т.е. при ее оценке нужно двигаться от будущего к настоящему. Все дело лишь в том, насколько точно удается предсказать эти поступления, анализируя общую ситуацию на рынке, инвестиционную и дивидендную политику компании, инвестиционные возможности и т.п. Текущая внутренняя стоимость ( 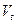 ) любой ценной бумаги в общем виде может быть рассчитана по формуле:
) любой ценной бумаги в общем виде может быть рассчитана по формуле: 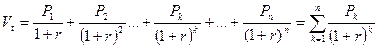 ,
,
Где 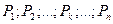 – предполагаемые поступления, r – требуемая данным инвестором норма прибыли, n – период финансовой операции.
– предполагаемые поступления, r – требуемая данным инвестором норма прибыли, n – период финансовой операции.
Подставляя в эту формулу значения предполагаемых поступлений, требуемую норму доходности и продолжительность периода прогнозирования, можно рассчитать текущую внутреннюю стоимость любого финансового актива. Именно такой подход чаще всего и используется потенциальными инвесторами.
Как видно из формулы оценка теоретической стоимости зависит от трех параметров: ожидаемые денежные поступления, горизонт прогнозирования и норма прибыли, причем последний параметр, вероятно, наиболее существен. Дело в том, что первые два параметра тесно привязаны непосредственно к базисному активу и потому обладают большей степенью объективности. Приемлемая норма прибыли, закладываемая инвестором в анализ, в этом случае в принципе не имеет отношения к базисному активу – она лишь отражает доходность альтернативных вариантов вложения капитала, доступных возможно лишь данному инвестору, что и предопределяет выбор этого параметра. Вот почему именно нормой прибыли обычно варьируют инвесторы в процессе имитационного моделирования. В частности, приемлемая норма прибыли может устанавливаться инвестором такими же способами, как и при определении процентной ставки в множителе дисконтирования: 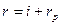 , где
, где 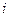 – безрисковая доходность (процентная ставка по банковским депозитам или ставка доходности государственных облигаций),
– безрисковая доходность (процентная ставка по банковским депозитам или ставка доходности государственных облигаций), 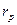 – надбавка за риск.
– надбавка за риск.
В качестве относительной оценки финансового актива может служить один из показателей, измеряющих доходность:
а) обычная годовая ставка процентов, рассчитанная по формуле: 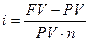 ,
,
б) сложная годовая ставка процентов:
Оценка облигаций
По способам выплаты дохода различают облигации с фиксированной или плавающей купонной ставкой и облигации с нулевым купоном. Для облигации с нулевым купоном эмиссионный курс устанавливается ниже номинального. Разница между ценой приобретения облигации и ценой ее погашения представляет собой доход инвестора. Периодическая выплата процентов по купонным облигациям осуществляется по купонам — вырезным талонам с напечатанной на нем цифрой купонной ставки. Периодичность выплаты процента по облигации определяется условиями займа. Она может быть квартальной, полугодовой или годовой. При прочих равных условиях, чем чаще начисляется доход, тем облигация выгоднее, тем выше ее рыночная цена.
Облигации могут быть охарактеризованы различными стоимостными показателями, основными из которых являются нарицательная (или номинальная), а также выкупная и рыночная цены. Нарицательная стоимость напечатана на самой облигации и используется чаще всего в качестве базы для начисления процентов. Этот показатель имеет значение только в двух случаях: в момент выпуска облигации при установлении цены размещения, а также в моменты начисления процентов, если они привязаны к номиналу. В период размещения облигационного займа цена облигации, как правило, совпадает с ее нарицательной стоимостью.
Выкупная цена (синонимы: цена досрочного погашения, отзывная цена) — это цена, по которой производится выкуп облигации эмитентом по истечении срока облигационного займа или до этого момента, если такая возможность предусмотрена условиями займа. Эта цена совпадает с нарицательной стоимостью, как правило, в том случае, если заем не предполагает досрочного его погашения.
Рыночная (курсовая) цена облигации определяется конъюнктурой рынка. Значение рыночной цены облигации 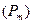 в процентах к номиналу (
в процентах к номиналу ( 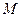 ) называется курсом облигации. Как уже отмечалось выше, эта цена может не совпадать с текущей внутренней стоимостью облигации.
) называется курсом облигации. Как уже отмечалось выше, эта цена может не совпадать с текущей внутренней стоимостью облигации.
Курс облигации определяется из выражения 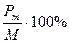
Пример. Облигация номиналом 500 руб. продается по
цене 465 руб., определите ее курс.
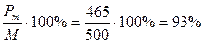 .
.
§
Поскольку денежные поступления по годам, за исключением последнего года, равны нулю, формула 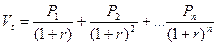 принимает вид:
принимает вид:
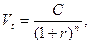
где 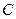 — сумма, выплачиваемая при погашении облигации;
— сумма, выплачиваемая при погашении облигации;
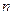 — число лет, через которое произойдет погашение облигации.
— число лет, через которое произойдет погашение облигации.
Пример.Облигации с нулевым купоном нарицательной стоимостью 1000 руб. и сроком погашения через пять лет продаются за 560,35 руб. Проанализировать целесообразность приобретения этих облигаций, если имеется возможность альтернативного инвестирования с нормой прибыли 14%.
Решение:
Анализ можно выполнять разными способами.
1 способ. 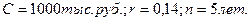
Рассчитать теоретическую стоимость облигации и сравнить ее с текущей ценой:
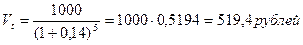 .
.
Расчет показывает, что приобретение облигаций является невыгодным вложением капитала, поскольку стоимость каждой облигации с позиции инвестора (519,4 руб.) меньше, чем цена, по которой продается облигация (560,35 руб.).
2 способ. Исчислить доходность данной облигации в виде эффективной годовой процентной ставки, если 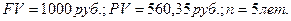
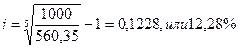
Поскольку доходность данных облигаций (12,28%) меньше альтернативной (14%), то их приобретение нецелесообразно.
§
Денежный поток при оценке облигаций фиксированной купонной ставкой (с постоянным доходом) складывается из одинаковых по годам поступлений А и нарицательной стоимости облигации М, выплачиваемой в момент погашения. Так как поступления по купонам образуют постоянную ренту постнумерандо с членом, равным А, то теоретическая стоимость облигации определяется по формуле:
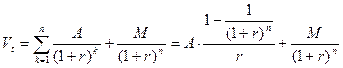
Пример.Номинал облигации, до погашения которой остается пять лет, равен 1000 руб., купон 10% выплачивается один раз в год. Определить цену облигации, чтобы она обеспечила покупателю доходность до погашения в размере 15% годовых.
Решение: 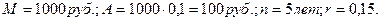
Так как в конце каждого года инвестор будет получать 100 руб., то теоретическая стоимость облигации составит:
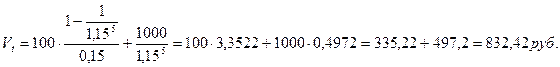
Курсовая цена облигации при этом равняется: 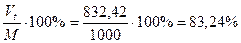
Полученный результат можно интерпретировать следующим образом: начисление сложных процентов по ставке 15% годовых на цену облигации (832,42 руб.) равноценно выплатам купонного дохода (ежегодно по 100 руб.) и суммы (1000 руб.) для погашения облигации в конце срока.
§
Акция представляет собой долевую ценную бумагу, свидетельствующую об участии ее владельца в собственном капитале компании. Обыкновенная акция дает право на получение плавающего дохода, т.е. дохода, зависящего от результатов деятельности общества, а также право на участие в управлении (одна акция — один голос).
Владелец привилегированной акции, как правило, имеет преимущественное право по сравнению с владельцем обыкновенной акции на получение дивидендов, в форме гарантированного фиксированного процента, а также на долю в остатке активов при ликвидации общества. Дивиденды по таким акциям в большинстве случаев должны выплачиваться независимо от результатов деятельности общества и до их распределения между держателями обыкновенных акций. Таким образом, привилегированные акции являются менее рискованными вложениями средств, однако это отражается на величине дивидендов, уровень которых в среднем, как правило, более низок по сравнению с уровнем дивидендов, выплачиваемых по обыкновенным акциям. Кроме того, привилегированная акция не дает право на участие в управлении обществом, если иное не предусмотрено уставными документами.
Стоимость акции, указанная на ее бланке называется номинальной стоимостью акции.
Внутренняя стоимость представляет собой расчетный показатель, который исчисляется по формуле: 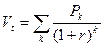 , где
, где 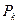 – ожидаемое денежное поступление в k-м периоде; r – приемлемая доходность.
– ожидаемое денежное поступление в k-м периоде; r – приемлемая доходность.
Эмиссионная цена представляет собой цену, по которой акция эмитируется, т.е. продается на первичном рынке. Эта цена может отличаться от номинальной стоимости.
Для учета и анализа наибольшее значение имеет курсовая (текущая рыночная) цена. Именно по этой цене акция котируется (оценивается) на вторичном рынке ценных бумаг. Курсовая цена зависит от разных факторов: конъюнктура рынка, рыночная норма прибыли, величина и динамика дивиденда, выплачиваемого по акции, и др. Она может определяться различными способами, однако в основе их лежит один и тот же принцип: сопоставление дохода, приносимого данной акцией, с рыночной нормой прибыли. В качестве показателя дохода можно использовать либо дивиденд, либо величину чистой прибыли, приходящейся на акцию.
Оценка целесообразности приобретения акций, как и в случае с облигациями, предполагает расчет теоретической стоимости акции и сравнения ее с текущей рыночной ценой.
Привилегированные акции, как и бессрочные облигации, генерируют доход 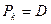 , где D – дивиденд, неопределенно долго, поэтому их текущая теоретическая стоимость определяется по формуле современной стоимости вечной ренты:
, где D – дивиденд, неопределенно долго, поэтому их текущая теоретическая стоимость определяется по формуле современной стоимости вечной ренты: 
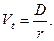 Таким образом, наиболее простым вариантом оценки привилегированной акции является отношение величины дивиденда к рыночной норме прибыли по акциям данного класса риска (например, ставке банковского процента по депозитам с поправкой на риск).
Таким образом, наиболее простым вариантом оценки привилегированной акции является отношение величины дивиденда к рыночной норме прибыли по акциям данного класса риска (например, ставке банковского процента по депозитам с поправкой на риск).
§
Наиболее распространенным методом оценки акций является метод, основанный на оценке их будущих поступлений, т.е. на применении формулы 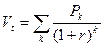 . В зависимости от предполагаемой динамики дивидендов конкретное представление этой формулы меняется. Базовыми являются три варианта динамики прогнозных значений дивидендов:
. В зависимости от предполагаемой динамики дивидендов конкретное представление этой формулы меняется. Базовыми являются три варианта динамики прогнозных значений дивидендов:
• дивиденды не меняются;
• дивиденды возрастают с постоянным темпом прироста;
• дивиденды возрастают с изменяющимся темпом прироста.
Вариант с неизменными дивидендами аналогичен ситуации с привилегированными акциями, т.е. применяется формула 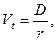 где D – размер дивиденда, r – требуемая норма прибыли. Если выплачиваются одинаковые дивиденды в течение всего времени, темп прироста дивидендов равен нулю и соответствующая модель называется моделью нулевого роста.
где D – размер дивиденда, r – требуемая норма прибыли. Если выплачиваются одинаковые дивиденды в течение всего времени, темп прироста дивидендов равен нулю и соответствующая модель называется моделью нулевого роста.
Пример.Компания гарантирует выплату дивидендов в размере 6 тыс. руб. на акцию в конце каждого года в течение неопределенно долгого времени. Имеет ли смысл покупать акции этой компании по цене 35 тыс. руб., если можно поместить деньги на депозит под 15% годовых?
Решение: 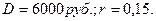
Из формулы 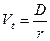 следует, что истинная стоимость акции составляет
следует, что истинная стоимость акции составляет 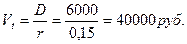 , следовательно, целесообразно приобрести акции по предлагаемой цене 35 тыс. руб.
, следовательно, целесообразно приобрести акции по предлагаемой цене 35 тыс. руб.
Вариант с постоянными темпами роста дивидендов. В этом случае предполагается, что выплачиваемые дивиденды растут от периода к периоду в одной пропорции. Соответствующая модель называется моделью постоянного роста.
Пусть базовая величина дивиденда (т.е. последнего выплаченного дивиденда) равна 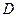 . Ожидается, что дивиденды будут ежегодно увеличиваться с темпом прироста
. Ожидается, что дивиденды будут ежегодно увеличиваться с темпом прироста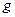 . Тогда по окончании первого года периода прогнозирования будет выплачен дивиденд в размере
. Тогда по окончании первого года периода прогнозирования будет выплачен дивиденд в размере 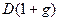 , по окончании второго года –
, по окончании второго года – 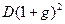 , по окончании k-го года – в размере
, по окончании k-го года – в размере 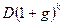 и т.д. Тогда формула
и т.д. Тогда формула 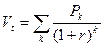 примет вид:
примет вид:
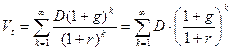
Последнее выражение представляет собой геометрическую прогрессию с первым членом 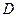 и знаменателем
и знаменателем 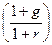 . Как известно, при
. Как известно, при 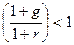 , т. е. при
, т. е. при 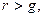 ее сумма может быть найдена по формуле:
ее сумма может быть найдена по формуле: 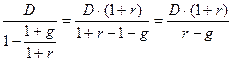 .
.
Следовательно, 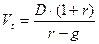 .
.
Данная формула называется моделью Гордона и имеет смысл при 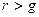 . Очевидно, что числитель формулы этой представляет собой первый ожидаемый дивиденд фазы постоянно роста.
. Очевидно, что числитель формулы этой представляет собой первый ожидаемый дивиденд фазы постоянно роста.
Пример.Компания за прошедший год выплатила 2,7 тыс. руб. на акцию. Согласно прогнозам дивиденды по акциям этой компании будут расти на 4% ежегодно в течение неопределенно долгого времени. Сделать вывод о целесообразности покупки акций компании по цене 20 тыс. руб., если можно поместить деньги на депозит под 14% годовых.
Решение: 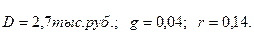 ,
,
Определим теоретическую стоимость акции:
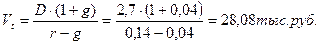
Так как стоимость акции с позиции инвестора превышает ее цену 20 тыс. руб., то имеет смысл приобрести акцию.
Вариант с изменяющимися темпами прироста дивидендов. При оценке акций, дивиденды которых возрастают с изменяющимся темпом прироста, используется модель переменного роста.
а) Предположим, что инвестор прогнозирует, что с высокой вероятностью наступит такой период S, после которого дивиденды будут расти с постоянным темпом 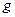 . До наступления S-го периода инвестор прогнозирует величину дивидендов по годам в размере:
. До наступления S-го периода инвестор прогнозирует величину дивидендов по годам в размере: 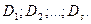
В этом случае теоретическая стоимость акции определяется по формуле:
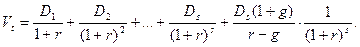
Пример.В течение последующих четырех лет компания планирует выплачивать дивиденды соответственно по 1,2; 1,8; 2; 2,4 долл. на акцию. Ожидается, что в дальнейшем дивиденд будет увеличиваться равномерно с темпом 5% в год. Рассчитайте теоретическую стоимость акции, если рыночная норма прибыли составляет 14%.
Решение: 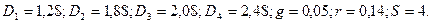
Теоретическая стоимость акции:
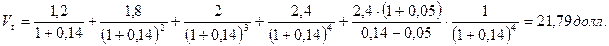
Таким образом, в условиях эффективного рынка акции данной компании на момент оценки должны продаваться по цене, примерно равной 21,79 долл.
б) Согласно формуле Гордона текущая цена обыкновенной акции очень чувствительна к параметру 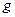 : даже незначительное его изменение может существенно повлиять на цену. Поэтому в расчетах иногда пытаются разбить интервал прогнозирования на подынтервалы, каждый из которых характеризуется собственным темпом прироста. Так, если выделить два подынтервала с темпами прироста
: даже незначительное его изменение может существенно повлиять на цену. Поэтому в расчетах иногда пытаются разбить интервал прогнозирования на подынтервалы, каждый из которых характеризуется собственным темпом прироста. Так, если выделить два подынтервала с темпами прироста 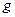 и
и 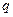 соответственно, то формула
соответственно, то формула 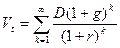 принимает вид:
принимает вид:
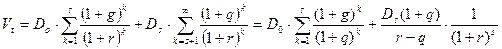
где 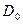 — дивиденд, выплаченный в базисный момент времени;
— дивиденд, выплаченный в базисный момент времени;
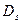 — прогноз дивиденда в
— прогноз дивиденда в 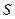 -м периоде
-м периоде
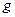 — прогноз темпа прироста дивиденда в первые
— прогноз темпа прироста дивиденда в первые 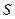 периодов;
периодов;
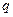 — прогноз темпа прироста дивидендов в последующиепериоды.
— прогноз темпа прироста дивидендов в последующиепериоды.
Пример.За прошедший год компания выплатила в качестве дивидендов по 10$ на акцию. Ожидается, что в течение следующих трех лет дивиденд будет расти на 3% в год, затем темп прироста снизится до 2% в год на весь оставшийся период. Определить теоретическую стоимость акции, если рыночная норма прибыли составляет 10%.
Решение: D0 =10$; g = 0,03; q =0,02; S = 3.
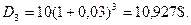
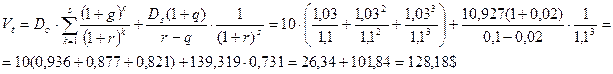
§
§
Предположим, что вексель продан через некоторое время после его покупки до наступления срока его погашения. Эффективность этой операции может быть измерена с помощью простых или сложных процентов. При этом финансовая результативность зависит от разности цен купли-продажи, которая определяется уровнем учетных ставок и сроками до погашения векселя. Дисконтирование может производиться по простой или сложной учетным ставкам.
Пусть номинал векселя равен 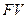 рублей. Вексель был куплен по учетной ставке
рублей. Вексель был куплен по учетной ставке 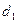 за
за 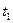 дней до наступления срока.
дней до наступления срока.
а). Дисконтирование производится по простой учетной ставке за 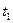 дней до срока погашения.
дней до срока погашения.
Цена векселя в момент покупки составила 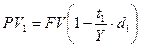
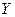 -временная база учета для вексельных операций, как правило,
-временная база учета для вексельных операций, как правило, 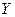 = 360 дней
= 360 дней
За 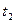 дней до погашения вексель был продан по ставке
дней до погашения вексель был продан по ставке 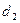 по цене
по цене
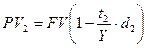
б) Для средне- и долгосрочных операций с векселями, как правило, применяется сложная учетная ставка.
Пусть цена векселя в момент покупки за 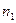 лет до погашения составила:
лет до погашения составила:
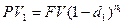
За 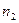 лет до погашения вексель был продан по ставке
лет до погашения вексель был продан по ставке 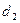 по цене
по цене
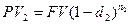
Доходность подобных операций может быть оценена с помощью простой или сложной процентных ставок. В первом случае процентная ставка может быть определена по формуле:
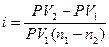
Замечание: Для краткосрочного периода 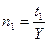 ;
; 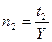 ;
;
Во втором случае доходность может быть оценена с помощью сложной процентной ставки по формуле:
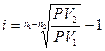
Пример. Вексель номиналом 100 тыс. рублей куплен за 150 дней до его погашения, простая учетная ставка – 15%.Через 30 дней его реализовали по простой учетной ставке 12%. Оцените эффективность финансовой операции в виде простой процентной ставки.
Решение: 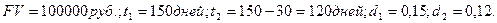
Цена векселя в момент покупки:
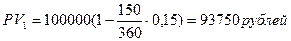
Цена продажи векселя составила:
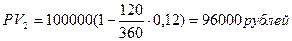
Оценим доходность финансовой операции с помощью простой процентной ставки:
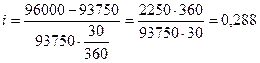 или 28,8%
или 28,8%
Пример. Вексель номиналом 200000 рублей куплен за 5 лет до срока погашения. Сложная учетная ставка – 10%. Через три года его продали по сложной учетной ставке 8%. Оценить эффективность этой финансовой операции в виде сложной учетной ставки.
Решение:
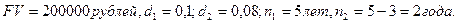
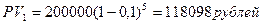
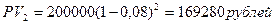
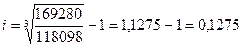 или 12,75%
или 12,75%
§
Рассмотрим, как оценивается доходность финансовой операции покупки валюты. Предположим, некоторая сумма в объеме PV рублей обменена на валюту. Затем через период n лет совершен ее обмен на рубли.
Обозначим сумму в рублях на начало операции 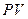 ;
;
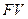 – сумма в рублях на конец операции;
– сумма в рублях на конец операции;
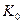 и
и 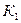 – курс обмена в начале и в конце операции соответственно, имеющий размерность, например, в руб./долл. или в руб./евро. Иначе говоря,
– курс обмена в начале и в конце операции соответственно, имеющий размерность, например, в руб./долл. или в руб./евро. Иначе говоря, 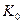 – банковский курс продажи валюты,
– банковский курс продажи валюты, 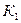 – банковский курс покупки валюты.
– банковский курс покупки валюты.
Сумма, полученная в результате проведенной операции, может быть определена по формуле:
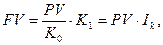 где
где 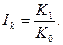
Поскольку в течение n лет в результате инфляции покупательная способность полученной суммы в определенной степени снизилась, то ее реальная покупательная способность  может быть определена по формуле:
может быть определена по формуле:
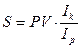 . Здесь
. Здесь 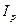 – индекс цен за период n лет.
– индекс цен за период n лет.
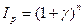 , где
, где 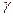 – среднегодовой темп инфляции.
– среднегодовой темп инфляции.
Определим доходность рассматриваемой финансовой операции в виде сложной годовой процентной ставки 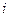 из равенства:
из равенства:
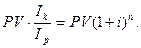
Выразив из этого равенства 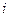 , найдем формулу для определения доходности операции покупки валюты:
, найдем формулу для определения доходности операции покупки валюты:
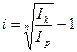 .
.
Доходность такой операции равна нулю, если выполняется условие 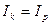 . При
. При 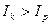 операция будет доходной, а при
операция будет доходной, а при 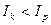 – убыточной.
– убыточной.
Пример. Предприниматель, имея свободную сумму 500 тыс. рублей предполагает приобрести на нее валюту с целью сохранения средств от инфляции, с тем, чтобы через 1,5 года вновь обменять валюту на рубли и приобрести на эти средства необходимое оборудование. На начало финансовой операции цена покупки доллара банком составляет 24, 15 руб., а цена продажи – 24,20 рублей. Для евро эти показатели соответственно 34, 65 руб. и 34, 75 руб. Предполагается, что концу срока цена покупки долларов банком составит 24,75 руб., а цена продажи – 24,85 руб. Аналогичные показатели для евро на конец операции – 36, 50 руб. и 36, 60 руб. Среднегодовой темп инфляции прогнозируется на уровне 7,5%.
Определить:
а) сумму в рублях, полученную в результате операции покупки-продажи долларов и евро;
б) покупательную способность полученных сумм с учетом инфляции:
в) доходность финансовых операций;
г) курс покупки валюты банком в конце операции, который обеспечил бы полное сохранение средств от инфляции.
Решение:
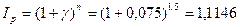 .
.
Таким образом, за 1,5 года цены возрастут на 11,46% ,
а) 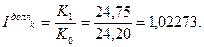
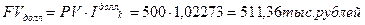
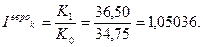
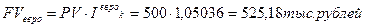
Из произведенных расчетов видно, что операция с евро в данном случае дает лучший результат.
б) Скорректируем этот результат с поправкой на инфляцию:
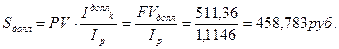
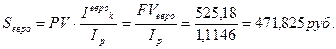
Следовательно, не удается полностью сохранить деньги от инфляции.
в) Определим доходность рассматриваемых финансовых операций.
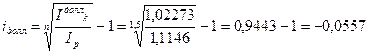 .
.
Операция с долларами является убыточной. Ее доходность отрицательна и составляет – 5,57%.
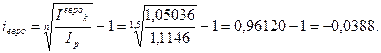
Операция с евро также убыточна. Ее доходность составляет – 3,88%.
г) Определим, при каком курсе покупки валюты в конце срока, операции по покупке-продаже валюты были бы безубыточны. Для этого используем равенство: 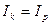 .
.
Оно выполняется в случае покупки долларов, если 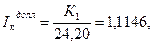 то есть при
то есть при 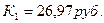 Таким образом, при курсе покупки долларов банком по цене 26,97 руб. удается сохранить деньги от инфляции. Для получения прибыли от такой операции, курс покупки должен превысить этот уровень.
Таким образом, при курсе покупки долларов банком по цене 26,97 руб. удается сохранить деньги от инфляции. Для получения прибыли от такой операции, курс покупки должен превысить этот уровень.
Аналогично определим критическое значение курса евро из равенства: 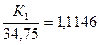 . Отсюда
. Отсюда 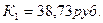
Полученный пример показывает, что достаточно сложно уберечь деньги от инфляции, не инвестируя их с целью наращения процентов.
§
Рассмотрим финансовые операции, совмещающие конверсию валюты с наращением процентов. Для того чтобы найти возможности наилучшего размещения денежных средств (с конверсией или без нее), необходимо сравнить результаты непосредственного размещения денежных средств и опосредованно через другую валюту.
Существует четыре варианта для наращения процентов:
1) СКВ 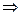 СКВ;
СКВ;
2) СКВ→Руб 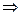 Руб→СКВ;
Руб→СКВ;
3) Руб 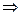 Руб
Руб
4) Руб→СКВ 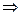 )СКВ→Руб
)СКВ→Руб
Здесь → означает процесс конверсии; 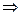 означает процесс наращения.
означает процесс наращения.
Вариант 1 и 3 не представляют интереса, т.к. здесь применяются обычные формулы наращения простых и сложных процентов.
В операциях наращения с конверсией валют можно выделить три этапа: обмен валюты, наращение процентов на полученную сумму и конвертирование в исходную валюту. При этом существует два источника дохода: изменение курса валют и наращение процента. Причем если второй из них является безусловным источником дохода (ставка процента фиксирована), то этого нельзя сказать о первом. Более того, двойное конвертирование валюты может быть как прибыльным, так и убыточным.
Вариант СКВ→Руб 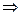 Руб→СКВ.
Руб→СКВ.
Введем следующие обозначения: *
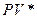 — исходная сумма в валюте;
— исходная сумма в валюте;
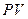 — исходная сумма депозита в рублях;
— исходная сумма депозита в рублях;
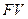 — наращенная сумма депозита в рублях;
— наращенная сумма депозита в рублях;
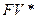 — наращенная сумма в валюте;
— наращенная сумма в валюте;
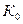 — курс покупки валюты в начале операции;
— курс покупки валюты в начале операции;
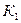 — курс продажи валюты в конце операции;
— курс продажи валюты в конце операции;
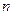 — срок депозита;
— срок депозита;
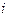 — ставка наращения простых процентов на рублевых депозитах;
— ставка наращения простых процентов на рублевых депозитах;
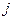 — ставка наращения для валютного депозита в валюте конкретного вида.
— ставка наращения для валютного депозита в валюте конкретного вида.
(Знак * показывает, что величина измеряется в денежных единицах выбранной валюты).
Эта финансовая операция предполагает обмен валюты в количестве 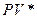 на рубли, наращение на полученную в рублях сумму
на рубли, наращение на полученную в рублях сумму 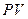 простых процентов по ставке
простых процентов по ставке 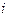 и конвертирование в исходную валюту. Рассматривая этот процесс поэтапно, получим следующие результаты:
и конвертирование в исходную валюту. Рассматривая этот процесс поэтапно, получим следующие результаты:
1) 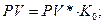
2) 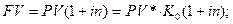
3) 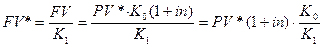 .
.
Таким образом, процесс наращения с конверсией валюты в этом случае выражается формулой:
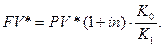
Нетрудно видеть, что результат операции в случае наращения по сложным процентам может быть определен по формуле:
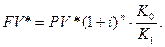
Доходность операции будет нулевой, если 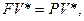 т.е. при
т.е. при 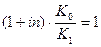 если наращение произведено по простым процентам и
если наращение произведено по простым процентам и 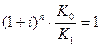 при наращении по сложным процентам.
при наращении по сложным процентам.
Следовательно, критическое значение курса продажи валюты в конце финансовой операции 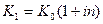 в случае, если проценты простые, и
в случае, если проценты простые, и 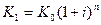 для сложных процентов.
для сложных процентов.
В случае если 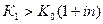 , то операция будет убыточной в случае наращения по простым процентам.
, то операция будет убыточной в случае наращения по простым процентам.
Для наращения по сложным процентам операция становится убыточной в случае, если выполняется неравенство: 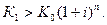
Пример.Предприниматель намерен поместить 5000 $ на рублевый депозит на 4 месяца. Курс покупки долларов на начало финансовой операции составляет 25,3руб. за доллар. Ожидаемый курс продажи – 25,85руб. за доллар. Процентная ставка по рублевым депозитам 9%. Проценты простые. Определите:
а) наращенную сумму в долларах;
б) доходность операции с конверсией;
в) критическое значение курса продажи доллара в конце сделки, при котором проведение финансовой операции целесообразно.
Решение:
а) Наращенная сумма:
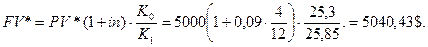
б) Доходность операции с конверсией 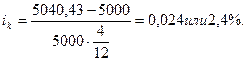
в) Критическое значение 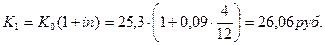
В случае если 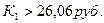 , операция становится убыточной.
, операция становится убыточной.
Поскольку в момент заключения контракта значение курса продажи валюты в конце сделки 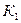 неизвестно, полезно знать его максимально допустимое значение, при котором эффективность операции наращения с конверсией валюты будет равна существующей ставке по соответствующим валютным депозитам. В этом случае применение двойного конвертирования не дает дополнительной выгоды.
неизвестно, полезно знать его максимально допустимое значение, при котором эффективность операции наращения с конверсией валюты будет равна существующей ставке по соответствующим валютным депозитам. В этом случае применение двойного конвертирования не дает дополнительной выгоды.
Предположим, процентная ставка по валютным депозитам равна 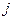 .
.
Тогда максимально допустимое значение 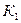 может быть определено из равенства:
может быть определено из равенства:

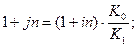
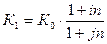 .
.
Таким образом, если 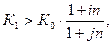 то проводить конверсию валюты нецелесообразно.
то проводить конверсию валюты нецелесообразно.
Пример. В условиях предыдущей задачи определить максимальное значение курса продажи долларов в конце операции, если процентная ставка по долларовому депозиту равна 4%.
Решение:
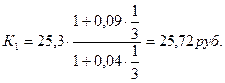
Поскольку в конце операции ожидают, что значение курса продажи долларов будет 25,85руб. за доллар (больше, чем 25,72 руб. за доллар), то применять конверсию нецелесообразно, а лучше положить валюту на долларовый депозит.
Для того, чтобы убедиться в этом, определим наращенную сумму на долларовом депозите:
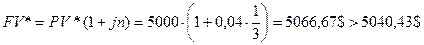
Следовательно, в этом случае производить конверсию нецелесообразно.
Вариант Руб →СКВ 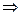 СКВ → Руб
СКВ → Руб
Данная финансовая операция предполагает обмен денежной суммы в рублях в количестве 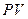 валюту, наращение на полученную сумму
валюту, наращение на полученную сумму 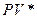 процентов по ставке
процентов по ставке 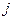 и конвертирование валюту наращенной суммы в валюте в рубли. Рассматривая этот процесс поэтапно, получим следующие результаты:
и конвертирование валюту наращенной суммы в валюте в рубли. Рассматривая этот процесс поэтапно, получим следующие результаты:
1) 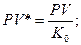
2) 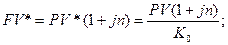
3) 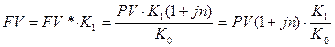 .
.
Таким образом, процесс наращения с конверсией в этом случае выражается формулой:
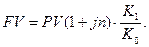
Результат операции в случае наращения по сложным процентам может быть определен по формуле:
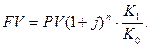
Доходность операции будет нулевой, если 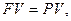 т.е. при
т.е. при 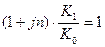 если наращение произведено по простым процентам и
если наращение произведено по простым процентам и 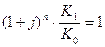 при наращении по сложным процентам.
при наращении по сложным процентам.
Критическое значение курса продажи валюты в конце финансовой операции 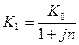 в случае, если проценты простые, и
в случае, если проценты простые, и 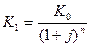 для сложных процентов.
для сложных процентов.
В случае если 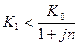 , то операция будет убыточной в случае наращения по простым процентам.
, то операция будет убыточной в случае наращения по простым процентам.
Для наращения по сложным процентам операция становится убыточной в случае, если выполняется неравенство: 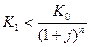
Определим значение 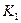 , при котором эффективность операции наращения с конверсией будет равна существующей ставке по рублевому депозиту. В этом случае применение двойного конвертирования не дает дополнительной выгоды.
, при котором эффективность операции наращения с конверсией будет равна существующей ставке по рублевому депозиту. В этом случае применение двойного конвертирования не дает дополнительной выгоды.
Тогда минимально допустимая величина 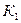 может быть определено из равенства:
может быть определено из равенства:

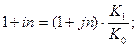
Отсюда 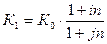 .
.
Если 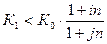 , то нецелесообразно проводить конверсию, а лучше положить деньги на рублевый депозит.
, то нецелесообразно проводить конверсию, а лучше положить деньги на рублевый депозит.
Пример.Предприниматель, имея сумму в размере 400 тыс. рублей, предполагает поместить ее на долларовом депозите на 3 месяца под процентную ставку 5% годовых, а затем обменять полученную сумму на рубли. Курс продажи долларов на начало срока депозита 25,45 руб., ожидаемый курс покупки через 3 месяца 25,85 руб. Процентная ставка на рублевом депозите 10%. Выяснить целесообразность этой сделки.
Решение:
Оценим целесообразность проведения конверсии. Для этого сравним значения 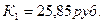 и
и 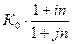 .
.
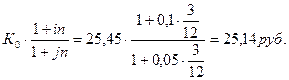
Следовательно, целесообразно провести операцию с конверсией. Чтобы убедиться в этом, сравним результаты наращения с конверсией и без нее.
1) наращенная сумма с конверсией:
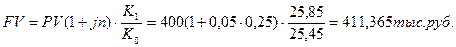
2) наращенная сумма на рублевом депозите (без конверсии):
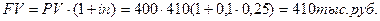
§
Основные понятия и базовые принципы страхования
Страховщик – специализированная организация, проводящая страхование,
Страхователь – физическое или юридическое лицо, уплачивающее страховые взносы и вступающее в конкретные страховые отношения со страховщиком.
Объекты и предметы страхования – подлежащие страхованию материальные ценности, в личном страховании – жизнь, здоровье и трудоспособность страхователя или застрахованного лица.
Страховая сумма – сумма денежных средств, на которую фактически застрахованы имущество, жизнь, здоровье.
Страховой тариф – процентная ставка от совокупной страховой суммы. Страховой тариф служит основой для формирования страхового фонда.
Финансовые расчеты в страховании (актуарные расчеты) базируются на двух основных принципах – финансовой эквивалентности обязательств страхователя и страховщика, учета фактор времени и солидарности застрахованных.
Согласно принципу финансовой эквивалентности обязательств теоретическая себестоимость страховой операции – нетто-премия должна быть равна стоимости страхования. Этот принцип реализуется с помощью уравнения, в котором нетто-премия приравнивается к актуарной стоимости страховых платежей, которая представляет собой современную стоимость страховых выплат с учетом условий страхования.
Учет фактора времени достигается с помощью дисконтирования платежей – приведения их к начальному моменту времени.
Например, пусть страхователь в возрасте 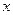 лет заключил договор со страховщиком, согласно которому последний выплатит ему сумму
лет заключил договор со страховщиком, согласно которому последний выплатит ему сумму  при достижении возраста
при достижении возраста 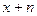 лет. Предположим, вероятность дожития до этого возраста равна
лет. Предположим, вероятность дожития до этого возраста равна 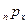 . Тогда математическое ожидание выплаты составит
. Тогда математическое ожидание выплаты составит 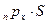 . Поскольку выплаты премии и страховых сумм производятся в разное время, найдем современную стоимость платежа А с учетом вероятности его выплаты с помощью операции дисконтирования:
. Поскольку выплаты премии и страховых сумм производятся в разное время, найдем современную стоимость платежа А с учетом вероятности его выплаты с помощью операции дисконтирования:
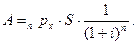 (11.1) Здесь
(11.1) Здесь 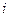 – сложная годовая процентная ставка.
– сложная годовая процентная ставка.
Величина А представляет собой математическое ожидание дисконтированной страховой выплаты, то есть актуарную стоимость страховой выплаты. Нетто-премия при страховании на дожитие равна этой величине.
Принцип солидарности застрахованных подразумевает согласованность интересов. Например, в негосударственном пенсионном страховании пенсии выплачиваются из накоплений всех участников данного вида страхования, доживших и не доживших до их получения. То есть пенсионные расходы распределяются между всеми участниками. В результате цена страхования пенсии оказывается меньше, чем обеспечение такой же пенсии по сберегательной схеме, то есть без учета фактора солидарности.
Аналогично при страховании на дожитие страховая выплата обеспечивается не только собственным взносом застрахованного лица, но и взносами тех, кто не дожил до этого возраста.
В медицинском страховании в соответствие с принципом солидарности участники, у которых затраты на лечение незначительны или вовсе отсутствуют, оплачивают часть медицинских расходов участников с более высокими расходами на эти цели поскольку расходы распределяются между всеми застрахованными.
§
Для определения размера денежных выплат каждого страхователя, как участника солидарной ответственности, рассчитывается тарифная нетто-ставка, используемая для расчета страхового платежа – основного источника дохода страховщика. Расчет нетто-ставки базируется на оценке вероятности наступления страховых случаев.
Нетто-ставка – основная часть страхового тарифа. Она формирует страховой фонд и устанавливается условиями страхования. Для рисковых видов страхования в состав нетто-ставки включается рисковая надбавка, которая учитывает отклонения возможных выплат от их среднего уровня и формирует запасной фонд.
Страховой и запасной фонд предназначены для расчетов со страхователями: выплаты суммы страховых возмещений, отчислений в резервный фонд, отчислений на предупредительные мероприятия.
Брутто-ставка включает в себя нетто-ставку и нагрузку. Нагрузка обеспечивает расходы на ведение дела и прибыль страховой кампании. За счет нагрузки страховщик оплачивает труд работников, содержание помещений и пр. Нагрузка, как правило, составляет 10-20% брутто-ставки. Брутто-ставка может быть рассчитана на основе соотношения:
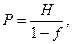 (11.2)
(11.2)
где Р – брутто-ставка, Н – нетто-ставка, f – доля нагрузки в брутто-ставке.
Страхование жизни
Рассмотрим основные виды страхования жизни.
а). Страхование на дожитие. Выплата производится при условии дожития застрахованного лица до определенного возраста и полной оплаты соответствующего договора очередными или единовременными взносами.
б).Страхование на случай смерти. Страховая сумма выплачивается только при наступлении смерти застрахованного в период действия договора.
в) Страхование от несчастных случаев.Выплата производится, если физическое лицо пострадает от несчастного случая. Под несчастным случаем подразумевается физическое повреждение, следствием которого может быть временная инвалидность, постоянная инвалидность, смерть.
г) Смешанное страхование жизни. Этот вид страхования объединяет в одном договоре страхование на дожитие, на случай смерти и страхование от несчастных случаев. Нетто-ставка по смешанному страхованию рассчитывается как сумма нетто-ставок его составляющих.
§
Условия страхования жизни обычно предусматривают выплаты в связи с дожитием застрахованного лица до окончания действия договора страхования или в случае его смерти в течение этого срока.
Вероятность дожить до определенного возраста или окончания срока страхования зависит в первую очередь от возраста в момент страхования и срока действия договора страхования жизни.
Она определяется с помощью таблицы смертности населения. Эта таблица разработана на основе данных демографической статистики (дифференцированно для мужчин и женщин). Таблица содержит конкретные цифры смертности для каждого возраста в расчете на 100000 населения. На основе этих таблиц рассчитывают страховые тарифы.
Возраст человека обозначается символом 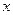 , а число лиц, доживающих до возраста
, а число лиц, доживающих до возраста 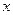 , обозначается
, обозначается 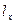 . Число умирающих при переходе от возраста
. Число умирающих при переходе от возраста 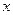 к возрасту
к возрасту 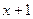 обозначается символом
обозначается символом 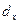 .
.
Вероятность умереть в возрасте 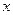 лет, не дожив до возраста
лет, не дожив до возраста 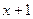 лет:
лет:
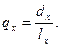 (11.3)
(11.3)
Например, из 100 000 родившихся женщин до 50 лет доживают 90792 чел. ( 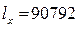 ), до 51 года не доживают 459 чел. (
), до 51 года не доживают 459 чел. ( 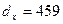 ), следовательно, вероятность умереть в возрасте 50 лет у женщин:
), следовательно, вероятность умереть в возрасте 50 лет у женщин:
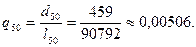
Используя таблицу смертности, страховщик может определить величину страхового фонда, необходимого для выплаты в обусловленные сроки страховых сумм.
Используя метод дисконтирования можно определить его современную стоимость, равную сумме, которую необходимо собрать со страхователей в момент заключения договора страхования.
Страховые взносы могут вноситься единовременно при заключении договора страхования или ежегодно, образуя финансовую ренту. Рассмотрим некоторые случаи определения нетто-ставок.
§
Условия страхования предусматривают выплаты в связи с дожитием застрахованного лица до окончания срока договора. С помощью таблицы смертности устанавливается вероятное число выплат по дожитию застрахованного лица до окончания срока страхования. На основе данных о страховых суммах определяется размер страхового фонда, необходимого для страховых выплат.
Предположим, страхователь в возрасте 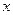 лет заключил договор со страховщиком, согласно которому последний выплатит ему сумму
лет заключил договор со страховщиком, согласно которому последний выплатит ему сумму  при достижении возраста
при достижении возраста 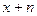 лет. Обозначим вероятность дожития до этого возраста
лет. Обозначим вероятность дожития до этого возраста 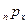 .
.
Тогда 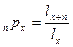 , где
, где 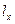 – число лиц, заключивших договор страхования в возрасте
– число лиц, заключивших договор страхования в возрасте 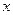 лет,
лет, 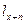 – число лиц, доживших до окончания договора страхования.
– число лиц, доживших до окончания договора страхования.
Математическое ожидание выплаты составит
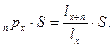 (11.4)
(11.4)
Дисконтируя эту величину по сложной процентной ставке 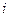 , определим математическое ожидание дисконтированной страховой выплаты, то есть актуарную стоимость страховой выплаты или величину единовременного взноса (без учета нагрузки):
, определим математическое ожидание дисконтированной страховой выплаты, то есть актуарную стоимость страховой выплаты или величину единовременного взноса (без учета нагрузки):
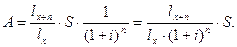 (11.5)
(11.5)
Предположим, 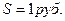 Тогда единовременная нетто-ставка по страхованию на дожитие определяется по формуле:
Тогда единовременная нетто-ставка по страхованию на дожитие определяется по формуле:
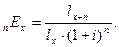 (11.6)
(11.6)
Пример.Страховщик заключил договор страхования с мужчиной 45 летнего возраста на 5 лет на дожитие на сумму 20 000 руб. Необходимо определить единовременную страховую премию при условии, что нагрузка составляет 10%. Страховщик предполагает всю сумму страховых взносов инвестировать под 9% годовых.
Решение:
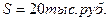 Согласно таблице смертности
Согласно таблице смертности 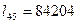 ;
; 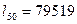 .
.
Определим нетто-ставку:
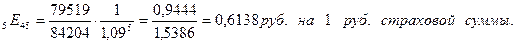
Найдем брутто-ставку, учитывая, что нагрузка 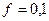 по формуле (11.2):
по формуле (11.2):
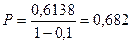
Следовательно, величина единовременного взноса составит: 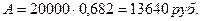
При единовременном взносе страхователь сразу при заключении договора погашает свои обязательства перед страховщиком и в дальнейшем не производит никаких дополнительных взносов.
§
Этот вид страхования является наиболее распространенным. Страховая сумма, равная  выплачивается в случае смерти застрахованного. Допустим договор заключен в возрасте
выплачивается в случае смерти застрахованного. Допустим договор заключен в возрасте 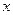 лет. Если застрахованный умрет на первом году страхования, а выплата страховых сумм наследникам производится в конце года наступления страхового события, то с учетом его вероятности современная величина выплаты (на момент заключения договора) составит:
лет. Если застрахованный умрет на первом году страхования, а выплата страховых сумм наследникам производится в конце года наступления страхового события, то с учетом его вероятности современная величина выплаты (на момент заключения договора) составит:
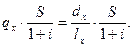
Если страховой случай наступит во втором году, то современная величина выплаты равна: 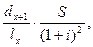 и т.д.
и т.д.
Единовременную нетто-ставку в расчете на 1 руб. страховой суммы ( 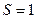 ) определим на основе принципа эквивалентности обязательств, в соответствии с которым искомая сумма должна быть равна математическому ожиданию суммы страховых выплат:
) определим на основе принципа эквивалентности обязательств, в соответствии с которым искомая сумма должна быть равна математическому ожиданию суммы страховых выплат:
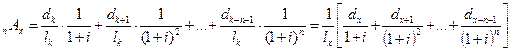 (11.7),
(11.7),
где 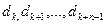 – количество умирающих в течение срока страхования.
– количество умирающих в течение срока страхования.
При смешанном страховании на дожитие и на случай смерти совокупная нетто-ставка определяется по формуле:
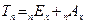 (11.8)
(11.8)
Пример. Определить единовременную нетто-ставку и страховую премию для мужчины 55 летнего возраста, оформляющего страховку на случай своей смерти сроком на 5 лет на сумму 10 тыс. руб. Страховая компания предполагает поместить страховую сумму под 9% годовых. Нагрузка составляет 12%.
Решение:
Выберем из таблицы смертности число умерших в интервале от 55 до 59 лет;
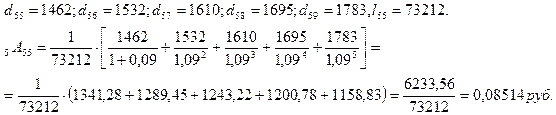
Учитывая, что нетто-ставка составляет 0,08514 рублей, а нагрузка 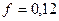 , определим брутто-ставку:
, определим брутто-ставку:
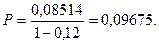
Величина единовременного взноса составит:
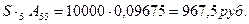
§
При расчете единовременной нетто-ставки предполагается, что сумма подлежащих оплате взносов погашаются единовременно в момент заключения договора о страховании. Однако чаще всего страхователи предпочитают платить взносы в течение всего срока страхования. В связи с этим возникает необходимость расчета годичных нетто-ставок.
Единовременная нетто-ставка отличается по величине от годичной ставки по ряду причин. Во-первых, при единовременной уплате страхового взноса он может быть сразу после его поступления инвестирован под проценты. Годичные же взносы поступают постепенно, в связи с чем сумма начисленных процентов будет значительно меньше, чем при единовременном взносе. В результате страховщик получит меньший страховой фонд. Во-вторых, страховой фонд выплачивают все лица, заключившее страховой договор, а при годичной уплате ряд страхователей прекратит взносы в результате своей смерти.
Следовательно, при расчете годичной нетто-ставки необходимо учитывать частичную потерю сумм и снижение числа платежей в результате смерти некоторой части застрахованных.
Предположим, что все мужчины, достигшие возраста 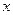 лет, обязались в конце каждого страхового года вносить страховой компании 1 руб. в течение
лет, обязались в конце каждого страхового года вносить страховой компании 1 руб. в течение 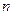 лет. Тогда в конце первого года будет внесено
лет. Тогда в конце первого года будет внесено 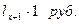
Современная стоимость этой суммы составит 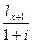 , где
, где 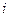 – норма накопления данной страховой компании. Во втором году современная стоимость взносов составит
– норма накопления данной страховой компании. Во втором году современная стоимость взносов составит 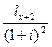 , в третьем –
, в третьем – 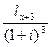 , в
, в 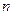 году –
году – 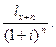
Таким образом, современная стоимость финансовых обязательств страховщика, относящихся ко всем 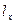 лицам выразится суммой:
лицам выразится суммой:
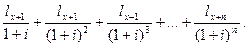
Для получения современной стоимости финансовых обязательств по отношению к одному лицу, то есть годичной нетто-ставки, эту сумму необходимо поделить на 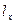 – число лиц, заключивших договор:
– число лиц, заключивших договор:
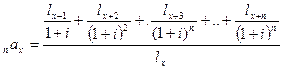 (11.9)
(11.9)
Значение 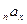 можно рассматривать как коэффициент рассрочки. Зная его значение, можно определить годичный взнос по формуле:
можно рассматривать как коэффициент рассрочки. Зная его значение, можно определить годичный взнос по формуле:
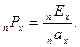 ,
,
Здесь 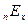 – единовременная нетто-ставка.
– единовременная нетто-ставка.
Пример. Мужчина в возрасте 45 лет, заключил договор по смешанному страхованию жизни сроком на 3 года. Страховая сумма составляет 25 тыс. руб. Норма доходности страховой компании – 8%. Доля нагрузки в брутто-ставке 10%. Определите единовременную брутто-ставку и брутто-премию; коэффициент рассрочки и величину годичного взноса.
Решение: 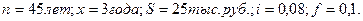
1) Определим нетто-ставку на дожитие по формуле:
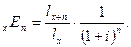
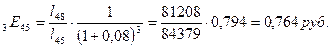
Таким образом, нетто-ставка на дожитие составляет 76,4 руб. со 100 рублей страховой суммы.
2). Определим нетто-ставку на случай смерти по формуле:
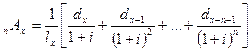
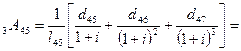
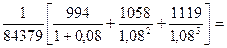
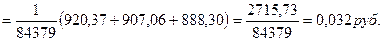
Следовательно, нетто-ставка на случай смерти составляет 3 руб.20 коп. со 100 руб. страховой суммы.
3). Нетто-ставка при смешанном страховании жизни:
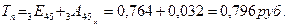
4) Определим единовременную брутто-ставку:
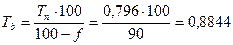
5) Брутто-премия составит 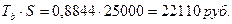
6). Определим коэффициент рассрочки:
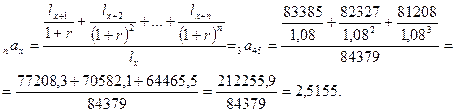
7). Учитывая, что единовременный взнос или брутто-премия составляет 22110 руб., определим годичный взнос:
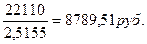
Таким образом, при выплате в рассрочку за 3 года страхователем будет уплачено 26368,52 руб.
Литература
1. Бочаров П.П., Касимов Ю. Ф. Финансовая математика.: Учебник. – М.: Гардарики, 2002
2. Капитоненко В.В. Финансовая математика и ее приложения: Учебно-практическое пособие для ВУЗов. – М.: ПРИОР,1998
3. Касимова О.Ю. Введение в финансовую математику (анализ кредитных и инвестиционных операций). – М.: Анкил, 2001
4. Ковалев В.В. Методы оценки инвестиционных проектов.- М.: Финансы и статистика, 2003.
5. Ковалев В.В., Уланов В.А. Курс финансовых вычислений. – 2-е изд. – М.: Финансы и статистика, 2002.
6. Криничанский К.В. Математика финансового менеджмента: учебное пособие. – М.: Издательство «Дело и Сервис», 2006.
7. Кузнецов Б. Т. Финансовая математика: Учебное пособие для вузов – М.: Издательство «Экзамен», 2005.
8.Лукасевич И.Я. Анализ финансовых операций. Методы, модели, техника вычислений.: Учебное пособие для вузов. – М.: Финансы, ЮНИТИ, 1998.
9. Малыхин В.И. Финансовая математика/ Учебное пособие для вузов. –М.: ЮНИТИ-ДАНА, 1999
10. Мелкумов Я.С. Финансовые вычисления. Теория и практика: Учебно-справочное пособие. – М.:ИНФРА, 2002
11. Салин В.Н., Ситникова О.Ю. Техника финансово-экономических расчетов: Учебное пособие. -М.: Финансы и статистика, 1998
12.Симчера В.М. Введение в финансовые и актуарные вычисления. – М.: Финансы и статистика, 2003
13. Уланов В.А. Сборник задач по курсу финансовых вычислений/Под ред. Проф. В.В. Ковалева. -М.: Финансы и статистика, 2000
14.Четыркин Е.М. Методы финансовых и коммерческих расчетов. – М.: «Дело-Ltd», 1995. гл. 12 «Изменение эффективности инвестиций».
Задания для самостоятельного решения
1. Фирма X собирается купить завод по производству глиняной посуды. Стоимость этого предприятия составляет 100 млн руб. Кроме того, расчеты показывают, что для модернизации этого предприятия потребуются в первый же год дополнительные затраты в сумме 50 млн руб. Однако при этом предполагается, что в последующие 8 лет этот завод будет обеспечивать ежегодные денежные поступления в сумме 25 млн руб. Предполагается, что через 10 лег фирма продаст завод по остаточной стоимости, которая составит, согласно расчетам, 80 млн руб.
Определите, будут ли инвестиции для фирмы полезными, приведут ли они к росту капитала фирмы.
2. Инвестиционный проект на сумму 2 млн руб. способен обеспечить ежегодные денежные поступления в сумме 1 млн руб.
Какой будет срок окупаемости этого проекта при желательном уровне окупаемости (коэффициенте дисконтирования) 10%?
3. Организации необходимо возвести новую котельную для отопления построенного им для своих работников жилого микрорайона. Возможно использование для этой цели грех видов топлива: угля, газа и мазута.
Проведенный заводскими энергетиками и экономистами расчет позволил построить аналитическую таблицу для каждого из вариантов энергообеспечения (для простоты анализа предполагается срок жизни всех вариантов инвестиций, равный четырем годам).
Тип топлива | 0-й год | 1 -й год | 2-й год | 3-й год | 4-й год |
Уголь | -1 000 | 750 | 500 | 0 | 0 |
Газ | -1 000 | 350 | 350 | 350 | 350 |
Мазут | -500 | 180 | 180 | 180 | 180 |
Рассчитайте: чистый доход, чистый дисконтированный доход, индекс доходности затрат и инвестиций, срок окупаемости для каждого варианта.
- 4. Используйте предыдущий пример с котельной, сравните угольную и газовую схемы не за счет искусственного приема с двукратным инвестированием в реализацию угольной технологии, а на основе эквивалентных аннуитетов для обеих схем. Для этого коэффициент дисконтирования принимается равным 10%. С его помощью проведите расчеты для периодов реализации каждого из вариантов (2 года — для угольной схемы и 4 года — для газовой).
- 5. Областная администрация должна решить вопрос о том, какую систему обогрева — водяную или электрическую — следует включить в проект реконструкции здания больницы.
Коэффициент дисконтирования при анализе принимается на уровне 10%. Срок службы водяной системы отопления равен пяти годам, а дисконтированные текущие затраты но се созданию и поддержанию составят за этот срок 100 млн руб. Для системы электрообогрс- ва аналогичные показатели составят 7 лет и 120 млн руб.
Какому варианту следует отдать предпочтение?
6. АО планирует осуществление инвестиционного проекта, предполагающего ежегодные вложения но 100 млн руб. в течение 3 лет, после чего — в начале четвертого года — новый объект можно начать использовать. По расчетам, это обеспечит АО получение чистого дохода (после уплаты налогов) в размере 100 млн руб. ежегодно на протяжении 5 лет.
Ставка дисконтирования в АО принята на уровне 10% в год. Оцените приемлемость инвестиционного проекта применительно к дате сдачи нового объекта в эксплуатацию.
7. 000 приняло решение приобрести новые швейные машины. Поскольку шансов на привлечение капитала за счет его преобразования в ОАО и эмиссии акций крайне малы, то получить средства можно только за счет кредитов.
По расчетам, для такой закупки потребуется 12 млн руб., срок жизни проекта составляет 1 год, он обеспечит приток денежных средств в сумме 1,5 млн руб. Средняя ставка для мелких заемщиков составляет в данный период 10%.
Определите, какую сумму согласятся в этих условиях инвесторы предоставить ООО в обмен на возможность получить через год денежные поступления в размере 13,5 млн руб. (12 1,5).
8. Допустим, что фирма нс ООО, а ЗАО и оно должно решить ту же задачу — приобрести новые швейные машины. По расчетам, для такой закупки потребуется 12 млн руб. Срок жизни проекта составляет 1 год, он обеспечит приток денежных средств в сумме 1,5 млн руб. Проработка проекта показала, что на ‘/, он может быть профинансирован за счет дополнительной эмиссии акций для существующих акционеров, а на У4 его придется финансировать за счет заемного капитала.
Средняя ставка для мелких заемщиков составляет в данный период 8%. Акционеры же требуют доходы на уровне 12%. У них есть на это причины; их права подлежат удовлетворению после погашения обязательств перед кредиторами, а значит, их вложения подвергаются большему риску.
В итоге ЗАО получило 9 млн руб. в виде кредита и 3 млн руб. поступления от эмиссии. Какова должна быть прибыльность данного инвестиционного проекта, чтобы удовлетворить всех инвесторов?
9. ЗАО получило инвестиции в сумме 12 млн руб., о которых говорилось в предыдущем примере, а теперь ему нужны новые средства для установки более современных гладильных прессов. При этом руководство фирмы хотело бы сохранить прежнюю структуру финансирования: 75% за счет кредита и 25% за счет эмиссии акций.
Но ситуация на денежном рынке изменилась — теперь кредиторы требуют платы за заемные средства на уровне уже 10%, тогда как акционеры согласны приобрести дополнительные акции лишь под обещание дивидендов на уровне 14%, полагая, что именно такой уровень дохода они могли бы получить по вложениям в другие сферы с тем же уровнем риска.
Определите маржинальную стоимость дополнительных инвестиций.
10. Акционерное общество обладает 1 млрд руб. инвестиционных ресурсов, стоимость которых (минимально приемлемая доходность) равна 10% годовых. При этом привлечение дополнительных средств с денежного рынка возможно лишь под 15%.
В этой ситуации вполне обоснованным представляется решение директората АО об установлении при выборе инвестиций ставки реинвестирования на уровне 12%, поскольку при такой цене денежных средств, которая на три пункта ниже рыночной, очевидно, можно без проблем разместить большие суммы средств и поэтому она вполне приемлема как критериальный показатель.
Характеристика того набора инвестиционных возможностей (проектов), которыми обладает АО, приведена в таблице.
Данные для расчета
Проект | Сумма, млн руб. | Срок жизни, лет |
А | 500 | 5 |
В | 400 | 5 |
С | 100 | 3 |
D | 100 | 10 |
Е | 100 | 20 |
Р | 1 000 | 10 |
О | 2 000 | 20 |
Определите, какие проекты будут предпочтительными при названных ограничениях.
11. Городской мясокомбинат планирует приобрести еще один холодильник, для чего сначала необходимо подготовить соответствующее помещение. Такая подготовка займет несколько месяцев и будет рассматриваться как предынвестиционныезатраты в нулевом году. Сама же холодильная камера будет приобретена в конце первого года и будет затем эксплуатироваться в течение трех лег.
Как оценить этот инвестиционный проект, если подготовительные затраты составят 5 млн руб., стоимость самой камеры — 30 млн руб., денежные поступления во втором, третьем и четвертом году соответственно 10 млн, 15 млн и 20 млн руб., а требуемый уровень рентабельности (коэффициент дисконтирования) — 10%?
12. С целью использования ресурсов местных артезианских подземных вод рассматриваются предложения по их переработке для медицинских целей.
Компания X предлагает на российском рынке микрозаводы но производству физиологических растворов высокого качества, которые могут быть смонтированы вблизи гидрогеологических скважин. Стоимость одного завода — 12,5 млн дол., оборудование помещения для монтажа — 0,5 млн дол., продолжительность предпроизводствен- ного периода (включая монтаж силами компании, отладку режима работы оборудования, обучение персонала) — 1 год.
Среднегодовой объем продаж продукции микрозавода оценивается в 25 млн дол. (годовые текущие затраты — 19 млн дол., в том числе амортизация — 2 млн дол. в год).
В первый год требуется дополнительно инвестировать 1 млн дол. на сооружение дороги, бурение скважин, организацию снабжения, получение лицензии, выкуп помещения и г.п. С учетом нестабильной обстановки в стране ставка дисконта (ставка альтернативного безрискового вложения) принята на уровне 25%, налогообложение прибыли отсутствует. Срок работы завода в связи с высокой надежностью оборудования нс поддается оценке и принимается равным бесконечности.
Определите показатели рентабельности инвестиций, чистой текущей стоимости, внутреннюю норму доходности, срок окупаемости и проанализируйте их с точки зрения инвестиционной привлекательности проекта.
Минько л.в. инвестиции
Задание 26
Найдите IRR денежногопотока, приведенноговтаблице.
ПроектС
0
С1 С2
А –100 230 –132
Задание 27
Величинаинвестиции – 1 млн. р.; прогнознаяоценкагенерируемогопогодамдохода (тыс. р.) 344;
395; 393; 322. Рассчитайтезначенияпоказателей IRR и MIRR еслиСС = 10 %.
Задание 28
Рассчитайте IRR и MIRR проекта, еслиценакапиталаравна 10 %:
ПроектС
0
С1 С2 С3
А–1 8 –14 7
Задание 29
Поданнымочетырехпроектах, приведеннымвтаблице, полагая, чтоценакапиталасоставляет
12 %, ответьтенавопросы. Какойпроектимеетнаибольший NPV?Какойпроектимеетнаименьший
NPV? Чемуравнозначение IRR проектаП1? Чемуравнозначение IRR проектаП1, еслиденежные
потокитретьегогодасчитаютсяслишкомнепредсказуемымиипотомудолжныбытьисключеныиз
расчета?
ГодП1 П2 П3 П4
0 – 10 000 – 13 000 – 10 000 – 6000
1 6000 8000 5000 5000
2 6000 8000 5000 2000
3 2000 1000 5000 2000
Задание 30
Фирма X собираетсякупитьзаводпопроизводствуглинянойпосуды. Стоимостьэтогопредприятия
составляет 100 млн. р. Крометого, расчетыпоказывают, чтодлямодернизации, этогопредприятияпо–
требуютсявпервыйжегоддополнительныезатратывсумме 50 млн. р. Однакоприэтомпредполагает–
ся, чтовпоследующиедевятьлетэтотзаводбудетобеспечиватьежегодныеденежныепоступленияв
сумме 25 млн. р. Затем, через 10 летпредполагается, чтофирмапродастзаводпоостаточнойстоимости,
котораясоставит, согласнорасчетам, порядка 80 млн. р. Коэффициентдисконтированияравен 10 %.
Определить, будутлидляфирмыинвестицииполезными, приведутлионикростукапиталафирмы.
Задание 31
Инвестиционныйпроектпредполагаетинвестирование 600 млн. р. иполучениезатемвтечение
восьмилетденежныхпоступленийвразмере 150 млн. р. ежегодно. Определитьпериодокупаемости
(дисконтированныйинедисконтированный), еслиставкадисконтированияравна 10 %.
Задание 32
АОпланируетосуществлениеинвестиционногопроекта, предполагающегоежегодныевложенияпо
100 млн. р. втечениетрехлет, послечего – вначалечетвертогогода – новыйобъектможноначатьис–
пользовать. Порасчетам, этообеспечитАОполучениечистогодохода (послеуплатыналогов) вразмере
100 млн. р. ежегоднонапротяжениипятилет. СтавкадисконтированиявАОпринятанауровне 10 % в
год. Оценитьприемлемостьинвестиционногопроектаприменительнокдатесдачиновогообъектав
эксплуатацию.
Задание 33
§

Финансированиеинвестиционногопроекта – этообеспечениепроектаинвестиционнымиресур–
сами (денежнымисредствами, основнымииоборотнымиактивами, имущественнымиправамиинема–
териальнымиактивами, кредитами, займамиизалогами, правамиземлепользованияит.д.).
Системафинансированияинвестиционныхпроектоввключает:
•источникифинансирования;
•организационныеформыфинансирования.
Источникамифинансированияинвестициймогутбыть:
1)собственныефинансовыересурсыивнутрихозяйственныерезервыинвестора (прибыль; аморти–
зационныеотчисления; денежныенакопленияисбережениягражданиюридическихлиц; средства, вы–
плачиваемыеорганамистрахованияввидевозмещенияпотерьотаварий, стихийныхбедствийит.д.);
2)заемныефинансовыесредстваинвесторов (банковскиекредиты, облигационныезаймыидр.
средства);
3)привлеченныефинансовыесредстваинвестора (средства, получаемыеотпродажиакций, паевые
ииныевзносычленовтрудовыхколлективов, граждан, юридическихлиц);
4)денежныесредства, централизуемыеобъединениями (союзами) предприятийвустановленном
порядке;
5)инвестиционныеассигнованияизгосударственныхбюджетовРФ, республикипрочихсубъек–
товФедерациивсоставеРФ, местныхбюджетовисоответствующихвнебюджетныхфондов;
6)иностранныеинвестиции.
Корганизационнымформамфинансированияотносятся:
1)акционерноефинансирование;
2) государственноефинансирование (государственныекредитынавозвратнойибезвозвратнойос–
нове, государственныевнешниезаимствованиявинвестиционныепроекты, финансированиеврамках
федеральныхинвестиционныхпрограмм;
3) кредитование (банковскиекредитыилизинг).
Акционерноефинансированиепредставляетсобойформуполучениядополнительныхинвестицион–
ныхресурсовпутемэмиссииценныхбумаг.
Приразработкеинвестиционногопроектаоченьважновыбратьформыпривлечениякапиталаире–
шить – наращиватьлисобственныйкапитал, выпускаяценныебумагиилипривлечьзаемныйкапитал. К
способамнаращиваниякапиталаотносятся:
1)обыкновенныеакции;
2)привилегированныеакции;
3)долговыеобязательствасваррантами (илиопционами);
4)конвертируемыеоблигации;
5)субординированныеконвертируемыеоблигации;
6)облигациисфиксированнойпроцентнойставкой, неподлежащиеконвертациивакции.
Общаясуммасредств, которуюнужноуплатитьзаиспользованиеопределенногообъемафинансо–
выхресурсов, выраженнаявпроцентахкэтомуобъему, называетсяценойкапитала.
Показатель, характеризующийотносительныйуровеньобщейсуммырасходовпредприятиянапод–
держаниеоптимальногосоотношениямеждусобственнымиизаемнымисредствамихарактеризуетцену
капитала, авансированноговдеятельностькомпании, иноситназваниесредневзвешеннойценыкапи–
тала (Weighted Average Cost of Capital, WACC).
∑
=
=
n
j
jj
dk
1
WACC, (1)
гдеk
j
– ценаj-гоисточникасредств; d
j
– удельныйвесj–гоисточникасредстввобщейихсумме.
Инвестированиепредставляетсобой “предоставлениеденегвдолг” снадеждойвернутьихспри–
быльюввидеденежныхпоступлений, генерируемыхпринятымпроектом. Результативностьтакойопе–
рацииоцениваетсяспомощьюспециальногокоэффициента – ставки. Ставкарассчитываетсяпоодной
издвухформул :
•темпприроста (процентнаяставка, “нормаприбыли“, доходность)
PV
PVFV
−
=r, (2)







