Решение задач по инвестиционному анализу, с использованием excel и mathcad
Ниже приведены условия задач и текстовый отчет о решении. Закачка полного решения(файлы doc, xls и mcd в архиве zip) начнется автоматически через 10 секунд.
Задание № 1
Рассчитать основные критерии эффективности NPV, PI, IRR, MIRR,PP,PPD по заданным потокам платежей (графы 1 и 2 содержат исходные данные, графы 3 и 4 используются для проведения расчетов)
Задача 1. Процентная ставка i=12%
Решение.
Период | Поток платежей | Коэффициент дисконтирования | Дисконтированный поток платежей | ||
(t) | (CFt) |
| DCFt | Kt·t | Dt·t |
1 | 2 | 3 | 4 | 5 | 6 |
0 | -20000 | 1 | -20000 | -20000 | |
1 | 4000 | 0,892857 | 3571,4286 | 3571,43 | |
2 | 6000 | 0,797194 | 4783,1633 | 4783,16 | |
3 | 6000 | 0,71178 | 4270,6815 | 4270,68 | |
4 | 7000 | 0,635518 | 4448,6265 | 4448,63 | |
5 | 6000 | 0,567427 | 3404,5611 | 3404,56 | |
Итого | 482,46101 | -20000 | 20478,5 | ||
Сравним проекты по чистому приведенному доходу. Для проектов определяем приведенную стоимость поступлений от инвестиций по формуле:
![]() , где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
, где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
NPV = 482,46
Определим индекс прибыльности.
ИД определим по формуле:
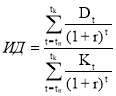
Индекс прибыльности:
ID = 20478,5/20000 = 1,024
Внутренняя норма доходности (IRR) – это такая норма дисконта, при которой сумма дисконтированных доходов за жизненный цикл проекта равна сумме дисконтированных инвестиций.
Определим внутреннюю норму доходности для каждого из проектов.
Для первого проекта решим уравнение:
∑ CFk / ( 1 IRR )k = ∑ INVt / (1 IRR) t
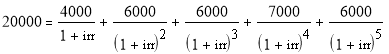
Решим уравнение аналитически, методом подбора.
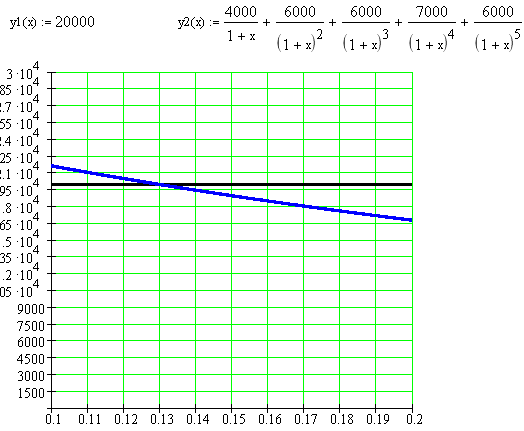
Следовательно, IRR = 0,13.
MIRR представляет собой процентную ставку, при наращении по которой в течение срока реализации проекта n общей суммы всех дисконтированных на начальный момент вложений получается величина, равная сумме всех притоков денежных средств, наращенных по той же ставке d на момент окончания реализации проекта:
( 1 MIRR )n ∑ INV / ( 1 i )t = ∑ CFk ( 1 i )n-k

MIRR = 0,179
Определим срок окупаемости для проектас учетом дисконтирования.
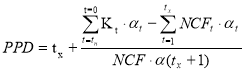
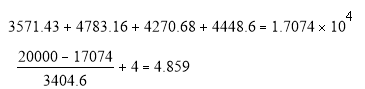
PPD = 4,4859
Определим срок окупаемости для проектабез учета дисконтирования.
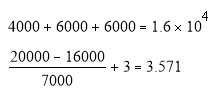
РР = 3.571
Задача 2. Процентная ставка i=12%
Решение.
Период | Поток платежей | Коэффициент дисконтирования | Дисконтированный поток платежей | ||
(t) | (CFt) |
| DCFt | Kt·t | Dt·t |
1 | 2 | 3 | 4 | 5 | 6 |
0 | -25000 | 1 | -25000 | -25000 | |
1 | 8000 | 0,892857 | 7142,8571 | 7142,86 | |
2 | 6000 | 0,797194 | 4783,1633 | 4783,16 | |
3 | 5000 | 0,71178 | 3558,9012 | 3558,9 | |
4 | 6000 | 0,635518 | 3813,1085 | 3813,11 | |
5 | 8000 | 0,567427 | 4539,4148 | 4539,41 | |
Итого | -1158,555 | -25000 | 23837,4 | ||
Сравним проекты по чистому приведенному доходу. Для проектов определяем приведенную стоимость поступлений от инвестиций по формуле:
![]() , где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
, где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
NPV = -1158,6
Определим индекс прибыльности.
ИД определим по формуле:
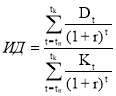
Индекс прибыльности:
ID = 23837,4/25000 = 0,953
MIRR представляет собой процентную ставку, при наращении по которой в течение срока реализации проекта n общей суммы всех дисконтированных на начальный момент вложений получается величина, равная сумме всех притоков денежных средств, наращенных по той же ставке d на момент окончания реализации проекта:
( 1 MIRR )n ∑ INV / ( 1 i )t = ∑ CFk ( 1 i )n-k
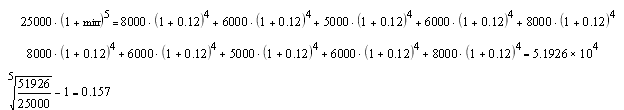
MIRR = 0,157
Определим срок окупаемости для проектабез учета дисконтирования.
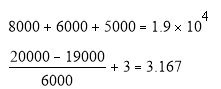
РР = 3.167
Задача 3. Процентная ставка i=13%
Решение.
Период | Поток платежей | Коэффициент дисконтирования | Дисконтированный поток платежей | ||
(t) | (CFt) |
| DCFt | Kt·t | Dt·t |
1 | 2 | 3 | 4 | 5 | 6 |
0 | -9000 | 1 | -9000 | -9000 | |
1 | 4400 | 0,884956 | 3893,8053 | 3893,81 | |
2 | 3200 | 0,783147 | 2506,0694 | 2506,07 | |
3 | 5900 | 0,69305 | 4088,996 | 4089 | |
4 | -1600 | 0,613319 | -981,30996 | -981,30 | |
Итого | 507,56069 | -9981,3 | 10488,9 | ||
Сравним проекты по чистому приведенному доходу. Для проектов определяем приведенную стоимость поступлений от инвестиций по формуле:
![]() , где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
, где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
NPV = 507,56
Определим индекс прибыльности.
ИД определим по формуле:
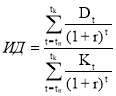
Индекс прибыльности:
ID = 10488,9/9981,3 = 1,051
Внутренняя норма доходности (IRR) – это такая норма дисконта, при которой сумма дисконтированных доходов за жизненный цикл проекта равна сумме дисконтированных инвестиций.
Определим внутреннюю норму доходности для каждого из проектов.
Для первого проекта решим уравнение:
∑ CFk / ( 1 IRR )k = ∑ INVt / (1 IRR) t
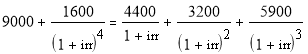
Решим уравнение аналитически, методом подбора.
Следовательно, IRR = 0,165.
MIRR представляет собой процентную ставку, при наращении по которой в течение срока реализации проекта n общей суммы всех дисконтированных на начальный момент вложений получается величина, равная сумме всех притоков денежных средств, наращенных по той же ставке d на момент окончания реализации проекта:
( 1 MIRR )n ∑ INV / ( 1 i )t = ∑ CFk ( 1 i )n-k
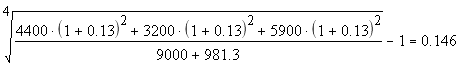
MIRR = 0,146
Определим срок окупаемости для проектас учетом дисконтирования.
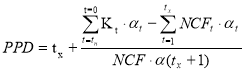
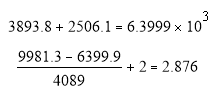
PPD = 2,876
Определим срок окупаемости для проектабез учета дисконтирования.
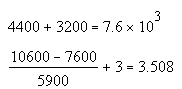
РР = 3.508
Задача 4. Процентная ставка i=8%
Решение.
Период | Поток платежей | Коэффициент дисконтирования | Дисконтированный поток платежей | ||
(t) | (CFt) |
| DCFt | Kt·t | Dt·t |
1 | 2 | 3 | 4 | 5 | 6 |
0 | -1,5 | 1 | -1,5 | -1,5 | |
1 | -1,5 | 0,925926 | -1,3888889 | -1,3888 | |
2 | -2 | 0,857339 | -1,7146776 | -1,7146 | |
3 | 0,375 | 0,793832 | 0,2976871 | 0,29769 | |
4 | 0,625 | 0,73503 | 0,4593937 | 0,45939 | |
5 | 1,25 | 0,680583 | 0,850729 | 0,85073 | |
6 | 1,25 | 0,63017 | 0,787712 | 0,78771 | |
7 | 1,25 | 0,58349 | 0,729363 | 0,72936 | |
8 | 1,25 | 0,540269 | 0,6753361 | 0,67534 | |
9 | 1,25 | 0,500249 | 0,6253112 | 0,62531 | |
10 | 1,25 | 0,463193 | 0,5789919 | 0,57899 | |
Итого | 0,4009574 | -4,6035 | 5,00452 | ||
Сравним проекты по чистому приведенному доходу. Для проектов определяем приведенную стоимость поступлений от инвестиций по формуле:
![]() , где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
, где Si – поступления в i-ый период времени, r– норма прибыли альтернативных проектов.
NPV = 0,4
Определим индекс прибыльности.
ИД определим по формуле:
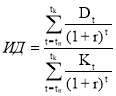
Индекс прибыльности:
ID = 5,0045/4,6035 = 1,087
Внутренняя норма доходности (IRR) – это такая норма дисконта, при которой сумма дисконтированных доходов за жизненный цикл проекта равна сумме дисконтированных инвестиций.
Определим внутреннюю норму доходности для каждого из проектов.
Для первого проекта решим уравнение:
∑ CFk / ( 1 IRR )k = ∑ INVt / (1 IRR) t
![]()
Решим уравнение аналитически, методом подбора.
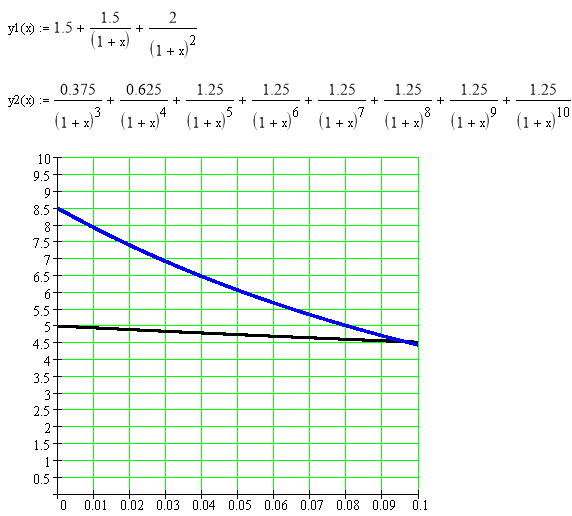
Следовательно, IRR = 0,095.
Определим срок окупаемости для проектас учетом дисконтирования.
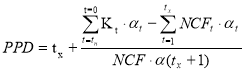
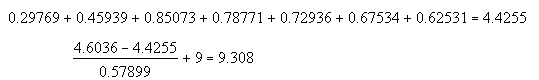
PPD = 9,308
Определим срок окупаемости для проектабез учета дисконтирования.
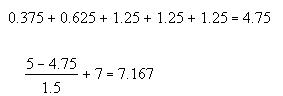
РР = 7,167.
Это ознакомительная версия работы №2245, цена оригинала 200 рублей. оформлена в программе microsoft word.
1.Продолжительность капитальных вложений в создание нового производства (новой технологической линии) составляет 4 года с равномерным распределением по годам. Потребные объемы капитальных вложений в здания, сооружения и оборудование соответственно равны: $400,000; $30000; $2,000,000.
Общий объем вложений в оборотные средства составляет $100,000.
Определить общий объем прямых капитальных вложений и его распределение по годам и структурным составляющим с учетом следующих соотношений между составляющими капитальных вложений:
- затраты на приспособления и оснастку составляют соответственно 15% и 12% от затрат на оборудование,
- затраты на транспортные средства составляют 20% от суммы затрат на сооружения и оборудование,
- затраты на приобретение технологии равны третьей части затрат на оборудование.
Решение
- Сначала вычислим общий за все 4 года обьем вложений во все приведенные компоненты капитальных вложений. Объем вложений в здания, сооружения, оборудования и оборотные средства заданы. Рассчитаем недостающие значения:
- Затраты на приспособления $2,000,000 * 0,15=$300000
- Затраты на оснастку $2000000 * 0,12=$240000
- Затраты на транспорт ($2000000 $300000)*0,20=$460000
- Затраты на технологию $2000000* 0,33=$660000
Просуммируем все компоненты вложений в основные средства. В результате получим $1444000
- Внесем все полученные и заданные данные в итоговую колонку таблицы
- Произведем распределение капитальных затрат по годам. Процедура распределения одинаковая для всех составляющих. Например, для суммарных вложений в основные средства получим:
- в 1 год $1444000*0,40=$577600
- во 2 год $1444000 * 0.20=$4288800
- в 3 год $1444000 * 0.20=$288800
- в 4 год $1444000 * 0.20=$288800
4. Распределив подобным образом все компоненты затрат, заполняем таблицу и вычисляем итоговые значения
| Прямые капитальные вложения | 1 год | 2 год | 3 год | 4 год | Всего |
| Вложения в основные средства | |||||
| Здания | 160000 | 80000 | 80000 | 80000 | 400000 |
| Сооружения | 120000 | 60000 | 60000 | 60000 | 300000 |
| Оборудование | 800000 | 400000 | 400000 | 400000 | 2000000 |
| Приспособления | 120000 | 60000 | 60000 | 60000 | 300000 |
| Оснастка | 90000 | 50000 | 50000 | 50000 | 240000 |
| Транспортные средства | 190000 | 90000 | 90000 | 90000 | 460000 |
| Технологии | 270000 | 130000 | 130000 | 130000 | 660000 |
| Вложения в оборотные средства | 40000 | 20000 | 20000 | 20000 | 100000 |
| Всего | 1790000 | 890000 | 890000 | 890000 | 4460000 |
2. Предположим, Вы заключили депозитный контракт на сумму $4,000 на 3 года при 8-и процентной ставке. Если проценты начисляются ежегодно, какую сумму Вы получите по окончании контракта?
Решение
F=P*(1 r)n
F1=4,000*(1 0,08)=$4320
F2=4,000*(1 0,08)2=$4665,6
F3=4000*(1 0.08)3=$5038,848
По окончанию депозитного контракта будет получена сумма в размере $5038,848
3. Финансовый менеджер предприятия предложил Вам инвестировать Ваши $10,000 в его предприятие, пообещав возвратить $13300 через два года. Имея другие инвестиционные возможности, Вы должны выяснить, какова процентная ставка прибыльности предложенного Вам варианта.
Решение
FVn=PV*(1 r)n
(1 r)n= FVn / PV
r=( FVn / PV )1/n – 1
r=( 13300/10000)1/2 – 1= 11,57 %
4. Предприятие собирается приобрести через пять лет новый станок стоимостью $40000. Какую сумму денег необходимо вложить сейчас, чтобы через пять лет иметь возможность совершить покупку, если процентная ставка прибыльности вложения составляет
а) 12 процентов?
б) 13 процентов?
Решение.
По условию задачи мы должны определить современное значение стоимости станка $40,000 при ставке дисконта 12 процентов. Используем формулу дисконтирования:
для случая а)
PV=FVn/ (1 r)n=40000/ (1 0, 12)5=40000*0,78=$31,200
Аналогично для случая б):
PV=FVn/ (1 r)n=40000/ (1 0, 13)5=40000*0,63=$25,200
Закономерно, что во втором случае сумма вклада получилась меньше.
5. Предприятие располагает $600,000 и предполагает вложить их в собственное производство, получая в течение трех последующих лет ежегодно $220,000. В то же время предприятие может купить на эту сумму акции соседней фирмы, приносящие 11,5 процентов годовых.
Решение.
Для ответа на вопрос можно воспользоваться двумя способами рассуждения. Сравним будущее наращенное значение аннуитета $220,000 при процентной ставке 11,5 процентов с будущим значением альтернативного вложения всей суммы $600,000 при той же процентной ставке:
- будущее значение аннуитета —
FV=CF*Znk-1(1 r)k-1 =$220,000*Z3k-1(1 11,5)=$1157,232
- будущее значение $600,000 —
FVn=PV*(1 r)n =$600000*(1 11,5)3 =$600000*1953,125=$1171,875
Результаты расчетов говорят о том, что покупка акций более выгодна, чем вложение этой же суммы денег в собственное производство.
Возможен другой подход к решению задачи, использующий приведение денежных потоков к настоящему времени. Этот подход более распространен в практике, поскольку он проще. В данном случае мы просто определяем настоящее значение аннуитета $220,000 при показателе дисконтирования 11,5 процентов:
PV=CF*Znk-1 1/(1 r)k =$220000*0,24=$589,238
Сравнивая полученное значение с суммой имеющихся в настоящее время денежных средств $600,000, приходим к такому же выводу: вкладывать деньги в акции солидной компании более выгодно.
Кто-либо может заметить, что численное значение различия альтернативных вариантов вложения в настоящее время $600,000 — $589,238 =10,762 $ существенно меньше численного различия через 3 года $1171,875-$1157,232= $14,643. Это закономерно ввиду феномена стоимости денег во времени: если мы дисконтируем $14,643 на 3 года при показателе дисконта 11,5%, то получим $10,762.
6. Предприятие рассматривает два альтернативных проекта капитальных вложений приводящих к одинаковому суммарному результату в отношении будущих денежных доходов:
| Год | Проект 1 | Проект 2 |
| 1 | $12,000 | $10,000 |
| 2 | $12,000 | $14,000 |
| 3 | $14,000 | $16,000 |
| 4 | $16,000 | $14,000 |
| 5 | $14,000 | $14,000 |
| Всего | $68,000 | $68,000 |
Оба проекта имеет одинаковый объем инвестиций. Предприятие планирует инвестировать полученные денежные доходы под 16,5 процентов годовых. Сравните современные значения полученных денежных доходов.
Решение.
Вычислим современные значения последовательностей денежных доходов по каждому проекту, дисконтируя ежегодные доходы при показателе дисконта 16,5%. Расчеты проведем с помощью специальных таблиц.
Проект 1 Таблица 1
| Год | Денежный поток | Множитель дисконта | Современное значение |
| 1 | $12,000 | ||
| 2 | $12,000 | ||
| 3 | $14,000 | ||
| 4 | $16,000 | ||
| Суммарное современное значение | |||
Проект 2 Таблица2
| Год | Денежный поток | Множитель дисконта | Современное значение |
| 1 | $10,000 | ||
| 2 | $14,000 | ||
| 3 | $16,000 | ||
| 4 | $14,000 | ||
| Суммарное современное значение | |||
По результатам расчетов можно сделать вывод о предпочтительности второго проекта.
7. Приведены данные о денежных потоках:
| Поток | Год | ||||
| 1 | 2 | 3 | 4 | 5 | |
| А | 100 | 200 | 200 | 300 | 300 |
| Б | 600 | — | — | — | — |
| В | — | — | — | — | 1200 |
| Г | 200 | — | 200 | — | 200 |
Рассчитайте для каждого потока показатели FV при r = 11,5% и PV при r = (11,5 3)% для двух случаев:
а) потоки имеют место в начале года;
б) потоки имеют место в конце года.
Решение
FV=100*(1 11,5)1 200*(1 11,5)2 200*(1 11,5)3 300*(1 11,5)4 300*(1 11,5)5=1250 31250 390625 732421 915527=$92,708,277
PV=100/(1 11,5 3)1 200/(1 11,5 3)2 200/(1 11,5 3)3 300/(1 11,5 3)4 300/(1 11,5 3)5 =0,645 0,832 0,054 0.051 0,0003353=$1,582.33
8. Анализируются два варианта накопления средств по схеме аннуитета (поступление денежных средств осуществляется в конце соответствующего временного интервала):
План 1: вносится вклад на депозит $500 каждые полгода при условии, что банк начисляет 9% годовых с полугодовым начислением процентов.
План 2: делается ежегодный вклад в размере $1000 на условиях (9 1)% годовых при ежегодном начислении процентов.
Определите:
а) какая сумма будет на счете через 10 лет при реализации каждого плана? Какой план более предпочтителен?
б) изменится ли ваш выбор, если процентная ставка в плане 2 будет снижена до (9-5)%?
Решение
А) определим будущую стоимость потока денежных средств через 10 лет
FV=PV*(1 r)n =$500*(1 0,9)10 =1183.6817/2(полгода)=$15.327,66
FV=PV*(1 r)n =$1000*(1 0,1)10 =$25.937,42
Предпочтительнее 2 план, тк при реализации этого плана сумма накапливается больше чем при реализации 1 плана
В) определим будущую стоимость потока денежных средств через 10 лет, если процентная ставка в плане 2 будет снижена до (9-0,5)%?
FV=PV*(1 r)n =$1000*(1 (9-5))10 =$1000*(1 0,4)10=$21.925,78
9. Каков ваш выбор — получение $5000 через год или $12000 через 6 лет, если коэффициент дисконтирования равен: а) 0%; б) 8,5%; в) (8,5 8)%?
Решение
Для случая а)
FV=PV*(1 r)n=$12000*(1 0)6=$12000
Выгоднее получить $5000 через год, чем $12000 через 6 лет при 0%
Для случая b)
FV=PV*(1 r)n=$12000*(1 8,5)6=$88210
Не Выгодно получать $5000 через год, когда можешь получить $88210 через 6 лет при 8,5%
Для случая B)
FV=PV*(1 r)n=$12000*(1 8,5 8)6=$344675
Получить $344675 через 6 лет при 8,5 8%
10. Предприятие требует как минимум 13 процентов отдачи при инвестировании собственных средств. В настоящее время предприятие располагает возможностью купить новое оборудование стоимостью $84,500. Использование этого оборудования позволит увеличить объем выпускаемой продукции, что в конечном итоге приведет к $17,000 дополнительного годового денежного дохода в течение 15 лет использования оборудования.
Решение.
Представим условия задачи в виде исходных данных.
Таблица
| Стоимость нового оборудования | $84500 |
| Время проекта | 15 лет |
| Остаточная стоимость | $2500 |
| Входной денежный поток за счет приобретения оборудования | $17000 |
| Показатель дисконта | 13% |
Расчет произведем с помощью следующей таблицы
Расчет значения NPV
Наименование денежного потока | Год(ы) | Денежный поток | Дисконтирование множителя 13%* | Настоящее значение денег |
Исходная инвестиция | Сейчас | $84,500 | 1 | $84,500 |
Входной денежный поток | 1-15 | $17000 | ||
| Современное чистое значение (NPV) | ||||
* Множитель дисконтирования определяется с помощью финансовых таблиц.
В результате расчетов NPV = $ > 0, и поэтому с финансовой точки зрения проект следует принять.
Сейчас уместно остановиться на интерпретации значения NPV. Очевидно, что сумма $ представляет собой некоторый “запас прочности”, призванный компенсировать возможную ошибку при прогнозировании денежных потоков. Американские финансовые менеджеры говорят — это деньги, отложенные на “черный день”.
11. Предприятие планирует новые капитальные вложения в течение трех лет: $90,000 в первом году, $70,000 — во втором и $50,000 — третьем. Инвестиционный проект рассчитан на 10 лет с полным освоением вновь введенных мощностей лишь на пятом году, когда планируемый годовой чистый денежный доход составит $75,000.
Необходимо определить
- чистое современное значение инвестиционного проекта,
- дисконтированный срок окупаемости.
Как изменится Ваше представление об эффективности проекта, если требуемый показатель отдачи составит (16,5 2)%.
Решение.
1. Определим чистые годовые денежные доходы в процессе реализации инвестиционного проекта:
в первый год — $75,000*0.4 = $30,000;
во второй год — $75,000*0.5 = $37,500;
в третий год — $75,000 *0.7 = $52,500;
в четвертый год — $75,000 *0.9 = $67,500;
во все оставшиеся годы — $75,000.
2Расчет чистого современного значения инвестиционного проекта произведем с помощью таблицы
Таблица
| Наименование денежного потока | Год(ы) | Денежный поток | Множитель дисконтирования | Настоящее значение денег |
| Инвестиция | Сейчас | ($90,000) | 1 | ($90,000) |
| Инвестиция | 1 | ($70,000) | ||
| Инвестиция | 1 | ($50,000) | ||
| Денежный доход | 1 | $30,000 | ||
| Денежный доход | 2 | $37,500 | ||
| Денежный доход | 3 | $52,500 | ||
| Денежный доход | 4 | $67,500 | ||
| Денежный доход | 5 | $75,000 | ||
| Денежный доход | 6 | $75,000 | ||
| Денежный доход | 7 | $75,000 | ||
| Денежный доход | 8 | $75,000 | ||
| Денежный доход | 9 | $75,000 | ||
| Денежный доход | 10 | $75,000 | ||
| Чистое современное значение инвестиционного проекта | ||||
3. Для определения дисконтированного периода окупаемости рассчитаем величины чистых денежных потоков по годам проекта. Для этого необходимо всего лишь найти алгебраическую сумму двух денежных потоков в первый год проекта. Она составит ($60,347) $16,035 = ($44,312). Остальные значения в последней колонке предыдущей таблицы представляют собой чистые значения.
- Расчет дисконтированного периода окупаемости произведем с помощью таблицы, в которой будем рассчитывать накопленный дисконтированный денежный поток по годам проекта.
Таблица
Год | Дисконтированный денежный поток | Накопленный денежный поток |
0 | ($120,000) | ($120,000) |
1 | ($44,312) | ($164,312) |
2 | $23,039 | ($141,273) |
3 | $27,806 | ($113,466) |
4 | $30,818 | ($82,648) |
5 | $29,518 | ($53,130) |
6 | $25,445 | ($27,685) |
7 | $21,936 | ($5,749) |
8 | $18,910 | $13,161 |
Из таблицы видно, что число полных лет окупаемости проекта составляет 7.
Дисконтированный срок окупаемости поэтому составит
года.
12. Предприятие имеет два варианта инвестирования имеющихся у него $200,000. В первом варианте предприятие вкладывает в основные средства, приобретая новое оборудование, которое через 6 лет (срок инвестиционного проекта) может быть продано за $14,000; чистый годовой денежный доход от такой инвестиции оценивается в $53,000.
Согласно второму варианту предприятие может инвестировать деньги частично ($40,000) в приобретение новой оснастки, а оставшуюся сумму в рабочий капитал (товарно-материальные запасы, увеличение дебиторских). Это позволит получать $,34000 годового чистого денежного дохода в течение тех же шести лет.
Какой вариант следует предпочесть, если предприятие рассчитывает на 13,5% отдачи на инвестируемые им денежные средства? Воспользоваться методом чистого современного значения.
Решение.
- Представим исходные данные задачи в компактном виде.
Таблица 34
| Проект | 1 | 2 |
| Инвестиции в основные средства………………… | $200,000 | — |
| Инвестиции в рабочий капитал…………………… | — | $200,000 |
| Годовой денежный доход……………………………. | $53,000 | $34,000 |
| Остаточная стоимость оборудования …………… | $14,000 | — |
| Высвобождение рабочего капитала……………… | — | $200,000 |
| Время проекта……………………………………………. | 6 лет | 6 лет |
Заметим еще раз, что рабочий капитал и оборудование планируются быть реализованными только по истечении 6 лет.
- Произведем расчеты чистого современного значения для первого проекта.
Таблица 35
| Наименование денежного потока | Год(ы) | Денежный поток | Множитель дисконтирования | Настоящее значение денег |
| Инвестиция | Сейчас | ($200,000) | 1.000 | ($200,000) |
| Денежный доход | 1-6 | $53,000 | ||
| Продажа оборудов. | 6 | $14,000 | ||
| Чистое современное значение | ||||
- Аналогичные расчеты проведем для второго проекта
Таблица 36
| Наименование денежного потока | Год (ы) | Денежный поток | Множитель дисконтирования | Настоящее значение денег |
| Инвестиция | Сейчас | ($200,000) | 1.000 | ($200,000) |
| Денежный доход | 1-6 | $24,000 | ||
| Высвобождение | 6 | $200,000 | ||
| Чистое современное значение | ||||
4. По результатам расчетов можно сделать следующие выводы:
- лучшим следует признать второй проект;
- первый проект вообще следует отклонить даже без связи с имеющейся альтернативой.
13. Предприятие рассматривает инвестиционный проект, предусматривающий приобретение основных средств и капитальный ремонт оборудования, а также вложения в оборотные средства по следующей схеме:
- $95,000 — исходная инвестиция до начала проекта;
- $15,000 — инвестирование в оборотные средства в первом году;
- $10,000 — инвестирование в оборотные средства во втором году;
- $10,000 — инвестирование в оборотные средства в третьем году;
- $8,000 — дополнительные инвестиции в оборудование на пятом году;
- $7,000 — затраты на капитальный ремонт на шестом году;
В конце инвестиционного проекта предприятие рассчитывает реализовать оставшиеся основные средства по их балансовой стоимости $15,000 и высвободить оборотные средства.
Результатом инвестиционного проекта должны служить следующие чистые (т.е. после уплаты налогов) денежные доходы:
| 1 год | 2 год | 3 год | 4 год | 5 год | 6 год | 7 год | 8 год |
| $15,000 | $25,000 | $30,000 | $40,000 | $40,000 | $40,000 | $30,000 | $20,000 |
Необходимо рассчитать чистое современное значение инвестиционного проекта и сделать вывод о его эффективности при условии 13,5 процентной требуемой прибыльности предприятия на свои инвестиции.
Решение.
Составляем таблицу расчетных данных и определяем дисконтированные значения всех денежных потоков.
Проект следует принять, поскольку его чистое современное значение существенно положительное.
Таблица
| Наименование денежного потока | Год | Денежный | Множитель дисконта | Настоящее |
| Приобретение основных средств | 0 | ($95,000) | 1 | ($95,000) |
| Инвестирование в оборотные средства | 1 | ($15,000) | ||
| Денежный доход в первый год | 1 | $15,000 | ||
| Инвестирование в оборотные средства | 2 | ($10,000) | ||
| Денежный доход во второй год | 2 | $25,000 | ||
| Денежный доход в третий год | 3 | $10,000 | ||
| Денежный доход в четвертый год | 4 | $40,000 | ||
| Приобретение основных средств | 4 | ($15,000) | ||
| Денежный доход в пятый год | 5 | $8,000 | ||
| Ремонт оборудования | 6 | ($7,000) | ||
| Денежный доход в шестой год | 6 | $40,000 | ||
| Денежный доход в седьмой год | 7 | $30,000 | ||
| Денежный доход в восьмой год | 8 | $20,000 | ||
| Продажа оборудования | 8 | $15,000 | ||
| Высвобождение оборотных средств | 8 | $35,000 | ||
| Чистое современное значение | ||||
14. Проект, требующий инвестиций в размере $160000, предполагает получение годового дохода в размере $30000 на протяжении 15 лет. Оцените целесообразность такой инвестиции, если коэффициент дисконтирования – 13,5%.
Решение
По условию задачи Проект требует инвестиций в размере $160000 в течение 15 лет. Для определения суммы накопленных денег необходимо вычислить будущее значение 15-летнего аннуитета при процентной ставке наращения 13,5 процентов. Используем формулу будущего значения аннуитета:
FV=CF*Znk=1(1 r) n-k =$30,000*Z15k=1(1 13, 5) n-k =$907500
15. Проект, рассчитанный на 15 лет, требует инвестиций в размере $150000. В первые 5 лет никаких поступлений не ожидается, однако в последующие 10 лет ежегодный доход составит $50000. Следует ли принять этот проект, если коэффициент дисконтирования равен 13%?
Решение
Рассчитаем, каковы будут поступления в течение 10 лет при 13%
F=P*(1 r) n=$50000*(1 0, 13)10=$169728, 35
16. Анализируются проекты ($):
| IC | C1 | C2 | |
| А | -4000 | 2500 | 3000 |
| Б | -2000 | 1200 | 1500 |
Ранжируйте проекты по критериям IRR, NPV, если r = 13%.
Решение
NPV для проекта А
NPV=-4000/(1 0,13)1 2500/(1 0,13)2 3000/(1 0,13)3=-3539.82 1957.86 2079,29=$436,8
В результате расчетов NPV = $436,8 > 0, и поэтому с финансовой точки зрения проект следует принять.
NPV для проекта В
NPV=-2000/(1 0,13)1 1200/(1 0,13)2 1500/(1 0,13)3=$209,5
В результате расчетов NPV = $209,5 > 0, и поэтому с финансовой точки зрения проект следует принять.
17. Для каждого из нижеприведенных проектов рассчитайте NPV и IRR, если значение коэффициента дисконтирования равно 16%.
| А | -370 | — | — | — | — | 1000 |
| В | -240 | 60 | 60 | 60 | 60 | — |
| С | -263,5 | 100 | 100 | 100 | 100 | 100 |
18. Сравните по критериям NPV, IRR два проекта, если стоимость капитала 16%:
| А | -20000 | 7000 | 7000 | 7000 | 7000 |
| Б | -25000 | 2500 | 5000 | 10000 | 20000 |
Решение
NPV для проекта А
NPV=20000/(1 0,16)1 7000/(1 0,16)2 7000/(1 0,16)3 7000/(1 0,16)4 7000/(1 0,16)5 =-1724,13 5202,14 4484,87 1068,11 3332,83=$15812,08
В результате расчетов NPV = $15812,08 > 0, и поэтому с финансовой точки зрения проект следует принять.
NPV для проекта В
NPV=25000/(1 0,16)1 2500/(1 0,16)2 5000/(1 0,16)3 10000/(1 0,16)4 20000/(1 0,16)5 =-21551,7 1857.9 3203,48 5523,03 9522,4=$-1444,89
получим NPV = $-1444,89 то есть критерий является отрицательным и проект следует отклонить.
исходная инвестиция не окупается, т.е. положительные денежные потоки, которые генерируются этой инвестицией не достаточны для компенсации, с учетом стоимости денег во времени, исходной суммы капитальных вложений.
19. Величина требуемых инвестиций по проекту равна $18000; предполагаемые доходы: в первый год — $1500, в последующие 8 лет по $3600 ежегодно. Оцените целесообразность принятия проекта, если стоимость капитала 10%.





