Прибавить и отнять процент в Excel от числа с примерами

Расчет первоначального значения с учетом процента изменения.

Например, вам предложили купить пылесос за 200 долларов, что на 40% ниже первоначальной цены. Вы хотите узнать, какова была первоначальная цена.

Поскольку 40% – это скидка, вы сначала вычитаете ее из 100%, чтобы узнать, какой процент вы действительно должны заплатить (100% — 40% = 60%). Теперь вам нужна формула для расчета исходной цены, то есть для определения числа, 60% которого равняется 200.

Формула выглядит следующим образом:

Число / Процент = Результат

Применительно к скидке от первоначальной цены в 40% можно применять любую из следующих формул:

=A2/(100%-B2) или =A2/(1-B2) или =A2/0.6 или =A2/60%

EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент

Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.

Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.

Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.

XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора

Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.

Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.

RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам

Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.

Вариант 1: расчет процентов от числа

Прежде всего давайте выясним, как рассчитать величину доли в процентах одного числа от другого.

1. Формула вычисления выглядит следующим образом: =(число)/(общая_сумма)*100%.
2. Чтобы продемонстрировать вычисления на практике, узнаем, сколько процентов составляет число 9 от 17. Выделяем ячейку, куда будет выводиться результат и обязательно обращаем внимание, какой формат указан на вкладке «Главная» в группе инструментов «Число». Если формат отличен от процентного, обязательно устанавливаем в поле параметр «Процентный».
3. После этого записываем следующее выражение: =9/17*100%.



4. Впрочем, так как мы задали процентный формат ячейки, дописывать значение «*100%» не обязательно. Достаточно ограничиться записью «=9/17».



5. Чтобы посмотреть результат, жмем на клавишу Enter. В итоге получаем 52,94%.

Теперь взглянем, как можно вычислять проценты, работая с табличными данными в ячейках.

1. Допустим, нам требуется посчитать, сколько процентов составляет доля реализации конкретного вида товара от общей суммы, указанной в отдельной ячейке. Для этого в строке с наименованием товара кликаем по пустой ячейке и устанавливаем в ней процентный формат. Ставим знак «=». Далее щелкаем по клеточке с указанием величины реализации конкретного вида товара «/». Потом — по ячейке с общей суммой реализации по всем товарам. Таким образом, в ячейке для вывода результата у нас записана формула.



2. Чтобы посмотреть значение вычислений, нажимаем Enter.



3. Мы выяснили определение доли в процентах только для одной строки. Неужели для каждой следующей строки нужно будет вводить подобные вычисления? Совсем не обязательно. Нам надо скопировать данную формулу в другие ячейки. Однако поскольку при этом ссылка на ячейку с общей суммой должна быть постоянной, чтобы не происходило смещение, то в формуле перед координатами ее строки и столбца ставим знак «$». После этого ссылка из относительной превращается в абсолютную.



4. Наводим курсор в нижний правый угол ячейки, значение которой уже рассчитано, и, зажав кнопку мыши, тянем ее вниз до ячейки, где располагается общая сумма включительно. Как видим, формула копируется и на все другие клетки таблицы. Сразу виден результат подсчетов.



5. Можно посчитать процентную долю отдельных составляющих таблицы, даже если итоговая сумма не выведена в отдельную ячейку. После форматирования ячейки для вывода результата в процентный формат ставим в ней знак «=». Далее кликаем по ячейке, чью долю надо узнать, ставим знак «/» и набираем сумму, от которой рассчитывается процент. Превращать ссылку в абсолютную в этом случае не нужно.



6. Затем жмем Enter и путем перетягивания копируем формулу в ячейки, которые расположены ниже.

Вариант 2: расчет числа по проценту

Теперь посмотрим, как рассчитать число от общей суммы по проценту от нее.

1. Формула для расчета будет иметь следующий вид: величина_процента%*общая_сумма. Следовательно, если нам понадобилось посчитать, какое число составляет, например, 7% от 70, то просто вводим в ячейку выражение «=7%*70». Так как в итоге мы получаем число, а не процент, то в этом случае устанавливать процентный формат не надо. Он должен быть или общий, или числовой.



2. Для просмотра результата нажмите Enter.



3. Эту модель довольно удобно применять и для работы с таблицами. Например, нам нужно от выручки каждого наименования товара подсчитать сумму величины НДС, которая составляет 18%. Для этого выбираем пустую ячейку в строке с наименованием товара. Она станет одним из составных элементов столбца, в котором будут указаны суммы НДС. Форматируем ее в процентный формат и ставим в ней знак «=». Набираем на клавиатуре число 18% и знак «*». Далее кликаем по ячейке, в которой находится сумма выручки от продажи данного наименования товара. Формула готова. Менять формат ячейки на процентный или делать ссылки абсолютными не следует.



4. Для просмотра результата вычисления жмем Enter.



5. Копируем формулу в другие ячейки перетаскиванием вниз. Таблица с данными о сумме НДС готова.

Как видим, программа предоставляет возможность удобно работать с процентными величинами. Пользователь может вычислить как долю от определенного числа в процентах, так и число от общей суммы по проценту. Excel можно использовать для работы с процентами как обычный калькулятор, но также с его помощью легко и автоматизировать работу по вычислению процентов в таблицах.

Вычисление наращенной суммы при переменной процентной ставке

При установлении переменной процентной ставки, т.е. дискретно изменяющейся во времени ставки, наращенная ставка определяется по формуле:

В

файле примера

на листе

Переменная ставка

сделаны расчеты по этой формуле: =

C7*(1 СУММПРОИЗВ(A12:A14;B12:B14))

В случае, если процентная ставка изменяется через равные периоды, то вышеуказанную формулу можно несколько упростить.

n – период действия ставки без изменения.

Вычисление наращенной суммы при постоянной процентной ставке

Вышеуказанная формула простых процентов настолько проста, что не понятно, в чем вообще состоит проблема вычислений? Вычислить

Наращенную сумму

S

при известных Р, n, i или вычислить i при известных  Р, n, S можно и на калькуляторе. Однако, все несколько усложняется в случае, когда срок финансовой сделки не равен целому числу лет.

Если срок предоставления кредита определен в месяцах, то формулу для определения наращенной суммы необходимо изменить, разделив годовую ставку i на 12 (12 месяцев в году). Под n теперь будем понимать количество месяцев. S=P*(1 n*i/12) i/12 – это ставка за период (за месяц).

Если срок финансовой сделки определен в кварталах, то под n будем понимать количество кварталов, на который был выдан кредит (или заключен договор срочного вклада). Годовую ставку i нужно разделить на 4 (4 квартала в году). Формула выглядит так: S=P*(1 n*i/4)

По аналогии, можно предположить, что если срок финансовой сделки определен в днях, то под n разумно понимать количество дней, на который был выдан кредит. Однако со ставкой за период не все так просто. Действительно, i нужно делить на 365 (365 дней в году)

где t — число дней функционирования сделки (число дней, на которое предоставили кредит); К — временная база (число дней в году).

Временную базу года можно брать число дней в году (365 или 366), или даже 360. Откуда 360? Дело в том, что в ряде стран для удобства вычислений год делится на 12 месяцев, по 30 дней в каждом, т.е. продолжительность года

К

принимается равной 360 дням (12*30).

В этой связи различают три метода процентных расчетов, зависимых от выбранного периода начисления.

1. Точные проценты с точным числом дней ссуды (английский (британский) метод). При этом методе продолжительность года К принимается равной 365 (или 366) дням и определяется фактическое число дней t между двумя датами (датой получения и погашения кредита), т.е. временная база – календарный год.

Примечание

.

Вычисление по формуле S=P*(1 n*i/365) является лишь приблизительным по английскому методу в случае високосного года (см. ниже).

2. Обыкновенные (обычные) проценты с точным числом дней ссуды (французский метод, банковское правило, гибридный метод). При этом методе величина t рассчитывается, как и в предыдущем методе, а продолжительность года принимается равной К = 360 дням (коммерческий год, обыкновенный год). Это позволяет французским банкирам зарабатывать в 1,01388 раза больше денег, чем английским (365/360= 1,01388) за тот же период.

Примечание

.

Вычисление по французскому методу можно производить по формуле S=P*(1 n*i/360), где i – годовая ставка, n – число дней ссуды.

3. Обыкновенные проценты с приближенным числом дней ссуды (германский метод). При этом методе величина t определяется так:
   
   количество полных месяцев
   
   ссуды *умноженное на 30 дней в каждом точное число дней ссуды в неполных месяцах; продолжительность года К = 360 дней.

В

файле примера

приведен расчет начисления процентов по 3-м методам.

Примечание

.

При точном и приближенном методах начисления процентов день выдачи и день погашения ссуды принимаются за 1 день.

Понятно, что вычисления по английской и германской системе могут быть сделаны, только если заданы конкретная дата выдачи кредита и дата окончания его срока. Т.к. чтобы вычислить по английской системе – требуется знать продолжительность конкретного года (високосный или нет), а по немецкой – требуется знать количество полных месяцев и число дней ссуды в неполных месяцах.

По французскому методу количество дней ссуды берется фактическое, а временная база всегда =360, поэтому вычисления производить можно и без знания конкретных дат (достаточно знать количество дней ссуды). Еще одно замечание о вычислении наращенной суммы при использовании английского метода.

Напомним, что продолжительность года в этом методе принимается равной 365 (или 366) дней, правда, не всегда понятно как проводить вычисления, если срок кредита приходится и на високосный и обычный год (например, кредит выдан 31.10.2022, а должен быть погашен в 15.06.

2022, високосный 2022). Т.к. в РФ используется английский метод, то ЦЕНТРАЛЬНЫЙ БАНК РОССИЙСКОЙ ФЕДЕРАЦИИ опубликовал письмо от 27 декабря 1999 г. N 361-Т для разъяснения этой ситуации:

В случае, если дни периода начисления процентов по привлеченным (размещенным) банками денежным средствам приходятся на календарные годы с разным количеством дней (365 и 366 дней соответственно), то начисление процентов за дни, приходящиеся на календарный год с количеством дней 365, производится из расчета 365 календарных дней в году, а за дни, приходящиеся на календарный год с количеством дней 366, производится из расчета 366 календарных дней в году.

В

файле примера

в ячейке

В50

приведена

формула массива

, которая позволяет вычислить наращенную сумму в случае кредита, когда года даты выдачи и даты погашения ссуды не совпадают (например, кредит выдан 31.03.2022, а должен быть погашен в 15.06.2022).

Вычисляем ставку сложных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. с ежегодным начислением сложных процентов. При какой годовой ставке сумма вклада удвоится через 5 лет?

В

файле примера

приведено решение, ответ 14,87%.

Примечание

. Об эффективной ставке процентов

читайте в этой статье

.

Как всё посчитать

Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.

Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.

Как посчитать маржу в процентах.

Прежде всего, давайте определим разницу между понятиями наценки и маржи.

По абсолютному значению (в денежных единицах) они одинаковы. Рассчитываются они как разность между себестоимостью (или закупочной ценой) и ценой реализации товара.

А вот в процентах они совершенно разные.

Наценка всегда рассчитывается в процентах к себестоимости или цене закупки товара. Размер ее может быть от нуля до бесконечности (хоть 1000% накручивай, если купят).

%наценки = (цена – себестоимость)/себестоимость

Маржа показывает долю дохода в цене. Поэтому она должна быть больше 0, и всегда меньше 100%.

%маржи = (цена – себестоимость)/цена

Воспользуемся примером:

Как видите, уровень процентов наценки и маржи могут очень сильно отличаться.

Но при этом они связаны. Поэтому, к примеру, если мы знаем процент наценки, то легко посчитать маржу.

Если мы продали товара на 1000 рублей и применяли при этом наценку в 30%, то отсюда мы сначала можем найти себестоимость товара:

=сумма продаж / (100% %наценки)

1000/(100% 30%)=769,23

Считаем маржу:

1000 – 769,23 = 230,77

Маржа в процентах: 230,77/1000 = 23,08%

А теперь как посчитать наценку, если знаем маржу? Используем те же цифры.

Сумма продаж  — 1000 руб. Маржа – 230,77 руб.

Отсюда себестоимость 1000 – 230,77 = 769,23 руб.

Процент наценки 230,77/769,23 = 30%

Эти несколько примеров применения процентов, надеюсь, будут полезны. Если у вас есть вопросы – пишите в комментариях.

Как посчитать наценку в процентах.

Предположим, товар стоит 100 рублей. Мы знаем также, что на него была сделана наценка 10 рублей. Как посчитать эту наценку в процентах?

Ответ  «10 процентов» будет неверным. В данном случае нельзя просто взять процент от итоговой цены. Ведь наценку мы делаем на первоначальную цену без наценки.

Принимаем итоговую цену за 100%. Тогда первоначальная цена будет составлять на 10% меньше, то есть 90%. В итоге формула расчета процента наценки будет такая:

=наценка / (цена — наценка) * 100%

А теперь запишем это на листе Excel:

Здесь у нас нет необходимости умножать на 100%, а просто применяем к ячейке C2 процентный формат:

=B2/(A2-B2)

Вы можете проверить расчёт: добавьте к 90 рублям 11,1% и получите как раз 100.

Как посчитать разницу в процентах в excel?

Насколько изменилось значение между двумя величинами в процентах.

Сначала абстрагируемся от Excel. Месяц назад в магазин привозили столы по цене 100 рублей за единицу. Сегодня закупочная цена – 150 рублей.

Разница в процентах = (новые данные – старые данные) / старые данные * 100%.

В нашем примере закупочная стоимость единицы товара увеличилась на 50%.

Посчитаем разницу в процентах между данными в двух столбцах:

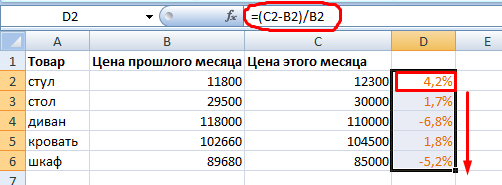
Не забываем выставлять «Процентный» формат ячеек.

Рассчитаем процентное изменение между строками:

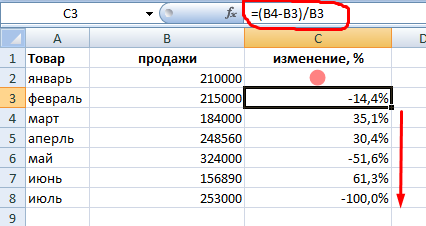
Формула такова: (следующее значение – предыдущее значение) / предыдущее значение.

При таком расположении данных первую строку пропускаем!

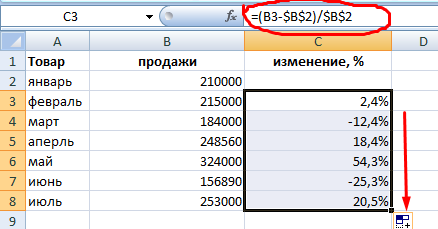
Если нужно сравнить данные за все месяцы с январем, например, используем абсолютную ссылку на ячейку с нужным значением (знак $).

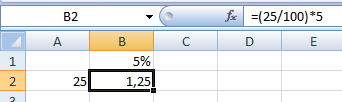
Как прибавить процент к числу

Задача решается в два действия:

1. Находим, сколько составляет процент от числа. Здесь мы вычислили, сколько будет 5% от 25.



2. Прибавим результат к числу. Пример для ознакомления: 25 5%.

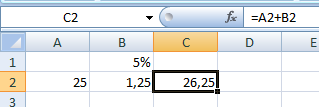
А здесь мы выполнили собственно сложение. Опустим промежуточное действие. Исходные данные:

Ставка НДС – 18%. Нам нужно найти сумму НДС и прибавить ее к цене товара. Формула: цена (цена * 18%).

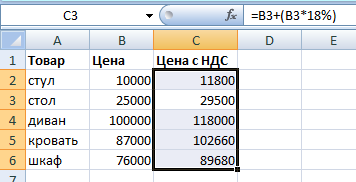
Не забываем про скобки! С их помощью устанавливаем порядок расчета.

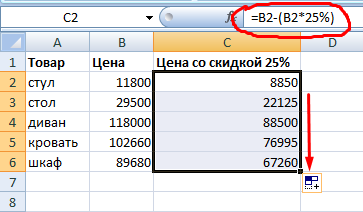
Чтобы отнять процент от числа в Excel следует выполнить такой же порядок действий. Только вместо сложения выполняем вычитание.

Как сделать диаграмму с процентами

Первый вариант: сделать столбец в таблице с данными. Затем использовать эти данные для построения диаграммы. Выделяем ячейки с процентами и копируем – нажимаем «Вставка» — выбираем тип диаграммы – ОК.

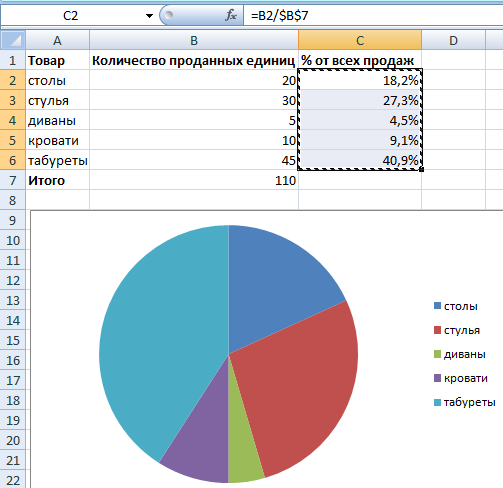
Второй вариант: задать формат подписей данных в виде доли. В мае – 22 рабочих смены. Нужно посчитать в процентах: сколько отработал каждый рабочий. Составляем таблицу, где первый столбец – количество рабочих дней, второй – число выходных.

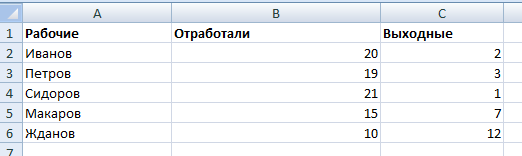
Делаем круговую диаграмму. Выделяем данные в двух столбцах – копируем – «Вставка» — диаграмма – тип – ОК. Затем вставляем данные. Щелкаем по ним правой кнопкой мыши – «Формат подписей данных».

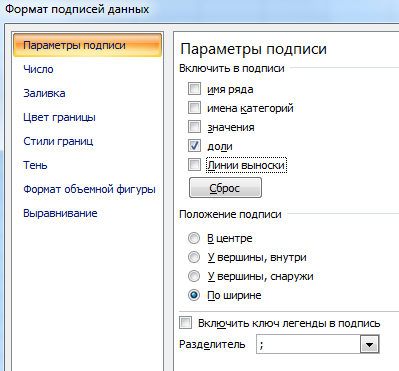
Выбираем «Доли». На вкладке «Число» — процентный формат. Получается так:

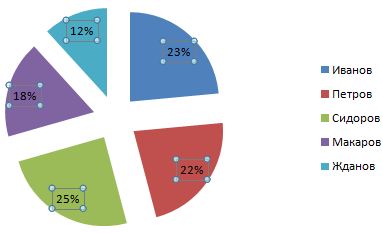
Как увеличить или уменьшить весь столбец на процент.

Предположим, у вас есть столбец чисел, который вы хотите увеличить или уменьшить на определенный процент. Вы также хотите, чтобы обновленные числа были в том же столбце, а не добавлять новый столбец с формулами.

Вот пошаговая инструкция для решения этой задачи:

1. Введите все числа, которые вы хотите увеличить или уменьшить, в какой-нибудь столбец (столбец А в этом примере).
2. В пустой ячейке введите одну из следующих формул:

Число увеличиваем на процент: =1 40%

Число минус процент: =1 — 40%

Естественно, вы можете заменить 40% в приведенных выше формулах любым нужным процентом.

3. Выделите ячейку с формулой (в нашем случае C1) и скопируйте ее, нажав Ctrl C.
4. Выберите диапазон ячеек, который нужно изменить, щелкните выделение правой кнопкой мыши и выберите «Специальная вставка…»
5. В открывшемся диалоговом окне выберите «Значения» и «Умножить», нажмите «ОК».

И вот результат – все выбранные числа в столбце А умножены на 40%.

Таким же образом вы можете разделить столбец чисел на определенный процент. Просто введите нужное число в пустую ячейку и следуйте инструкциям выше. В Специальной вставке вместо «умножить» выберите «разделить».

Как умножить число на процент.

Часто бывает необходимо умножить число какой-то процент. К примеру, речь идет об изменении текущей цены через какой-то промежуток времени (например, через месяц), чтобы добавить к ней определенный процент.

Чтобы увеличить число на определённый процент, используйте эту формулу:

= Число * (1 %)

или

= Число * (100% %)

Например, формула =A1*(1 20%) увеличивает значение в ячейке A1 на 20%.

Чтобы уменьшить на процент:

= Число * (1 — %)

Например, формула =A1*(1-20%) уменьшает значение в ячейке A1 на 20%.

В нашем примере, если A2 – действующая цена, а B2 — процент, на который вы ожидаете её увеличение либо уменьшение, то вот формулы, которые вы должны ввести в ячейку C2:

Умножить на процент: =A2*(1 B2)

Уменьшить на процент: =A2*(1-B2)

Кроме того, как вы видите на рисунке выше, процент может быть выражен и отрицательным числом, что означает уменьшение первоначального значения. В этом случае формула =A2*(1 B2) также отлично подходит.

Какие данные нужны

Формула состоит из трёх компонентов:

=ЧИСТНЗ(ставка;значения;даты)

Второй и третий достаточно ясны:

2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.3. Даты — когда именно средства приходят или уходят.

Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.

Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру, ОФЗ 26234 — 4,5%.

Определяем сумму начисленных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. на 5 лет с ежегодным начислением сложных процентов по ставке 12 % годовых. Определить сумму начисленных процентов.

Сумма начисленных процентов I равна разности между величиной  наращенной суммы S и начальной суммой Р. Используя формулу для определения наращенной суммы S = Р*(1 i )^n, получим: I = S – P= Р*(1 i)^n – Р=P*((1 i)^n –1)=150000*((1 12%)^5-1) Результат: 114 351,25р.

Сколько составляет процент от числа.

Предположим, вы покупаете новый телевизор за 800 долларов, и за доставку с вас просят 4% от стоимости покупки. Вопрос в том, сколько вы должны заплатить сверх первоначальной цены? Другими словами, что составляет 4% от 800 долларов?

Поможет следующая формула:

Число * Процент = Результат

Предполагая, что цена записана в ячейке A2, а процент — в B2, приведенная выше формула превращается в =A2*B2 и возвращает 32.

Помните, что когда вы записываете в таблицу число, за которым следует знак процента (%), то оно интерпретируется Excel как сотая часть его значения (то есть, сразу делится на 100). Например, 4% фактически сохраняется как 0,04, и Excel использует это значение во всех формулах и расчетах.

Другими словами, формула =A2*11% эквивалентна =A2*0.11. Естественно, вы можете использовать десятичное число, соответствующее процентному соотношению, непосредственно в формуле, если это лучше подходит для ваших таблиц.

Учет (дисконтирование) по сложным процентам

Дисконтирование основывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Рассмотрим 2 вида учета: математический и банковский.

Математический учет

. В этом случае решается задача обратная наращению по сложным процентам, т.е. вычисления производятся по формуле Р=S/(1 i )^n Величину Р, полученную дисконтированием S, называют современной, или текущей стоимостью, или приведенной величиной S.

Пример

. Через 7 лет страхователю будет выплачена сумма 2000000 руб. Определить современную стоимость суммы при условии, что применяется ставка сложных процентов в 15% годовых. Другими словами, известно: n = 7 лет, S = 2 000 000 руб., i = 15% .

Решение. P = 2000000/(1 15% )^7 Значение текущей стоимости будет меньше, т.к. открыв

сегодня

вклад на сумму Р с ежегодной капитализацией по ставке 15% мы получим через 7 лет сумму 2 млн. руб.

Тот же результат можно получить с помощью формулы

=ПС(15%;7;;-2000000;1)

Функция

ПС()

возвращает приведенную (к текущему моменту) стоимость инвестиции и

рассмотрена здесь

.

Банковский учет

. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле: Р = S*(1- dсл )^n где dcл — сложная годовая учетная ставка.

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.

Сравнив формулу наращения для сложных процентов S = Р*(1 i )^n и формулу дисконтирования по сложной учетной ставке Р = S*(1- dсл )^n придем к выводу, что заменив знак у ставки на противоположный, мы можем для расчета дисконтированной величины использовать все три способа вычисления наращения по сложным процентам, рассмотренные в разделе статьи

Начисление процентов несколько раз в год

.